Licht [lat. Lux, zu grch. leukos >\veiß<, >glänzend<], die durch das Auge und andere Lichtsinnesorgane vermittelte Empfindung der Helligkeit. Mit diesem aussagestarken Satz beginnt der vielzitierte ‘Große Brockhaus’ seinen Artikel über das Licht. Uns soll natürlich weniger interessieren, was Licht ist, als wie es sich verhält -wodurch es zum Aussehen unserer Umgebung beiträgt.
Was ist es überhaupt, worauf unser Auge zu reagieren vermag, was uns eine Empfindung von Helligkeit vermittelt? Im allgemeinen geht man davon aus, daß das Auge auf elektromagnetische Wellen von ca. 0.4-0.75 um anspricht, entsprechend den Farbempfindungen violett bis rot. Das Auge besitzt dazu eine große Anzahl von Empfängerzellen, die sich in zwei Typen unterscheiden lassen: Ca. 75-150 Millionen Zellen reagieren nur auf Helligkeit, weitgehend unabhängig von der Lichtfrequenz, während sich ungefähr 6 Millionen Zellen mit dem Erkennen von Farben befassen. Die Schwarz/Weiß-Empfänger sind erheblich empfindlicher, weshalb Menschen im Halbdunkel nur Schwarz/Weiß sehen und erst bei ausreichender Beleuchtung auch Farben unterscheiden können. In brauchbarer Näherung ist die Empfindlichkeit des Auges logarithmisch.
 Bild 1: Optische Täuschungen. Die graue Fläche in der Mitte hat in beiden Feldern die gleiche Helligkeit. Trotzdem erscheint sie dunkler, wenn sie von einem hellen Rand umgeben wird. Dies ist eine Folge der Kontrastmittelung des Auges.
Bild 1: Optische Täuschungen. Die graue Fläche in der Mitte hat in beiden Feldern die gleiche Helligkeit. Trotzdem erscheint sie dunkler, wenn sie von einem hellen Rand umgeben wird. Dies ist eine Folge der Kontrastmittelung des Auges.
Sehen beruht also darauf, daß Lichtwellen an unser Auge kommen, Lichtwellen, die dazu, wie jeder aus eigener Erfahrung weiß, ganz offensichtlich zuerst einmal von einer Lichtquelle ausgesandt werden müssen. Wir sehen dann den Teil des Lichtes, das entweder auf dem direkten Wege oder über Reflexion an irgendwelchen Körpern unser Auge erreicht. Genauso offensichtlich ist. daß das Licht nicht von allen Körpern gleichartig reflektiert wird - denn das verschiedenartige Aussehen zweier von der gleichen Lichtquelle beleuchteter Körper läßt sich kaum anders als durch unterschiedliche Reflexionseigenschaften erklären. Damit sind wir auch gleich beim Phänomen Farbe angelangt. Aus dem Physikunterricht werden die meisten Leser noch wissen, daß Licht eine Farbe besitzt, oder daß weißes Licht sich mit Hilfe eines Prismas in verschiedenfarbige Anteile aufspalten läßt. Um es kurz zu machen, weiß empfindet man Licht, das alle sichtbaren Lichtfrequenzen in ungefähr gleicher Intensität enthält, ansonsten hat das Licht die Farbe des Anteils oder der Anteile, die am stärksten vertreten sind. Bei der Reflexion von Licht an einem Körper entsteht der Farbeindruck dadurch, daß bestimmte Lichtanteile stärker als andere reflektiert werden. Die Farbtheorie ist zwar nicht ganz so einfach, wie es diese Erklärung erscheinen läßt, für unsere Zwecke genügt es aber zu wissen, daß sich jede Farbe statt aus allen sichtbaren Frequenzen auch aus den drei sogenannten Primärfarben Rot, Grün und Blau zusammenmischen läßt, vorausgesetzt, man addiert ihre Intensitäten - sogenannte additive Mischung (Im Gegensatz zum Farbenmischen mit dem Malkasten - dort werden Intensitäten reduziert, denn jede Farbe, die man dazumischt, filtert einen Anteil der Beleuchtung heraus - subtraktive Mischung). Mischt man Licht der drei Primärfarben mit gleicher Intensität zusammen, erscheint das Licht weiß, wenn man die Intensitäten gleichmäßig reduziert grau und grauer und schließlich schwarz. Wenn man die Primärfarben mit unterschiedlichen Intensitäten mischt, kann jede gewünschte Farbe entstehen. Nach genau diesem Prinzip werden die Farben auch beim Atari ST gemischt, da aber nur 512 Farbtöne zur Verfügung stehen, ist die Anzahl der möglichen Intensitätsstufen für jede Grundfarbe beschränkt. Es gibt auch noch andere Mischsysteme, die meisten sind jedoch weniger leicht verständlich und anschaulich als das RGB-System. Da es auch das meistverwandte ist, wollen wir uns darauf beschränken. Auch Fernsehkameras arbeiten übrigens auf diese Weise: Je eine Bildröhre empfängt rote, blaue und grüne Lichtanteile, der Fernseher setzt das Bild dann auch wieder aus Punkten in diesen drei Grundfarben, die mit unterschiedlicher Intensität von der Bildröhre angeregt werden können, zusammen.
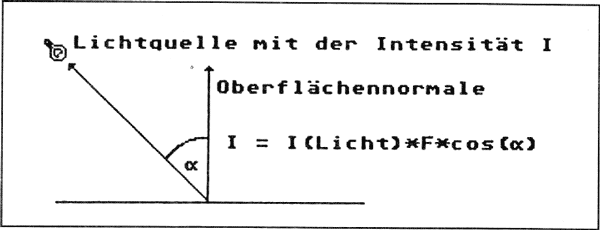 Bild 2: Die Oberflächenhelligkeit eines perfekt diffusen Reflektors ergibt sich aus dem Lichteinfallswinkel zur Oberflächennormalen: IFläche=ILicht * F * cos( a). Dabei ist F der Faktor, der die diffuse Reflektionsfähigkeit der Oberfläche beschreibt. Zur Erinnerung: Diffuse Reflektion bedeutet, daß Licht, das aus einer bestimmten Richtung auftrifft, gleichmäßig in alle Richtungen reflektiert wird.
Bild 2: Die Oberflächenhelligkeit eines perfekt diffusen Reflektors ergibt sich aus dem Lichteinfallswinkel zur Oberflächennormalen: IFläche=ILicht * F * cos( a). Dabei ist F der Faktor, der die diffuse Reflektionsfähigkeit der Oberfläche beschreibt. Zur Erinnerung: Diffuse Reflektion bedeutet, daß Licht, das aus einer bestimmten Richtung auftrifft, gleichmäßig in alle Richtungen reflektiert wird.
Darüber, wie viele Farbtöne das Auge überhaupt wahrnehmen kann, sind verschiedene Quellen oft sehr unterschiedlicher Meinung, was auch verständlich ist, da man solche Ergebnisse ja nur empirisch und unter verschiedensten Voraussetzungen erhalten kann. Jedenfalls schwanken die mir bekannten Angaben zwischen 5 und 25 Millionen erkennbaren Farbtönen. Vermutlich dürfte die Zahl erheblich niedriger sein, wenn man die Farben im A/B-Vergleich sieht und höher, wenn Unregelmäßigkeiten in Farbverläufen erkannt werden sollen.
Schließlich spielen im menschlichen Sehen noch einige andere Faktoren mit, die sich unter dem Begriff ‘optische Täuschungen’ zusammenfassen lassen. Nicht immer erscheint uns etwas so, wie es in den ‘Augen’ eines Intensitätsmeßgerätes aussieht. Zum Beispiel sieht ein Feld mittlerer Helligkeit unterschiedlich hell aus, je nachdem, ob es von einem schwarzen oder weißen Rand umgeben ist (Bild 1). Der Grund für solche Erscheinungen ist, daß sich das Auge an die mittlere Helligkeit einer Szene anpaßt. Die mittlere Helligkeit einer grauen Fläche mit schwarzem Rand ist aber niedriger, als die mittlere Helligkeit der gleichen grauen Fläche, wenn sie von einem weißen Rand umgeben ist.
Derartige Täuschungen gibt es zu viele, als daß sie hier alle aufgezählt werden könnten. Das Beispiel mag genügen.
Das Aussehen eines Körpers läßt sich mit Hilfe seiner Reflexionseigenschaften beschreiben. Allerdings wird nicht nur die Farbe einer Oberfläche von diesen Eigenschaften bestimmt. Stellen wir uns zuerst einmal vor, der ganze Raum sei von einer indirekten Lichtquelle beleuchtet, und zwar völlig gleichmäßig. Die Fläche wird dann einen Teil des Umgebungslichtes reflektieren und zwar völlig unabhängig von der Oberflächenrauhheit, wenn die Umgebungshelligkeit gleichmäßig genug ist. Die Helligkeit jedes Polygons ergibt sich dann aus der Reflexionsfähigkeit der Oberfläche und der Intensität des Umgebungslichtes: Die Fläche reflektiert einen bestimmten Anteil des Umgebungslichtes. Die Reflexionsfähigkeit ist also ein Faktor, der sinnvollerweise zwischen 0 und 1 liegt. Die Helligkeit der Fläche ist dann:
IFläche=Fref* I Umgebungslicht
Dabei ist Fref die Reflexionsfähigkeit. Für Farbbilder muß diese Formel für jede der Grundfarben Rot, Grün und Blau einzeln mit jeweils einem eigenen Faktor berechnet werden, als Ergebnis erhalten Sie dann die Intensitäten der drei Farbkomponenten, die zusammen (gemischt) die Farbe der Fläche ergeben.
Jetzt gehen wir einen Schritt weiter: Wir führen Punktlichtquellen ein, die ein Objekt, also die Flächen, aus denen es besteht, direkt beleuchten können. In diesem Fall gibt es zwei Arten von Reflexion: Diffuse und direkte Reflexion. Ein perfekter diffuser Reflektor strahlt aus einer Richtung ankommendes Licht nach allen Richtungen gleichmäßig ab. Die Stärke der Reflexion hängt dabei vom Einfallswinkel des Lichtstrahles ab. Das Gesetz der geometrischen Optik, das dafür zuständig ist, heißt Lambert’s Cosinus-Gesetz (siehe Bild 2). Wenn die Oberfläche kein perfekter diffuser Reflektor ist, gibt es wieder einen Faktor zwischen 0 und 1, der die Reflexionseigenschaften angibt. Auch hierbei kann, je nach Material, ein unterschiedlicher Faktor für jede der Grundfarben vorhanden sein.
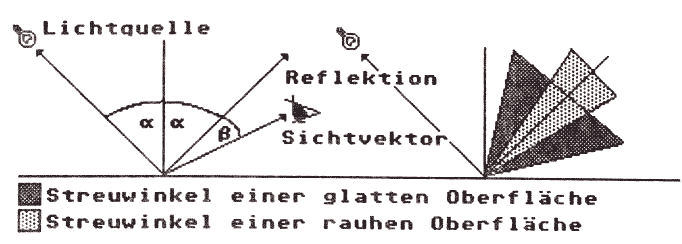 Bild 3 & 4: "Echte" Oberflächen reflektieren nicht nur diffus, sondern auch direkt nach dem Gesetz "Einfallswinkel gleich Ausfallswinkel". Dies gilt aber nur für den idealen Fall, reale Oberflächen streuen das einfallende Licht um einen bestimmten Winkel. Je größer der Streuwinkel, desto matter erscheint die Oberfläche. Kleine Streuwinkel in Verbindung mit einem großen Reflektionsfaktor für die direkte Reflektion ergeben deutliche Schlaglicht-Effekte. Der Anteil des direkt reflektierten Lichtes berechnet sich folgendermaßen:
Bild 3 & 4: "Echte" Oberflächen reflektieren nicht nur diffus, sondern auch direkt nach dem Gesetz "Einfallswinkel gleich Ausfallswinkel". Dies gilt aber nur für den idealen Fall, reale Oberflächen streuen das einfallende Licht um einen bestimmten Winkel. Je größer der Streuwinkel, desto matter erscheint die Oberfläche. Kleine Streuwinkel in Verbindung mit einem großen Reflektionsfaktor für die direkte Reflektion ergeben deutliche Schlaglicht-Effekte. Der Anteil des direkt reflektierten Lichtes berechnet sich folgendermaßen:
Idirekt=ILicht * Fdirekt * cos(β)
Dabei ist F ein Faktor, der die direkte Reflektionsfähigkeit der Fläche angibt. Beachten Sie, daß das Ergebnis nicht nur vom Einfallswinkel des Lichtes, sondern vom Winkeides Reflektions- zum Sichtvektor abhängt.
Jetzt existieren zwei Lichtquellen: Das Umgebungslicht und das Licht, das von der Punktlichtquelle kommt. E> ist einsichtig, das sich die Intensiven dieser Lichtquellen addieren. Das einfache Beleuchtungsmodell für diffus reflektierende Flächen lautet somit:
I<sub>fläche</sub> = F<sub>U</sub>*I<sub>U</sub> + F<sub>Diff</sub>/COS(α)*I<sub>Diff</sub>
Dabei ist Fdiff der diffuse Reflexionsfaktor der Fläche, cos(α) der Einfallswinkel des Lichtes und I die Intensität Punktlichtquelle (FU und IU sind der Reflexionsfaktor und die Intensität für das Umgebungslicht).
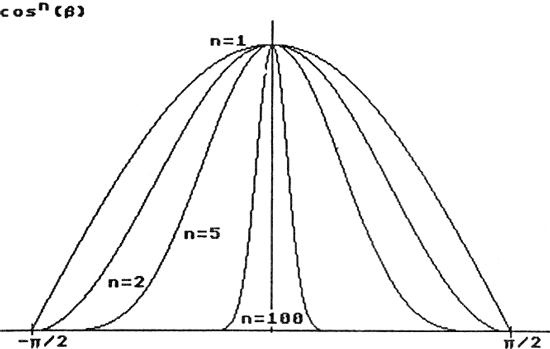 Bild 5: Im Beleuchtungsmodell für die direkte Reflektion wird der Streuwinkel durch die Potenz des Cosinus des Winkels zwischen Reflektions- und Sichtvektor bestimmt. Große Werte für n ergeben kleine Streuwinkel, was zusammen mit großen Reflektionsfaktoren deutliche Schlaglichter ergibt, während kleine Reflektionsfaktoren matte, papierartig scheinende Oberflächen erzeugen. Wählt man unterschiedliche Faktoren für die drei Grundfarben, kann man gefärbte Schlaglichter, wie sie z.B. bei Metallen auftreten, erzeugen.
Bild 5: Im Beleuchtungsmodell für die direkte Reflektion wird der Streuwinkel durch die Potenz des Cosinus des Winkels zwischen Reflektions- und Sichtvektor bestimmt. Große Werte für n ergeben kleine Streuwinkel, was zusammen mit großen Reflektionsfaktoren deutliche Schlaglichter ergibt, während kleine Reflektionsfaktoren matte, papierartig scheinende Oberflächen erzeugen. Wählt man unterschiedliche Faktoren für die drei Grundfarben, kann man gefärbte Schlaglichter, wie sie z.B. bei Metallen auftreten, erzeugen.
Natürlich ist es möglich, daß eine Fläche von mehreren Punktlichtquellen beleuchtet wird. In diesem Fall addieren sich auch diese Intensitäten:
|
Ifläche = FU * IU +
|
|
(FDiff*COS(α)*I)i
|
Natürlich hat dann jede Lichtquelle einen eigenen Einfallswinkel und eine eigene Intensität, während der Reflexionsfaktor für alle Lichtquellen gleich ist, denn dieser ist ja eine Eigenschaft des beleuchteten Materials, nicht der Lichtquelle.
Jetzt tun wir so, als sei die Entfernung einer Lichtquelle völlig gleichgültig. Das es nicht so ist, ist wohl jedem unmittelbar einsichtig; eine Taschenlampe aus 300 Metern Entfernung kann man kaum sehen, wenn sie nahe genug ist, blendet sie. Also bauen wir noch einen Entfemungsfaktor ein. An sich, physikalisch betrachtet, ändert sich die bei einem Betrachter ankommende Lichtenergie nicht linear mit der Entfernung, sondern mit dem Quadrat der Entfernung. Es zeigt sich allerdings im Experiment, daß dies bei Computerbildern zu unnatürlich wirkenden Intensitätssprüngen führt, da die Objekte meist relativ nah am Betrachterstandpunkt liegen. Also verzichtet man auf die Physik und verwendet statt dem korrektem Faktor 1/d2 (d ist der Abstand der Lichtquelle) einfach 1/d. Das Beleuchtungsmodell sieht dann so aus:
|
Ifläche = FU * IU +
|
|
(FDiff*COS(α)*I/d),
|
Das ist alles noch ganz einfach. Leider hat praktisch jedes Material, selbst mattes Papier, die Eigenschaft, auch Licht in eine bestimmte Richtung, also direkt zu reflektieren. Das funktioniert im Prinzip nach dem bekannten optischen Gesetz ‘Einfallswinkel gleich Ausfallswinkel, das Licht wird also im gleichen Winkel und auf der gleichen Ebene wieder reflektiert, in dem es auf die reflektierende Fläche einfällt (siehe Bild 3). Leider wird das Licht dabei aber auch leicht gestreut, man sieht diese direkten Reflexionen also nicht nur dann, wenn man direkt auf den Vektor des reflektierten Lichtes schaut, sondern auch aus Winkeln, die etwas abseits liegen. Glatte (glänzende) Oberflächen haben schmale Streuwinkel, matte Oberflächen weitere (Bild 4). Daraus ergibt sich natürlich auch, daß Schlaglichter mit verändertem Betrachterstandpunkt mitwandern.
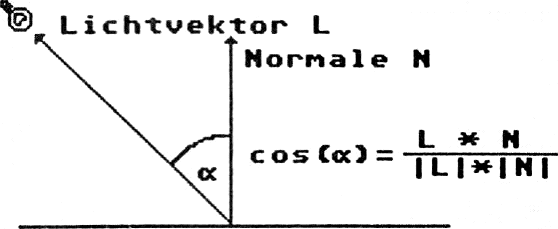 Bild 6: Der Cosinus des Winkels zwischen L und N läßt sich leicht mit Hilfe des Skalarproduktes berechnen: L=Pl - Pp, mit PI=Position der Lichtquelle und Pp=Position des zu berechnenden Pixels. Das Skalarprodukt ist definiert als a * b = lal * \b\ * cos(a), wobei a = Winkel zw. a und b. Außerdem läßt sich das Skalarprodukt in Komponentenform schreiben als:
Bild 6: Der Cosinus des Winkels zwischen L und N läßt sich leicht mit Hilfe des Skalarproduktes berechnen: L=Pl - Pp, mit PI=Position der Lichtquelle und Pp=Position des zu berechnenden Pixels. Das Skalarprodukt ist definiert als a * b = lal * \b\ * cos(a), wobei a = Winkel zw. a und b. Außerdem läßt sich das Skalarprodukt in Komponentenform schreiben als:
cos( a)= xaxb+vavb+za*zb
'■ixa'+yaJ+zaJ * \xbJ+yb~+zbJ Die Länge von L (der Wert d im Beleuchtungsmodell) ist einfach:
d=\IJ = yxIT+fU+zV
Jeder von Ihnen kennt diesen direkten Reflexionseffekt, die sogenannten Schlaglichter. Auf den meisten Materialien haben Schlaglichter leider selten die Farbe der reflektierenden Oberfläche, sondern die Farbe des einfallenden Lichtes (Ein Schlaglicht auf blauem Lack, der mit weißem Licht beleuchtet wird, ist weiß, nicht blau). Eine Ausnahme machen nur die meisten Metalle, die auch die Farbe des Schlaglichtes verändern. Im allgemeinen verzichtet man darauf, die tatsächlichen physikalischen Verhältnisse zu simulieren, sondern verwendet empirische, einfache Modelle - statt einer Funktion, die den Zusammenhang von Wellenlänge, Einfallswinkel und Intensität des reflektierten Lichtes angibt, einfach eine Konstante für die Schlaglicht-Reflexionsfähigkeit. Wenn Sie diese Konstante für jede der drei Grundfarben unabhängig wählen, erhalten Sie gefärbte Schlaglichter auch bei weißem Licht, was natürlich nicht die gleichen Ergebnisse liefert, wie eine Funktion, die die Reflexionsfähigkeit aus Wellenlänge und Einfallswinkel des Lichtes berechnet.
Das Beleuchtungsmodell mit Schlaglichtern sieht dann so aus:
|
Ifläche = FU * IU +
|
|
((I/d)* (FDiff*COS(α)+ Fspec*COSn(β)))i
|
Dabei ist ß der Winkel zwischen dem reflektierten Licht und dem Sichtvektor, während die Potenz n des Cosinus die Stärke der Streuung des Lichtes (siehe Bild 5) angibt. Kleine Werte für n ergeben weite Streuung, also matte Oberflächen wie Papier, große Werte ergeben enge Streuungen, wie von polierten Flächen. Fspec ist der Faktor, der angibt, welcher Teil der Intensität der Lichtquelle I als Schlaglicht reflektiert wird. I, d, α, β und n müssen natürlich für jede Lichtquelle getrennt angegeben werden, während die beiden Faktoren, wie oben, Oberflächeneigenschaften sind.
Dies ist ein recht primitives Beleuchtungsmodell, da es kaum Eigenschaften realistischer Lichtquellen berücksichtigt und auch die tatsächlichen physikalischen Gegebenheiten nur sehr unvollkommen simuliert. Eine echte Lichtquelle beispielsweise strahlt nicht wie die verwendeten Punktstrahler in alle Richtungen, außerdem ist eine normale Lampe alles andere als punktförmig. Flächige Lichtquellen und alle möglichen Spezialeffekte sind aber doch etwas zu kompliziert, um sie hier zu verwenden.
 Bild 7a & b: Flatshading und Gouraudshading im Vergleich. Bilder von Hartmut Wagener, berechnet auf einem ST mit einer Grafikkarte von Omega Datentechnik.
Bild 7a & b: Flatshading und Gouraudshading im Vergleich. Bilder von Hartmut Wagener, berechnet auf einem ST mit einer Grafikkarte von Omega Datentechnik.
Weitere Effekte, die man einbauen kann, beschäftigen sich mit der Eigenschaft realer Objektive, nur einen begrenzten Bildausschnitt scharf abzubilden, der sogenannten Tiefenschärfe. Auch so etwas kann man simulieren.
Schließlich gibt es noch, je nach verwendeter Bildgenerierungstechnik, verschiedene Methoden, Schatten und Transparenz darzustellen. Darauf kommen wir später zurück.
Anwendung von Beleuchtungsmodellen
Wir wissen jetzt zwar, wie man das Verhalten des Lichtes auf Oberflächen in einfacher Näherung berechnen kann, aber wie bringt man eine Oberfläche dazu, entsprechend beleuchtet zu erscheinen ?
Die allereinfachste Methode ist es, einfach jedes Polygon komplett mit gleicher Intensität zu füllen. Denn die Winkel, die im Beleuchtungsmodell angegeben werden, sind auf die Oberflächennormale bezogen. Und von allen Pixeln, die innerhalb des Polygons liegen, gibt es nur eine Normale - nämlich die der ganzen Fläche. Also wendet man das Beleuchtungsmodell für jedes Polygon einmal an und füllt dann das ganze Polygon mit der dabei berechneten Farbe. Allerdings fällt dabei dem aufmerksamen Beobachter sofort auf, daß Schlaglichter nicht besonders sinnvoll sind, wenn man ganze Polygone mit der gleichen Intensität ausfüllt. Schließlich ist ein Schlaglicht örtlich begrenzt, so daß Bilder etwas merkwürdig aussähen, wenn größere Flächen mit der Intensität eines Schlaglichtes ausgefüllt würden. Man kann sich in diesem Fall also mit dem einfachen Beleuchtungsmodell mit diffuser Reflexion behelfen. Was man braucht, ist nur das einfache Beleuchtungsmodell und die Oberflächennormale des Polygons. Mit Hilfe der Positionen der Lichtquellen kann man dann leicht den Cosinus des Winkels zur Oberflächennormale berechnen, sowie die Entfernung der Lichtquelle vom Polygon (Bild 6). Schon hat man einfache 3D-Bilder, mit relativ wenig Rechenaufwand.
Weichschattierung
Nur leider sehen diese Bilder nicht besonders realistisch aus. Welches Gesicht (nur als Beispiel) ist schon aus Polygonen zusammengesetzt? Irgendwie muß man also versuchen, ein Bild so aussehen zu lassen, als sei es nicht aus Polygonen zusammengesetzt, sondern aus weich und sanft gerundeten Formen...
Das Beleuchtungsmodell ergibt, da pro Polygon nur eine Oberflächennormale vorhanden ist, für das ganze Polygon das gleiche Ergebnis. Nun liegt aber selten ein Polygon so ganz allein in der Gegend herum. Im allgemeinen liegen noch ein paar andere Polygone drumherum, jedes mit seinereigenen Normale. Was wollen uns diese Worte sagen ? Nun, wenn wir eine Normale haben und ein paar umliegende Normalen, dann kann man ja die Intensitätswerte zwischen den Polygonmitten interpolieren und so einen kontinuierlichen Intensitätsverlauf erreichen. Diese Idee hatte ein Herr Gouraud bereits 1971. Ein Ergebnis des Verfahrens sehen Sie in Bild 7. im Vergleich mit dem flach-schattierten Bild.
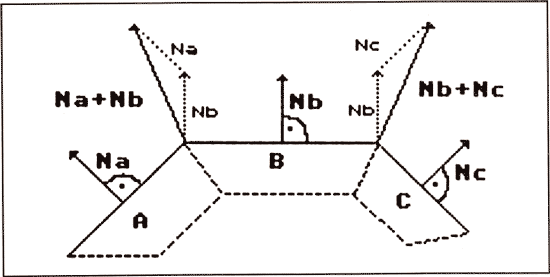 Bild 8: Die Normalen an den Ecken von zwei Polygonen ergeben sich aus der Summe der Normalen der Flächen, die an dem Punkt Zusammentreffen. Da die Länge der Normalen für unsere Anwendung unerheblich ist, kann auf eine Normierung verzichtet werden.
Bild 8: Die Normalen an den Ecken von zwei Polygonen ergeben sich aus der Summe der Normalen der Flächen, die an dem Punkt Zusammentreffen. Da die Länge der Normalen für unsere Anwendung unerheblich ist, kann auf eine Normierung verzichtet werden.
Wie funktioniert’s?
Am einfachsten ist es, wenn wir davon ausgehen, daß alle unsere Polygone Dreiecke sind. Wenn nicht, ändert sich nichts am Prinzip, man muß nur schrecklich viele Dinge zusätzlich beachten. Bleiben wir also bei einem Dreieck. Außerdem sollten wir davon ausgehen, daß wir uns bereits im Bildschirmkoordinatensystem befinden, am einfachsten ist eine solche Shading-Routine innerhalb des Hidden Surface-Algorithmus zu implementieren. Sehr einfach ist das beispielsweise mit dem z-Buffer. Was wir brauchen, sind erst einmal Intensitäten für jede Seite des Dreiecks. Wir kennen die Normale der Fläche. Außerdem liegen um das Dreieck noch andere Flächen herum, die ebenfalls eine Flächennormale liabSn. In Bild 8 sehen Sie, was wir tun: Wir berechnen für jeden Eckpunkt, an dem sich zwei oder mehr Dreiecke berühren, eine Mittelwert-Normale, die wir im folgenden als die Normale des jeweiligen Eckpunktes bezeichnen wollen. Da die Länge der Normalen hier überhaupt nicht interessiert, nur die Richtung ist wichtig (im Beleuchtungsmodell wird ja nur der Winkel eines Lichtstrahls zur Normalen verwendet), können wir den Mittelwert der Normalen durch einfaches Addieren der Flächennormalen erhalten.
Jetzt hat jeder Eckpunkt unseres Dreiecks eine Normale. Mit Hilfe dieser Normalen, die sich aus den umgebenden Dreiecken mitergeben, können wir für jeden der Eckpunkte eine eigene Intensität mit Hilfe des Beleuchtungsmodells berechnen. Wie berechnet man jetzt aber die Intensitäten der übrigen Pixel, die innerhalb des Dreiecks liegen?
Sehen Sie sich Bild 9 an. Stellen Sie sich vor, Sie tasten das Bild von oben nach unten (oder umgekehrt, wie Sie wollen) zeilenweise ab. Dabei stellen Sie zuerst einmal fest, welche Seiten des Dreiecks sich unter der gedachten Abtastzeile befinden. Bei einem Dreieck ist das sehr einfach, viele Möglichkeiten gibt es ja auch nicht.
Es ist nun sehr einfach, für jede Seite, die von der Abtastzeile geschnitten wird, die Intensitäten zu interpolieren. Ein Beispiel: Der Punkt A habe die Bildschirmkoordinaten Y=240, für Punkt B sei Y=120, für Punkt C Y=100. Die Abtastzeile schneidet die Seiten AB und AC bei Punkt N mit dem Y-Wert Yn= 180. Wir kennen die Intensitäten bei A, B und C. Für die Seite AB ergibt sich also ein Intensitätsunterschied dI = Ia-Ib. Insgesamt überstreicht die Abtastzeile die Seite AB mit
Ya-Yb = 240 - 120 = 120 Schritten,
ein Schritt entspricht also einem Intensitätsunterschied von
I abfaktor = -dI /(Ya-Yb)
Die Abtastzeile befindet sich bei Yn=180, also ist sie Ya - Yn = 60 Schritte in y-Richtung von A entfernt.
Daraus ergibt sich eine Intensität für Punkt N von
In = 60 * I abfaktor
oder, allgemein für jeden Punkt der Strecke AB:
In = (Ya - Y abtastzeile) * I abfaktor
Genauso funktioniert das mit den Pixeln auf der Strecke AC oder jeder anderen gerade aktiven Strecke des Dreiecks; lediglich der Faktor und der Bezugspunkt ändern sich.
Wenn die beiden Intensitäten für die Punkte N und M bekannt sind, kann man das gleiche Verfahren für die Berechnung der Intensitäten aller Pixel auf der Abtastzeile zwischen N und M verwenden. Zuerst einmal berechnet man die Intensitätsdifferenz
dInm = In - Im
Dann muß noch die Anzahl der Schritte zwischen N und M berechnet werden:
Schritte = Xm - Xn
Dabei lassen sich Xm und Xn auf die gleiche Methode errechnen, wie die Intensitätsveränderung zwischen A und B bzw. A und C, fehlerfreiere Ergebnisse erhält man jedoch, wenn man dazu einen Algorithmus zum Linienzeichnen verwendet. Das liegt daran, daß die Auflösung des Bildschirms es ja im allgemeinen nicht erlaubt, eine diagonale Linie so zu zeichnen, wie sie in Wirklichkeit auszusehen hat. Die Computertypischen Treppchen sind die Folge. Berechnet man einfach X- und Y- Koordinaten nach einer Geradengleichung, werden meist Nachkommastellen entstehen, die man nicht einfach runden kann, ohne grobe Bildfehler in Kauf zu nehmen. Solche Fehler lassen sich mit einem Linienzeichen-Algorithmus vermeiden. Das Betriebssystem verwendet auch derartige Verfahren, wenn eine Linie zu zeichnen ist, aber leider zeichnet das Betriebssystem immer mit der gleichen Intensität. Gouraud-Shading oder Anti-Aliasing (Verfahren zur Beseitigung der Computer-Treppchen) mit 16 Farben ist aber zugegebenermaßen auch nicht sehr sinnvoll. Die Intensitätsveränderung zwischen zwei Pixeln zwischen N und M ist dann:
dI = -dInm / (Xm - Xn).
Diesen Wert muß man nur einmal berechnen, dann kann man die Routine für die restlichen Pixel zwischen N und M so formulieren:
For i = N to M DO
I(Pixel I+1) = I(Pixelj) + dl;
So einfach ist das. Im Grunde tut man hier nichts anderes, als zwei Geradengleichungen zu lösen, deren Parameter x (zwischen N und M) bzw. y (zwischen den Eckpunkten) und deren Funktionswert eine Intensität ist. Da es sich um Geradengleichungen handelt, ist es nicht erforderlich, jeden Wert neu zu berechnen, es genügt, einen einmal berechneten Wert zu dem Wert des vorherigen Pixels zu addieren. Das geht natürlich nur, weil wir uns bereits im Bildschirmkoordinatensystem befinden, das ja ausschließlich aus Integer-Koordinaten besteht. Um ein ganzes Bild auf diese Weise zu schattieren, muß man jedes einzelne Dreieck oder Polygon, aus dem das Bild besteht, durch den Algorithmus schicken. Um gleich mehrere Fliegen mit einer Klappe zu schlagen, kann man natürlich zusätzlich zur Intensitäts-Berechnung gleich die z-Koordinate jedes Pixels mitberechnen (Ist auch wieder nur eine einfache Geradengleichung - funktioniert also ganz genauso) und in einem Buffer für jedes Pixel der Zeile speichern. Dann hat man einen Spezialfall des z-Buffer-Algorithmus (siehe April-Heft) implementiert, der sich Scanline-z-Buffer-Algorithmus nennt (Scanline=Abtastzeile).
 Bild 9: Bei der Weichschattierung nach Gouraud werden zuerst die Intensitäten an den Eckpunkten des Polygons berechnet. Dann wird linear entlang der Linie ab bzw. ac interpoliert, um den Intensitätsverlauf entlang der Seiten AB und AC zu erhalten. Damit sind die Intensitäten bei N und M bekannt. Auf die gleiche Weise kann jetzt zwischen N und M interpoliert werden, um so die Intensität jedes Pixels zwischen N und M zu erhalten. Die Lage der Punkte N und M wird von der Abtastzeile bestimmt. Ob man die Polygone von rechts nach links, von oben nach unten, oder wie auch immer abtastet, ist dabei völlig gleichgültig, lediglich die Methode der Interpolationsrechnung muß angepaßt werden. Die Normalen bei A, B und C, aus denen sich im obigen Beispiel direkt die eingezeichneten Intensitäten ergeben, haben einen extrem großen Einfluß auf das Aussehen der Schattierung. Dies ist ein großer Nachteil des Verfahrens, da die Normalen der Eckpunkte sehr stark von Form und Größe des Polygons selbst, aber auch der umliegenden Polygone abhängen. Die einfache lineare Interpolation der Intensitäten führt daher manchmal zu unnatürlichen Schattierungen.
Bild 9: Bei der Weichschattierung nach Gouraud werden zuerst die Intensitäten an den Eckpunkten des Polygons berechnet. Dann wird linear entlang der Linie ab bzw. ac interpoliert, um den Intensitätsverlauf entlang der Seiten AB und AC zu erhalten. Damit sind die Intensitäten bei N und M bekannt. Auf die gleiche Weise kann jetzt zwischen N und M interpoliert werden, um so die Intensität jedes Pixels zwischen N und M zu erhalten. Die Lage der Punkte N und M wird von der Abtastzeile bestimmt. Ob man die Polygone von rechts nach links, von oben nach unten, oder wie auch immer abtastet, ist dabei völlig gleichgültig, lediglich die Methode der Interpolationsrechnung muß angepaßt werden. Die Normalen bei A, B und C, aus denen sich im obigen Beispiel direkt die eingezeichneten Intensitäten ergeben, haben einen extrem großen Einfluß auf das Aussehen der Schattierung. Dies ist ein großer Nachteil des Verfahrens, da die Normalen der Eckpunkte sehr stark von Form und Größe des Polygons selbst, aber auch der umliegenden Polygone abhängen. Die einfache lineare Interpolation der Intensitäten führt daher manchmal zu unnatürlichen Schattierungen.
Man vergleicht dann vor der Berechnung der Intensität die z-Koordinate im Buffer mit der gerade für das aktuelle Polygon berechneten. Ist der Wert im Buffer kleiner, braucht man gar nicht weiterzumachen, denn dann ist dieses Pixel bereits von einem näher beim Betrachter liegenden Objekt belegt.
Bevor wir uns einem etwas raffinierteren Verfahren zuwenden, sollen noch ein paar Probleme des Gouraud-Shading vorgeführt werden:
-
Gouraud-Shading ergibt im allgemeinen dann die besten Resultate, wenn man ein einfaches Beleuchtungsmodell ohne Schlaglichter verwendet. Der Grund dafür ist, daß die Intensitätsverteilung extrem von der Form und Lage der Polygone, aus denen das Objekt besteht, abhängt. Es gibt allerdings Ausnahmefälle.
-
Einfaches Gouraud-Shading ergibt starke Shading-Wechsel, die sehr unnatürlich wirken, wenn man es in Animationssequenzen verwendet. Es gibt allerdings Verbesserungen, die diesen Fehler korrigieren.
-
Bild 10 zeigt einen gezackten Oberflächen-Verlauf, der nach Gouraud-Schattierung flach aussehen würde. Das Problem läßt sich durch Einfügen zusätzlicher Polygone lösen.
-
Es entstehen sogenannte Mach-Band-Effekte. Dies sind helle Streifen an der Grenze zwischen zwei Polygonen. Der Grund für diesen Fehler liegt darin, daß zwar die Interpolation der Intensitäten an der Übergangsstelle zwischen zwei Polygonen stetig ist, nicht aber die erste Ableitung der Interpolationsfunktion.
-
Das Verfahren kann natürlich nicht unterscheiden, ob ein deutlicher Lichtwechsel an einer bestimmten Stelle des Objektes eventuell erwünscht ist. Alle Kanten werden durch das Schattieren gerundet, auch wenn sie scharf bleiben sollten. Diesen Effekt kann man beseitigen, indem man an den entsprechenden Stellen die Normalen für die Eckpunkte so zurechtbiegt, daß eine scharfe Schattierungsgrenze entsteht (d.h. man verzichtet an der entsprechenden Stelle auf eine Interpolation der Normalen).
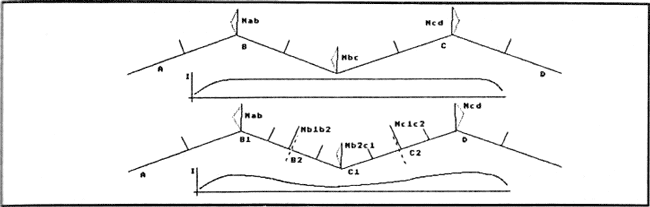 Bild 10: An diesen beiden von der Seite gesehenen Flächenzügen sieht man deutlich eines der Probleme, die beim Gouraud-Verfahren auftreten. Im oberen Bild sind die aus den Flächennormalen gebildeten Ecknormalen Nab, Nbc und Ncd gleich. Die Folge: Das weichschattierte Bild sieht aus, als ei der Flächenabschnitt flach (Siehe obere Intensitätskurve). Man kann dieses Problem durch Aufteilen der Polygone B und C in zwei Teilpolygone lösen; die dadurch zusätzlich entstehenden Normalen Nb1b2 und Nc1c2 sorgen für eine dem Flächenverlauf entsprechende Intensitätskurve.
Bild 10: An diesen beiden von der Seite gesehenen Flächenzügen sieht man deutlich eines der Probleme, die beim Gouraud-Verfahren auftreten. Im oberen Bild sind die aus den Flächennormalen gebildeten Ecknormalen Nab, Nbc und Ncd gleich. Die Folge: Das weichschattierte Bild sieht aus, als ei der Flächenabschnitt flach (Siehe obere Intensitätskurve). Man kann dieses Problem durch Aufteilen der Polygone B und C in zwei Teilpolygone lösen; die dadurch zusätzlich entstehenden Normalen Nb1b2 und Nc1c2 sorgen für eine dem Flächenverlauf entsprechende Intensitätskurve.
Phong-Shading
Eine verbesserte Form des Gouraud-Shading ist das Phong-Shading, benannt nach seinem Erfinder Bui-Tuong Phong. Im Prinzip funktioniert das genau wie Gouraud-Shading, allerdings werden nicht die Intensitäten entlang der Abtastzeile interpoliert, sondern die Normalen. Dadurch wird das Verfahren erheblich rechenintensiver, denn zum einen müssen die Normalen interpoliert werden, was schon an sich aufwendiger ist, zum anderen muß aber auch das Beleuchtungsmodell jetzt für jedes Pixel einzeln angewandt werden, da ja nicht mehr einmal berechnete Intensitäten interpoliert werden. Der Algorithmus selbst ist auch nicht schwieriger als der des Gouraud-Shading (schließlich ist er von diesem kaum verschieden), weshalb er hier auch nicht näher besprochen werden soll. Phong-Shading läßt sich aber auch sehr gut mit einem Beleuchtungsmodell mit Schlaglichtern verwenden, die Ergebnisse sind meist weit realistischer als bei Gouraud-Shading. Einige der oben angeführten Probleme (z.B. das Animationsproblem) zeigt aber auch dieses Verfahren in seiner einfachen Form.
Oberflächenstrukturen
Inzwischen sind wir soweit, daß wir Oberflächen mit weichen, ‘natürlichen' Farbverläufen darstellen können. Leider sind die wenigsten Oberflächen glatt, genauso selten wie Oberflächen einfarbig sind.
Wirklich rauhe Oberflächen, die strukturiert sind, wie Apfelsinenschalen, Stoffe oder Holz, kann man nicht einfach im Beleuchtungsmodell durch den Parameter für die direkte Reflexionsfähigkeit erzeugen. Eine solche deutliche Struktur muß durch einen Trick erreicht werden. Dazu variiert man über eine komplizierte Funktion den Normalenvektor einer Oberfläche. Dies kann entweder eine zufällige Variation sein oder eine Funktion, die sich an mathematischen Modellen orientiert. Auch Bilder von Mustern können als Grundlage für die Störfunktion verwendet werden. Besonders einfach ist dieses Verfahren mit Phong-Shading zu implementieren - schließlich verlangt dieses Verfahren sowieso die Berechnung einer Normalen für jedes Pixel. Die Normalen müssen dann nur noch mit der Störungsfunktion ein wenig ‘verbogen’ werden.
Viele Oberflächen sind irgendwie gemustert oder vielfarbig oder beschrieben usw., bekanntes Beispiel: die Coca-Cola-Dose. Einen Zylinder zu definieren, der wie Blech aussieht, ist mit Phong-Shading kein Problem. Jetzt müßte man diesen Zylinder nur noch mit dem Cola-Label bekleben. So etwas erreicht man mit einer sogenannten Mapping-Funktion. Dazu braucht man erst einmal ein zweidimensionales Bild der gewünschten Oberfläche. Dann definiert man eine Funktion, die jedes Pixel des zweidimensionalen Bildes einem Punkt des 3D-Objektes zuordnet. Das ist glücklicherweise nicht schwierig. Den ganzen Vorgang nennt man ‘Texture-Mapping’.
Wenn Sie ein 2D-Bild mit einer rauhen Oberfläche (siehe oben) verwenden und dieses Bild auf ein 3D-Objekt mappen, dann sieht das so aus, als ob Sie ein Photo einer rauhen Oberfläche auf eine glatte Oberfläche geklebt hätten. Deswegen muß man wirklich rauh aussehende Oberflächen auch mit dem viel rechenintensiveren Verfahren der Normalenvektor-Störung erzeugen.
Diese Methoden sind sehr geeignet, wirklich gut und realistisch aussehende Oberflächen zu erzeugen. Selbst mit einfachen Schattierungsmethoden sehen Bilder sehr gut aus, wenn sie eine Oberflächenstruktur und ein Oberflächenmuster erhalten.
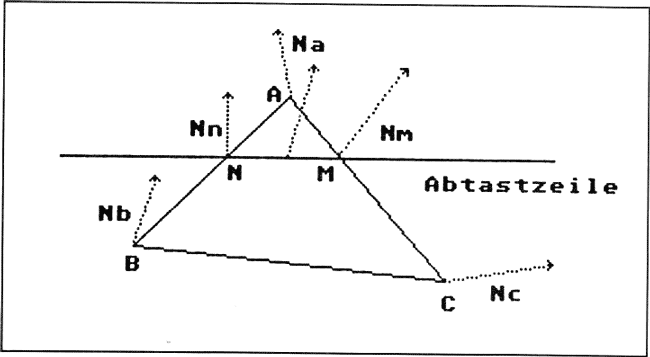 Bild 11: Phong-Shading. Bei diesem Verfahren werden nicht die Intensitäten bei A, B und C aus den Normalen Na, Nb und Nc berechnet, sondern es werden aus diesen Normalen die Normalen bei N und M interpoliert, aus diesen dann wiederum die Normalen jedes Pixels zwischen N und M. Die Intensität für jedes Pixel wird dann mit Hilfe dieser Normalen mit dem Beleuchtungsmodell berechnet. Damit ist natürlich erheblich mehr Rechenaufwand verbunden. Dafür sind die Ergebnisse meist erheblich realistischer, überhaupt ist es erst mit Phong-Shading sinnvoll, kompliziertere Beleuchtungsmodelle (mit Schlaglichtern usw.) zu verwenden.
Bild 11: Phong-Shading. Bei diesem Verfahren werden nicht die Intensitäten bei A, B und C aus den Normalen Na, Nb und Nc berechnet, sondern es werden aus diesen Normalen die Normalen bei N und M interpoliert, aus diesen dann wiederum die Normalen jedes Pixels zwischen N und M. Die Intensität für jedes Pixel wird dann mit Hilfe dieser Normalen mit dem Beleuchtungsmodell berechnet. Damit ist natürlich erheblich mehr Rechenaufwand verbunden. Dafür sind die Ergebnisse meist erheblich realistischer, überhaupt ist es erst mit Phong-Shading sinnvoll, kompliziertere Beleuchtungsmodelle (mit Schlaglichtern usw.) zu verwenden.
Schatten und Transparenz
das ist der letzte Schritt in Sachen Realismus. Leider ist es nicht ganz einfach und auch keineswegs effizient, solche Effekte mit ‘traditionellen’ Schattierungsverfahren zu erreichen. Deswegen werden wir in der nächsten Folge ein Verfahren kennenlernen, das so ziemlich alle Effekte, die heute in der Computergrafik möglich sind, auf einmal und ziemlich elegant erzeugen kann. Leider ist dieses Verfahren, das den schönen Namen ‘Ray Tracing’ trägt, auch furchtbar rechenintensiv. Dennoch, ‘Ray Tracing’ ist eine der interessantesten Techniken zur Erzeugung von Computerbildern. Bis zum nächsten Mal also.
CS