Jeder kennt den Gemüsegarten des Informatikers. In der einen oder anderen Form sind uns die verschiedenen Sorten des „Lieblingsgemüses“ Baum schon über den Weg gelaufen. Meistens verursachten sie Kopfschmerzen der Art „wie war das noch gleich, wie ging das? nein nein, so war das nicht...“. Hier möchte ich Sie mit der neuesten, vielleicht besseren Züchtung bekanntmachen: den sogenannten „Skip Lists“.
Keine Angst. Nicht allzu viel Theorie, jedoch einen einfachen Algorithmus werde ich vorstellen, der zudem noch universell einsetzbar ist. Ein paar Sätze über die Flora muß ich jedoch vorausschicken.
Bäume
... sind im Informatikergarten auf den Kopf gestellt. Die Wurzel hängt in der Luft, und die Äste und Blätter baumeln normalerweise nach unten. Einen regelrechten Stamm gibt es nicht. (Viel treffender wäre es, wenn man Bäume besser als Wurzelwerk bezeichnen würde, aber wir übernehmen ja alles aus dem Englischen.) Man unterscheidet häufig zwischen Bäumen und Graphen (letztere interessieren uns im folgenden nicht), wobei die Bäume eigentlich eine Spezialisierung des Gewächses Graph sind. In Bäumen steckt schon ein wenig mehr Semantik. Man assoziiert mit ihnen ein gewisses Aussehen und diverse Behandlungsmethoden. Doch dazu später mehr.
Die Stammsorte der Bäume besitzt 2 Äste (Bild 1b), von denen wir den einen „der Ordnung halber“ als seinen linken und den anderen als seinen rechten Sohn (schon wieder diese unzutreffenden Benennungen) bezeichnen.
Eine andere Sorte hat mehrere Äste, respektive Söhne oder Nachfahren. Wollen wir also die beiden Typen unterscheiden, spricht man von binären und n-ären Bäumen (Bild lb).
 Bild 1a: Binärer Baum mit 2 Söhnen, Bild 1b: n-ärer Baum mit n Söhnen
Bild 1a: Binärer Baum mit 2 Söhnen, Bild 1b: n-ärer Baum mit n Söhnen
Jede Verzweigung (Knoten) im Baum enthält einen Identifikationswert. Häufig wird er auch Schlüssel (key) genannt. Bei manchen Baumsorten ist dieser Schlüssel Teil der Information, die dann in jedem Knoten gespeichert wird. Teilweise besteht die Information nur aus diesem Schlüssel. Andere Sorten enthalten nur in den Blättern (Endknoten, Knoten, die keine Söhne mehr haben) Informationen. Aber alle Sorten besitzen in jedem Knoten Schlüssel.
Über diese Informationen ist durch die Baumstruktur eine Ordnung definiert, und man legt im allgemeinen fest, daß alle Informationen in dem linken Sohn und all dessen Söhne kleiner als die Information des Knotens sind. Die der rechten Seite (alle weiter „rechts“ liegenden Geschwister) sind alle größer. Das Wort „kleiner“ hat es so in sich. Was bedeutet es, daß eine Information „kleiner“ als eine andere ist? Bei Zeichenketten bedeutet es wohl, daß eine Zeichenkette lexikalisch kleiner als eine andere ist. Bei Zahlen bedeutet es offensichtlich mathematisch kleiner, also „links“ auf dem Zahlenstrahl.
Kennt man die Definition von „kleiner“, kann man in einem Baum sehr schnell nach Informationen suchen, indem man den Schlüssel der zu suchenden Information mit demjenigen des gerade aktuellen Knotens vergleicht und es abhängig von dem Ergebnis mit einem der Söhne weiterversucht.
Wo wachsen die Bäume?
Häufig werden sie in arrays gepflanzt (Bild 2a). So z.B. die GEM-Resourcen von Programmen, die mit dem Resource-Construction-Set erstellt wurden. (Anmerkung: Ein Objekt in der Resource ist kleiner als das andere, wenn es sich grafisch gesehen innerhalb des anderen befindet.) Solche Bäume wachsen in einem festen Beet und können somit eine bestimmte Größe, respektive die Anzahl der Verzweigungen nicht überschreiten. Viel schöner, aber auch aufwendiger zu pflegen, sind die dynamischen Bäume (Bild 2b), deren Größe von vornherein nicht feststeht, und die zur Laufzeit aufgebaut werden. Und mit diesen werden wir uns hier näher beschäftigen.
Für mathematisch Interessierte: Der Aufwand zum Suchen einer Information in einem n-ären Baum (ein Baum mit maximal n Söhnen) - und damit ist auch die Unterscheidung, ob es diese Information gibt oder nicht, gemeint - ist 0(log(m)) (Logarithmus zur Basis n. Es befinden sich maximal m Informationen in dem Baum). Zum Vergleich: Lineares Suchen, d.h. alle Informationen der Reihe nach untersuchen, dauert im ungünstigsten Fall, also, wenn alle Informationen zu untersuchen sind (z.B. die Information ist nicht vorhanden), m-Zeiteinheiten. Der Aufwand ist damit O(n). Bei einer großen Anzahl von Informationen macht sich das erheblich bemerkbar.
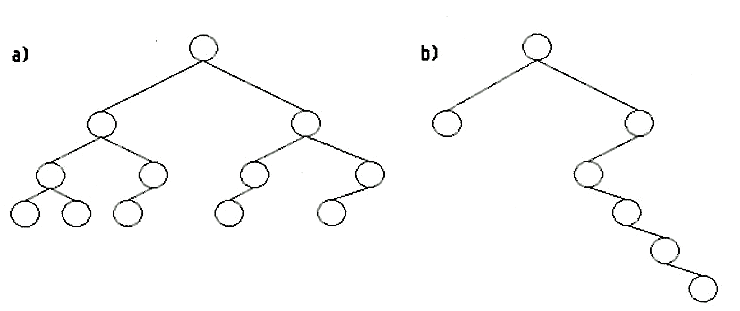 Bild 2a: ausgeglichener binärer Baum, Bild 2b: degenerierter Baum
Bild 2a: ausgeglichener binärer Baum, Bild 2b: degenerierter Baum
Kranke und mißratene Bäume
Aber Bäume sind beim Wachsen und während ihrer Lebenszeit (in der sie manchmal auch gestutzt werden müssen) ständigen Gefahren ausgesetzt. Beide Phasen eines Baumlebens münden in dasselbe Krankheitsbild: degenerierte Bäume. Beim Wachsen eines Baumes bilden sich immer neue Blätter, und es besteht die Möglichkeit, daß immer nur der rechte Ast Söhne bekommt und die anderen Söhne unfruchtbar bleiben. Resultat: der Baum „hängt schief“ (Bild 3b).
Dies wirkt sich fatal für Suchalgorithmen aus. Einige Informationen werden erheblich schneller gefunden als andere. Die durchschnittliche Suchdauer ist größer als bei einem optimal ausbalancierten Baum. Hoppla: optimal ausbalanciert ist ein Begriff, der erst mal erklärt werden muß.
Bildlich gesprochen bedeutet es. daß das Astwerk schön buschig ist, daß, um technischer zu werden, die maximale Astlänge sich von der minimalen Astlänge nur um ein Mindestmaß unterscheidet. Im Normalfall bedeutet dies eine maximale Differenz von einer Astlänge. Die oben erwähnte mathematische Formel ist nur für ausgeglichene Bäume gültig (Bild 3a).
Insofern ist man bestrebt, diesen Fall nicht eintreten zu lassen. Manchmal läßt er sich aber nicht vermeiden. Auch wenn Blätter absterben, kann es passieren, daß davon immer nur ein Ast betroffen ist.
 Bild 3a: Baum als array realisiert, Bild 3b: dynamischer Baum realisiert
Bild 3a: Baum als array realisiert, Bild 3b: dynamischer Baum realisiert
Medizin für Bäume
Die Informatik hat [Adelson, Velskii und Landis sei Dank] Abhilfe durch sogenannte AVL-Bäume geschaffen. Die benötigten Algorithmen garantieren, daß in der Wachstums- und Lebensphase keine Krankheitssymptome auftreten, d.h. die Differenz der Länge der Äste zwischen zwei verschiedenen Söhnen eines jeden Vaterknotens maximal eine Einheit ist. Trifft diese Bedingung auch für den Urvater, die Wurzel des Baumes, zu, spricht man von einem ausgeglichenen Baum.
Die Medizin ist jedoch nicht ohne Nebenwirkungen. Die entsprechenden Algorithmen benötigen Speicherplatz für die Routinen und zur Laufzeit evtl, einen ausreichend großen Stack (wie groß ist das?) wegen des rekursiven Layouts der Funktion (Ok, heutzutage vemachlässigbar und für Besserwisser: Ich weiß auch, es gibt nichtrekursive Verfahren, aber siehe den nächsten Absatz). Weiterhin wird die Laufzeit (dito) oder um im Jargon zu bleiben, die Durchflußgeschwindigkeit der Informationen durch den Baum durch die zusätzlichen Testfunktionen gehemmt.
Und, die Arznei muß sorgfältig hergestellt (programmiert) werden. Letzteres ist häufig der Grund, auf diese Medizin zu verzichten. (Hoffen und Bangen, daß die einzufügenden Informationen in zufälliger Reihenfolge auftreten, da nur dies ein zufriedenstellendes Wachstum ohne Krankheitssymptome ermöglicht.)
Genmanipulation
Da dem nun so ist, versuchte William Pugh [1] einen anderen Ansatz. Und über diesen möchte ich hier berichten. Das Problem läßt sich folgendermaßen charakterisieren:
- Wie läßt sich ein Baum möglichst gleichmäßig aufbauen, ohne daß man die Schlüsselreihenfolge kennt oder gar beeinflussen kann?
- Oder wie lassen sich die Informationen in eine zufällige Reihenfolge bringen, die beim Einsortieren der Informationen einen ausgeglichenen Baum realisieren?
Eine Antwort: Der Aufbau des Baumes muß unabhängig von den Informationen gestaltet werden, also unabhängig von der Ordnung, respektive den Schlüsseln der Informationen. Wie soll das gehen?
In einem Baum bisherigen Typs wird beim Einfügen mit Hilfe des Schlüssels die Stelle gesucht, an der die Information eingefügt werden soll. Und genau diese Stelle müssen wir uns auf andere Weise unabhängig von dem Schlüssel besorgen.
Dabei ist natürlich die Sortierung des Baumes, bestimmt durch unsere „kleiner“-Relation, zu beachten.
Wählen wir einen (nicht ganz passenden) Vergleich aus dem richtigen Leben: Wir suchen eine Telefonnummer in der dicken gelben Schwarte. Man greife also mit der rechten Hand unter das Buch, die Finger der linken Hand liegen auf dem Deckel, und mit dem Daumen hebt man eine „zufällige“ Anzahl Seiten hoch. Wir stellen fest, daß unser Suchbegriff sich entweder im führenden Teil oder im nachfolgenden Teil des Buches befindet. Die Hand greift zwischen die aufgeschlagenen Seiten, und der Vorgang wiederholt sich mit dem Rest des Buches. (Natürlich wird irgendwann sequentiell geblättert.) Probieren Sie’s mal bei diesem Heft mit dem Suchkriterium „Seitenzahl“, ist ja dick genug.
Zentrale Eigenschaft dieses Algorithmus’ ist die Zufälligkeit, mit der wir auf eine bestimmte Seitenzahl stoßen. Wir überspringen dabei eine zufällige Zahl von Blättern.
Pugh wählte eine andere Beschreibungsmethode:
Durch eine aufsteigend sortierte Liste wird sequentiell nach einem Begriff gesucht. Stellen Sie sich eine Straße mit Häusern vor. Die geraden Nummern auf der rechten, die anderen auf der linken Seite. Sie suchen, die Straße entlangradelnd (bei der Hausnummer 1 beginnend) Hausnummer „n“. Dabei werden Sie natürlich nicht den Blick immer pendelnd zwischen den Straßenseiten hin- und herbewegen, sondern immer nur eine Seite (in Deutschland bevorzugt die rechte) mit dem Blick schräg nach vorne betrachten, und im rechten Augenblick, nämlich dann, wenn man kurz vor der entsprechenden Nummer ist, den Kopf der richtigen Seite zuwenden. Dabei werden Hausnummern, die unleserlich oder nicht vorhanden sind, einfach außer acht gelassen. Wir überspringen bei diesem Verfahren mindestens jede 2. Hausnummer.
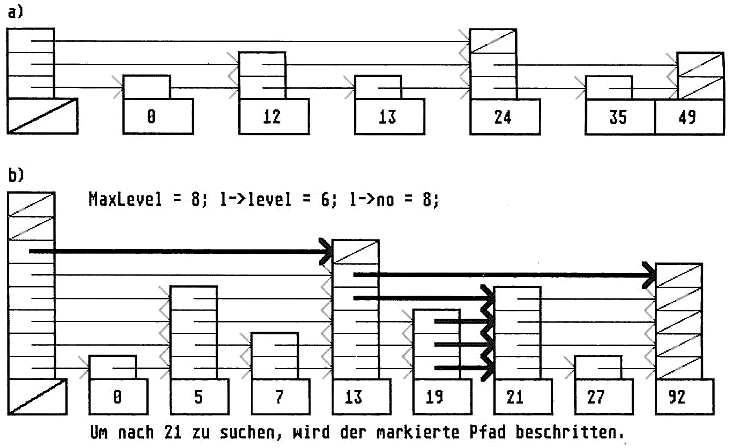 Bild 4a: „skip list“ mit Sprüngen 2l
Bild 4a: „skip list“ mit Sprüngen 2l
Bild 4b: „skip list“ mit willkürlichen Sprüngen
Wie wäre es, wenn wir nicht jede 2. Hausnummer, sondern mehrere auf einmal überspringen (dabei könnten wir schneller fahren), und erst kurz vor dem Ziel langsamer werdend, weniger Hausnummern überspringend, genauer hinschauen würden.
Begriffen? In dem Fall schauen Sie sich jetzt Bild 4a an. Dort ist eine sequentielle Liste mit dargestellt, mit jeweils verschiedener Anzahl von Verweisen auf weiter hinten liegende Elemente. Wenn wir in dieser Liste einen Schlüssel (hier eine Zahl) suchen, folgen wir, von vorne beginnend, zuerst den Pfeilen, die am weitesten nach hinten zeigen (den oberen). Ist der Schlüsselbegriff in der Information, auf die der Pfeil steht, kleiner oder gleich demjenigen, den wir suchen, setzen wir die Suche mit der Gruppe von Pfeilen fort, die PI mal Daumen nur noch halb so weit zeigen. Das setzen wir solange fort, bis wir entweder das Element gefunden haben, oder wir bei Level 0, d.h. der Pfeil zeigt auf das nächste Element in der sortierten Liste, angekommen sind. Alles klar? Das ist das Prinzip.
Was passiert, wenn wir einen neuen Schlüsselbegriff einfügen möchten? Wir müssen uns nicht überlegen, wo wir ihn einsortieren wollen (das legt ja unsere Ordnung „kleiner“ auf dem Schlüsselbegriff fest), sondern ob wir ihn als Sohn oder als Enkel usw. behandeln wollen. Am besten, wir überlassen dies dem Zufall. Und genau das ist die entscheidende Idee:
Instrumente
Wenn wir den Baum aufbauen, überlassen wir es dem Zufall, auf welcher Ebene des Baumes ein neuer Knoten angeordnet wird - also ob er als Sohn, Enkel, Urenkel usw. behandelt wird.
Da der Zufall halt „zufällig“ ist, verteilen sich die Schlüsselbegriffe auch zufällig auf die verschiedenen Ebenen der Nachfahren (Söhne, Enkel ...) unseres Baumes (wie Bild 4b zeigt). Setzen wir einen Zufallszahlengenerator voraus, der gleichverteilte Zahlen eines eingeschränkten Wertebereiches liefert, und ordnen wir jedem Level von Nachfahren eine dieser Zahlen des Wertebereichs fest zu, also z.B. der Wurzel eine 1, den Söhnen eine 3, den Enkeln eine 2 ..., so erfolgt dadurch der Aufbau des Baumes durch Einführung als entsprechender Nachfahre rein zufällig, und damit mit hoher Wahrscheinlichkeit gleichmäßig. Die Zuordnung muß so erfolgen, daß es prinzipiell mehr Enkel als Söhne, als Väter ... gibt. Das ist noch ein Problem!
Alle Ebenen sind damit mit der richtigen Häufigkeit vertreten, (eine genügend große Zahl von Informationen vorausgesetzt.) Um es noch einmal zu sagen: Die Struktur des Baumes ist von der Struktur und Reihenfolge der Information abgekoppelt. Auch das Löschen von Knoten innerhalb des Baumes löscht einen zufälligen Knotentyp (Enkel, Urenkel...), so daß insgesamt die gleichmäßige Struktur des Baumes erhalten bleibt. (Anmerkung: Natürlich lassen sich Arbeitsweisen finden, bei denen sich auch dieser Algorithmus nicht so gut verhält.)
Alles hängt von einem geeigneten Zufallszahlengenerator ab. Der Aufbau des Baumes ist also von der Reihenfolge der Schlüsselbegriffe unabhängig, die somit willkürlich, z.B. auch sortiert sein kann, er hängt von der Reihenfolge der Zufallszahlen ab. (Anmerkung: Gerade sortierte Schlüsselfolgen bereiten konventionellen Algorithmen große Probleme.)
random
Der Zufallszahlenalgorithmus ist nicht beliebig wählbar. Er muß bestimmte Zahlen bevorzugen. Wir wollen, wie oben schon erwähnt, mehr Väter als Söhne haben. Um genauer zu sein: es müssen doppelt soviele Söhne erzeugt werden wie Väter vorhanden sind, um ein optimales Ergebnis zu erzielen. (Verzwickt dabei ist, daß die Anzahl der Väter eigentlich nicht feststeht.) Je besser uns dieses gelingt, desto buschiger gestaltet sich unser Baum. Genau dieses versucht die Funktion randomLevel, und damit kommen wir zum Algorithmus.
Wir benötigen eine Initialisierung des gesamten Systems mittels der Prozedur init_skip-lists. Hier wird nur der Zufallszahlengenerator initialisiert. Es lohnt sich nicht, diese Informationen lokal je „skip list“ zu halten, da wir dann für jede einen solchen benötigten.
Jede aktive „skip list“ benötigt die Verwaltungsstruktur listStructure, die den Startknoten, das zu jeder Zeit maximale Level (wieviele hierarchische Nachfahren-Ebenen existieren noch) und zwei Zeiger auf Funktionen erhält. Sie ermöglichen die unabhängige Gestaltung der „skip list“-Funktionen, so daß mit den gleichen Routinen mehrere unterschiedliche Bäume (z.B. zum Umsortieren) behandelt werden können.
Die Funktion *cmp_fun erhält zwei Informationen als Argumente und muß entscheiden, welches von beiden „kleiner“ als das andere ist, oder ob sie „gleich“ sind. Ihre Rückgabewerte entsprechen im ganzen gesehen denen der Funktion strcmp. Genaueres siehe die Header-Datei „skiplist.h“.
Die Funktion *free_fun erhält eine Information als Argument und entscheidet, was mit ihr nach dem Entfernen aus der „skip list“ geschehen soll.
Das Feld last enthält einen Verweis auf das letzte gesuchte Element. Diese Positionsinformation wird genutzt, um auf die nachfolgenden Informationen zuzugreifen.
Für jede zu speichernde Information benötigen wir einen Zeiger auf die Information und eine sich nach dem Level richtende Anzahl von Zeigern auf die nächsten Informationen. Diese Daten sind in der Struktur nodeStructure gespeichert.
Mittels der Prozedur new_skiplist erzeugen wir eine Verwaltungsstruktur für eine neue „skip list“. Wir benötigen einen Startknoten, l->header, in dem wir nur die Tabelle der Zeiger auf nachfolgende Elemente der verschiedenen Levels speichern. Das Feld l->header.inf bleibt leer. Alle anderen Felder werden mit NULL initialisiert. Dieser Wert indiziert das Ende der Informationsketten.
In die „skip list“ fügen wir Informationen durch die Funktion skip_insert ein. Als Parameter werden die „skip list“, die Information und der Boolsche Wert dp benötigt. Dieser entscheidet, ob doppelte Informationen in der Liste erlaubt sein sollen. Ist der Wert äquivalent zu Null, sind sie nicht erlaubt. Die Funktion sucht, beim maximalen Level beginnend, nach Informationen, deren Schlüssel kleiner als die mitgelieferte Information ist. Übrigens sind die Schlüssel immer Teil der Information. Die Tabelle update enthält in Stelle k die Adresse des letzten Knotens, der „kleiner“ als die neue Information ist. Falls die Information eingefügt werden soll, sind diese Werte an den entsprechenden Stellen zu modifizieren. Es wird „FALSE“ zurückgegeben, falls die Information schon vorhanden war, „TRUE“, falls sie eingefügt werden mußte.
skip_delete löscht eine Information und gibt „TRUE“ zurück, falls der Auftrag ausgeführt, „FALSE“, falls keine Information gefunden wurde. Auch hier wird als erstes nach der Information gesucht, indem man zuerst mit den am weitesten zeigenden Verweisen („k = l->level“) beginnt und schließlich bei den niedrigsten Verweisen endet („k = 0“).
Mit Hilfe von skip_search ist der Zeiger l->last auf einen Teil des Suchbaumes einstellbar, von dem man dann mit skip_next auf die nachfolgenden Elemente zugreifen kann. Wurde die Information nicht gefunden, oder ist das Ende der Informationskette erreicht, wird „NULL“ zurückgeliefert. Ein nachfolgender skip_next-Aufruf beginnt am Anfang der Informationen.
Restriktionen und mögliche Verbesserungen
Nun, es gibt sie doch. Das Verfahren des Zufallszahlengenerators erlaubt eine maximale Hierarchietiefe von 16. Das bedingt, daß der Algorithmus im vorliegenden Fall „optimal“ bis zu einer maximalen Anzahl von 2 hoch 16 unterschiedlichen Informationen funktioniert. Darüber hinausgehende erfolgreiche Einfügungen werden zwar verkraftet, reduzieren aber die Leistungsfähigkeit des Algorithmus’.
Ist die hohe Flexibilität nicht gefordert, lassen sich Vergleichs- und Speicherfreigabefunktionen direkt kodieren. Im vorgestellten Fall werden sie aber über ein Unterprogramm aufgerufen, das die Geschwindigkeit des Algorithmus’ etwas mindert.Die Information läßt sich anstelle einer Verzeigerung auch einfach direkt in node-Structure kodieren, um so einen Effizienzgewinn zu erreichen. Dann allerdings benötigt man für jeden aktiven Baum einen eigenen Algorithmus.
Eine weitere Optimierung besteht in der Definition eines Elements mit einem maximalen Wert, der im Falle von erlaubten Duplikaten oder nicht sicherem Auftreten niemals eingefügt werden darf. Dadurch kann die Abfrage auf „NULL“ ersatzlos gestrichen werden.
Das Programm
Das Beispielprogramm nimmt eine Textdatei als Eingabe und sortiert die darin enthaltenen Wörter (alles, was durch mindestens ein Leerzeichen getrennt ist, führende und abschließende Kontrollzeichen werden ignoriert) in eine „skip list“ ein. Die gesamte Datei wird in den Speicher geladen, um auf zusätzliche malloc-Aufrufe zu verzichten. Ein Aufruf der Funktion „strtok“ modifiziert destruktiv diesen Puffer und separiert so alle gefundenen Wörter.
Ein kleines Schmankerl am Rande: Das Programm schafft es, die deutschen Sonderzeichen ‘ä’, ‘ö’ ‘ü’ und ‘ß’ richtig zu sortieren.
Die gewonnenen Informationen werden, um alle Wörter die mit einem ‘m’ beginnen, vermindert, ausgegeben. Sie könnten jetzt korrekturgelesen werden. Ein paar statistische Informationen, wieviele Knoten sich auf welchen Levels befinden, werden zur Kontrolle ebenfalls geliefert. Level 0 sollte die größte Anzahl Knoten, das größte Level die kleinste Anzahl liefern. Ist dies im Ganzen gesehen nicht der Fall, haben Sie entweder eine der wenigen Ausnahmen gefunden (sehr unwahrscheinlich) oder beim Abtippen einen Fehler gemacht (sehr wahrscheinlich).
Was bringt’s
- Die Routinen sind klein und schnuckelig und portabel; unter Turbo C auf dem Atari belegen sie mit allem drum und dran weniger als 800 Bytes, (vielleicht kann sie ja ein Assembler-Programmierer effizienter gestalten).
- Sie sind universell einsetzbar, da konfigurierbar. Man braucht sie nur einmal im Programm zu haben.
- Sie liefern einen zufällig „ausgeglichenen“ Baum, dem auch intensive Operationen nichts anhaben können.
- Sie sind schnell. Sag’ ich ganz einfach einmal. Lediglich bei der Suchzeit müssen sie im Vergleich zu optimal programmierten, nicht-rekursiven AVL-Bäumen ganz leicht zurückstecken. Rekursive Verfahren schneiden schlechter ab. Einfüge- und Ausfügeoperationen sind jeweils wesentlich schneller. Nähere Informationen dazu kann man in dem unten angeführten Artikel nachlesen.
[1] William Pugh „skip list“s: A probabilistic alternative to balanced trees; Communications of the ACM; June 1990, Vol 33, Number 6
/* Diese Routine lehnt sich an ein Beispiel von
* William Pugh an Er wurde um Funktionalität
* verallgemeinert und anwenderfreundlicher
* gestaltet
*
* Klaus Elsbernd entwickelt mit TURBO C
* (c) 1991 MAXON Computer
*/
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include <skiplist.h>
int randomLevel(void);
int randomsLeft;
long randomBits;
void
init_skiplists () /* --- initialize skip lists */
{
/* get a 32 bits random level number! */
randomBits = (rand()<<16)+rand();
randomsLeft = BitsInRandom/2;
} /* init_skiplists */
int
skip_cmp_default (x,y) /* compares two strings */
char *x, *y;
{
return(strcmp(x,y));
} /* skip_cmp_default */
void /* ----------- don't free the information */
skip_free_default (x)
char *x;
{
return;
} /* skip_free_default */
skip_list /* create a new skip list */
new_skiplist (cmp_fun,free_fun)
BOOLEAN (* cmp_fun)();
void (* free_fun)();
{
skip_list l;
int i;
l = (skip_list)
malloc(sizeof(struct listStructure));
l->level = 0
l->cmp_fun = (cmp_fun != NULL)
? cmp_fun : skip_cmp_default;
l->free_fun = (free_fun != NULL)
? free_fun skip_free_default;
l->header = newNodeOfLevel(MaxNumberOfLevels);
l->last = NULL;
l->no = 0; /* no of entries in the skiplist */
/* If you need information about used memory,
* uncomment the following statement
l->memory = sizeof(struct listStructure)
+ sizeof(struct nodeStructure)
+ (MaxNumberOfLevels)*sizeof(node);
*/
for (i = 0; i < MaxNumberOfLevels; i++)
l->header->forward[i] = NULL;
return(1);
} /* new_skiplist */
void
free_skiplist (l)/* free an allocated skiplist */
skip_list l;
{
register node p, q;
p = l->header;
do {
q = p->forward[0];
/* free the information */
(l->free_fun)(p->inf);
free(p); /* free node storage */
p = q;
} while (p != NULL);
free(l->header); /* free header storage */
free(l); /* free list storage */
} /* free_skiplist */
int
randomLevel () /* --------- get random level */
{
register int level = 0;
register long b;
/* While 2 consecutive bits of a random number
* are 1= 0 add 1 to level;
* It will be very unlikely, that many sequences
* will result in high levels. */
do {
b = randomBits & 3;
if (!b) level++;
randomBits >>= 2;
if (--randomsLeft == 0) {
randomBits = (rand()<<16)+rand();
randomsLeft = BitsInRandom/2;
}
} while (!b);
return(level > MaxLevel ? MaxLevel : level);
} /* randomLevel */
BOOLEAN
skip_msert (1, inf, dp) /* insert information */
register skip_list l;
register Information *inf;
BOOLEAN dp,
{
register int k;
register node p, q;
register int cmp;
node update[MaxNumberOfLevels];
p = l->header;
/* Search first the skip list elements within
* level k using the comparison function
* cmp_fun. Than decrement k down to level 0
*/
k = l->level;
do {
while (q = p->forward[k],
q != NULL
&& (cmp = l->cmp_fun(q->inf,inf))
< 0) {
p = q;
}
update[k] = p;
} while (--k >= 0);
/* If the key is already there and duplicates
* are not allowed, than update the value
*/
if (!dp && q != NULL && cmp == 0) {
/* the last information will be stored */
q->inf = inf;
return(FALSE);
}
l->no++; /* count number of nodes */
/* Generate a new random level for the new key
* and initialize it with the apropnate
* pointers
*/
k = randomLevel();
/* Is the new level
* greater than the old skiplist level? */
if (k > l->level) {
k = ++l->level;
update[k] = l->header;
}
q = newNodeOfLevel(k);
/* If you need information about used memory,
* uncomment the following statement
l->memory += sizeof(struct nodeStructure)
+ (k)*sizeof(node);
*/
q->inf = inf;
do { /* insert the new element */
p = update[k]; /* save old pointers */
q->forward[k] = p->forward[k];
p->forward[k] = q; /* insert the new one */
} while (--k >= 0) ;
return(TRUE);
} /* skip_insert */
BOOLEAN
skip_delete (l,inf) /* delete information */
register skip_list l;
register Information *inf;
{
register int k, m;
register int cmp;
node update[MaxNumberOfLevels],
register node p, q;
p = l->header;
k = m = l->level;
do { /* find the information */
while (q = p->forward[k],
q != NULL
&& (cmp = l->cmp_fun(q->inf,inf)) < 0)
p = q;
update[k] = p;
} while (—-k >= 0);
if (q != NULL && cmp == 0) { /* found? */
/* update all pointers pointing to the
* information to be deleted */
for (k = 0;
k <= m
&& (p = update[k])->forward[k] = q;
k++) {
p->forward[k] = q->forward[k];
}
/* decrease the maximal skip list level,
* if necessary */
while (l->header->forward[m] == NULL && m > 0)
m—-;
l->level = m;
l->no—-;
(l->free_fun)(q->inf);
free(q);
/* If you need information about used memory,
* uncomment the following statement
l->memory -= sizeof(struct nodeStructure)
+ (k)*sizeof(node);
*/
return (TRUE) ; /* true if key not found */
}
else
return(FALSE);/* false if key not found */
} /* skip_delete */
node
skip_search (1, inf) /* ---------- search a key */
register skip_list l;
register Information *inf;
{
register int k;
register int cmp;
register node p, q;
p = l->header;
k = l->level;
do {
while (q = p->forward[k],
q != NULL
&& (cmp = l->cmp_fun(q->inf,inf)) < 0)
p = q;
} while (—-k >= 0);
l->last = q; /* remember last searched cell */
if (q != NULL && cmp != 0)
return(NULL);
return(q);
} /* skip_search */
node
skip_next (l) /* search for next information */
register skip_list 1,
{
if (l->last = NULL)
l->last = l->header;
l->last = l->last->forward[0];
return(l->last);
} /* skip_next */
/* include file for skip-lists *
*
* Klaus Elsbernd TURBO C
* (c) 1991 MAXON Computer
*/
#ifndef Information
/* no already defined by the user */
#define Information char
#endif
#define FALSE 0
#define TRUE 1
#define BOOLEAN int
#define BitsInRandom 31
#define allowDuplicates
#define MaxNumberOfLevels 16
#define MaxLevel (MaxNumberOfLevels-1)
#define newNodeOfLevel(1) (node)malloc(sizeof(struct nodeStructure) + (1)*sizeof(node))
/* 2 structures needed */
typedef struct nodeStructure *node;
typedef struct nodeStructure {
Information *inf;
/* variable sized array of forward pointer */
node forward[1];
};
typedef struct listStructure {
/* Maximum level of the list (1 more, than
* the number of levels in the list) */
int level;
unsigned int no; /* number of nodes in list */
/* pointer to the firstheader */
/* if you need information about used Memory,
* uncomment the following statement
unsigned long memory.
*/
struct nodeStructure *header;
struct nodeStructure *last;
/* pointer to comparasion function with
* two arguments
* cmp_fun returns
* 0 iff argument 1 = argument 2
* 1 iff argument 1 > argument 2
* -1 iff argument 1 < argument 2
*/
int (* cmp_fun)
(Information *x,Information *y);
void (* free_fun)(Information *inf);
} *skip_list;
/* prototypes: */
void init_skiplists (void) ;
skip_list new_skiplist(BOOLEAN (* cmp_fun)(), void (* free_fun)());
void free_skiplist(skip_list l);
int skip_cmp_default(Information *x, Information *y);
void skip_free_default (Information *inf) ;
BOOLEAN skip_insert(skip_list l,
Information *inf,
BOOLEAN dp),
skip_delete(skip_list l,
Information *inf);
node skip_search(skip_list l,
Information *inf),
skip_next(skip_list l);
/* externals: */
extern int skip_cmp_default();
extern void skip_free_default();
extern BOOLEAN skip_insert(), skip_delete();
extern node skip_search(), skip_next();
extern void init_skiplists(), free_skiplist();
extern skip_list new_skiplist();
/* This program read a character file
* and inserts all words, separated by spaces
* into a skip list;
* Then all words are printed on a new line
*
* Klaus Elsbernd TURBO C
* (c) 1991 MAXON Computer
*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
/* Information is a string */
#define Information char
#include <skiplist.h>
/* define german characters: */
#define ae (unsigned char)'\204'
#define Ae (unsigned char)'\216'
#define oe (unsigned char)'\224'
#define Oe (unsigned char)'\231'
#define ue (unsigned char)'\201'
#define Ue (unsigned char)'\232'
#define ss (unsigned char)'\236'
void sortcharupcase(unsigned char * pointer);
int eqlchupper(unsigned char ch1,
unsigned char ch2);
int cmp_str(char *x, char *y);
void /* — prepares character for comparing */
sortcharupcase (ptr)
unsigned char *ptr;
{
unsigned char c;
if ((c = *ptr) >= 'a') {
if (c <= 'z')
*ptr -= 'a'-'A';
else
*ptr = (c == ae || c == Ae)
? 'A' :
(c == oe || c == Oe) ? 'O' :
(c == ue || c == Ue) ? 'U' :
(c == ss) ? 'S' : *ptr;
}
} /* sortcharupcase */
int /* compares 2 characters, if they are eql */
eqlchupper (ch1,ch2)
unsigned char ch1, ch2;
{
sortcharupcase(&ch1);
sortcharupcase(&ch2);
return(ch1 - ch2);
} /* eqlchupper */
int
cmp_str (x, y) /* --------- compares two strings */
register char *x, *y,
{
/* compare strings ignoring
* upper/lower-case differences */
while (*x && *y &&
(!(*x - *y) || !eqlchupper(*x,*y))) {
x++; y++;}
return(eqlchupper(*x,*y));
} /* cmp_str */
void
free_str (x) /* --------- free an information */
char *x;
{
return;
} /* free_str */
int
main (argc,argv)
int argc;
char *argv[],
{
skip_list l;
FILE *file;
long size;
char *buffer, *str;
register node p, q;
int i, k;
long no;
if ((argc != 2) /* argument given? */
|| (file = fopen(argv[1],"r")) == NULL) {
printf("parameter <existing file> required\n");
return(-1);
}
init_skiplists(); /* initialize skip list */
l = new_skiplist(cmp_str,skip_free_default);
/* determine the length of the file */
if (fseek(file,01,SEEK_END) != 0) {
printf("error at positioning at end\n");
return(-1);
}
size = ftell(file); /* size of the file */
fseek(file,01,SEEK_SET);
/* allocate enough buffer for the file */
str = buffer =(char *)malloc((size_t)(size+1));
/* read all lines, and separate them by ' ' */
while (fgets(str,(int)size,file) != NULL) {
str += strlen(str)-1;
*str++ = ' ';
}
fclose(file);
/* tokenize the input file and put the token
* in the tree */
no = 0; /* number of insert operations */
for (str = strtok(buffer," ");
str != NULL;
str = strtok(NULL," ")) {
/* skip most of non literal characters */
for (; *str != '\0'
&& ((unsigned)(*str) < 'A');
str++);
for (i = (int)strlen(str)-1;
i > 0
&& ((unsigned)(*(str+i)) < 'A');
i--)
*(str+i) = 0;
no++;
skip_insert(1, str, FALSE);
}
/* provide same statistic information */
for (k = l->level; k >= 0; k—-) {
p = l->header;
i = 0;
while (q = p->forward[k], q != NULL) {
p = q;
i++;
}
printf("No of nodes in level %d: %d\n",k,i);
}
if (i != l->no)
printf("illegal number of nodes\n");
printf("Number of inserted strings %ld\n",no);
/* delete all strings
beginning with an 'm' or 'M' */
if ((p = skip_search(l,"M")) == NULL)
p = skip_next(l);
for (; p != NULL
&& cmp_str(p->inf,"N") < 0;
p = q) {
q = skip_next(l);
skip_delete(l,p->inf);
}
/* print the contents of the skip list
* in sorted order */
p = l->header->forward[0]; /* first element */
while (p != NULL) {
printf("%s\n",p->inf);
p = p->forward[0];
}
free_skiplist(1); /* obvious */
return(0);
) /* main */