
Oft handelt es sich bei der Schreibarbeit am Computer um die Erstellung längerer Dokumente, die evtl, sogar veröffentlicht werden sollen. Da hierbei einiges benötigt wird, was eine normale Textverarbeitung nicht bereitstellt, löst man solche Aufgaben am besten mit sog. Textsatz- oder Formatierungsprogrammen.
Eines der wohl leistungsfähigsten Programme dieser Art ist TeX. Es existiert für die unterschiedlichsten Computersysteme und arbeitet nach dem Prinzip eines Compilers. Man erzeugt mit seinem Lieblingseditor einen ASCII-Text, der von TeX dann zu einem perfekt gesetzten Dokument übersetzt wird.
Die Arbeit zur Erzeugung von Inhalts-, Literatur- und Abbildungsverzeichnissen oder zur Erstellung von Seiten- und Formelnummerbezügen wird dabei vom Programm selbständig erledigt. Dabei berücksichtigt TeX Regeln, die seit Gutenberg von professionellen Layoutern verfeinert und festgelegt wurden. TeX ist also nicht mit einer Schreibmaschine, sondern eher mit einer Druckerei zu vergleichen.
Naturwissenschaftler, die Studien-, Diplom- oder Promotionsarbeiten zu erstellen haben, wissen ein Lied davon zu singen, wie arbeitsintensiv die Erstellung von Formeln innerhalb eines Textes sein kann. Entweder man benutzt seine Lieblingstextverarbeitung und trägt die Formeln nachträglich mit Hilfe einer Schablone ein, oder man investiert einiges an Zeit, um mit dem WYSIWYG-Verfahren das Gewünschte zu erzeugen. Nach Murphy’s Law wird übrigens beim Seitenumbruch diese Arbeit wieder zunichte gemacht, da die Seite genau auf dem Bruchstrich getrennt wird. An eben dieser Stelle beweist TeX eine seiner Stärken. Mathematische Formeln können nicht nur perfekt gesetzt werden, sondern TeX weiß auch, daß diese Gebilde beim Seitenumbruch gesondert behandelt werden müssen. Durch diese und viele andere Fähigkeiten ist TeX ein optimales Instrument zur Erstellung von längeren Texten.
Um diejenigen, die TeX noch nicht kennen, neugierig zu machen, möchte ich anhand einiger Beispiele auf eine besondere Stärke des Programmes hinweisen.
Wie schon erwähnt, erstellt man seinen Text im ASCII-Format und läßt ihn dann von TeX in das gewünschte Dokument übersetzen. Um dem Programm mitzuteilen, welche Textabschnitte als Formel gesetzt werden sollen, schließt man sie in sog. Umgebungen ein. Dies erreicht man z.B. mit den Befehlen:
\begin {displaymath}
Formeltext
\end{displaymath}
was eine vom Text abgesetzte Formel ergibt, oder mit den Befehlen
\begin{math}
Formeltext
\end{math}
welche dafür sorgen, daß die Formel innerhalb der laufenden Textzeile gesetzt wird.
Wer seine Formeln fortlaufend numerieren möchte, erreicht dies mit der Umgebung:
\begin{equation}
Formeltext
\end{equation}
Gibt man seiner Formel mit \label{Name} einen Namen, kann man im laufenden Text mit \ref{Name} Bezüge auf die entsprechende Formelnummer herstellen, ohne sie vorher zu kennen. Dies ist eine große Arbeitserleichterung beim nachträglichen Einfügen von Formeln, da TeX selbständig sämtliche Nummern und Nummernbezüge ändert.
Wer jetzt allerdings enttäuscht ist über die Notwendigkeit, Befehle lernen zu müssen, sollte trotzdem weiterlesen, da man die Tipparbeit auch verkürzen kann. Zum einen hält das zu TeX gehörende Makropaket LaTeX einige Abkürzungen bereit, zum anderen kann man ja die Funktionstasten seines Editors mit den wichtigsten Befehlen belegen.
Weitere sehr nützliche Tips dazu stehen übrigens in der ST-Computer 4/91 ‘Tempus für TeX und Fortran’.
Wer mit den Abkürzungen $ 3+b=5 $ eine Textformel, oder mit $$ x-y=5 $$ eine abgesetzte Formel erzeugt, wird schnell feststellen, daß TeX bzw. LaTeX Zahlen (Konstanten) in der Schriftart ‘roman’ und Buchstaben (Variablen) in der Schriftart ‘italic’ setzt, was übrigens einem weltweiten Standard entspricht.
Mathematisches
Selbstverständlich läßt sich mit TeX eine Vielzahl von Sonderzeichen darstellen. Befindet man sich innerhalb einer mathematischen Umgebung, erhält man z.B. das griechische Alphabet durch Ausschreiben der gewünschten Symbole, mit einem vorangestellten ‘/’ (\alpha, \beta, \gamma usw.).
Beginnt der Symbolname mit einem Großbuchstaben, erhält man den entsprechenden griechischen Großbuchstaben (\Delta, \Theta, \Omega usw.).
Hoch- und Tiefstellungen für jeweils ein Zeichen erreicht man durch Voranstellen von ‘^’ und ‘’. Dabei werden Exponenten durch ‘^’ und Indizes mit ‘’ erzeugt. Möchte man mehrere Zeichen hoch- oder tiefstellen, setzt man das Gewünschte in geschwungene Klammern ‘_{max}'.
Die eigentlichen Stärken des Formelsatzes werden aber beim Erzeugen von Brüchen oder Wurzeln deutlich. TeX weiß selbst, wie lang der Bruchstrich sein muß bzw. wie das Wurzelzeichen zu dimensionieren ist. Kurze Brüche, die innerhalb einer Textzeile gesetzt werden sollen, trennt man einfach mit einem ‘/’, bei abgesetzten Brüchen dagegen verwendet man den Befehl:
\frac{ Zähler }{ Nenner }
Hat man eine Funktionstaste mit dem Befehl belegt, muß man nur noch die Klammem für den Zähler und den Nenner ausfüllen. Dabei ist es TeX egal, ob man jedes Zeichen in eine Zeile schreibt oder überhaupt keine Leerzeichen verwendet (siehe Beispiel 1).
Das Erzeugen von Wurzeln in der richtigen Größe ist ähnlich einfach. Für eine Quadratwurzel benötigt man lediglich den Befehl:
\sqrt{ }
Wurzeln höherer (n-ter) Ordnung erhält man durch:
\sqrt[n]{ }
Richtig interessant wird es aber, wenn man die Befehle für Brüche und Wurzeln in beliebige Tiefe schachtelt (siehe Beispiel 2).
Man beachte, daß TeX für die Brüche im Zähler des Hauptbruches eine kleinere Schriftart wählt.
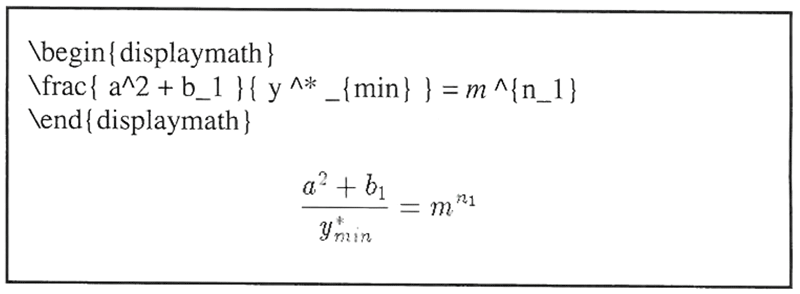 Beispiel 1
Beispiel 1
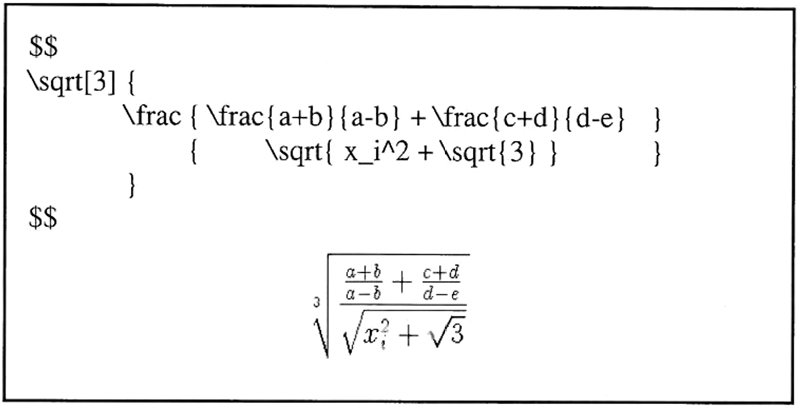 Beispiel 2
Beispiel 2
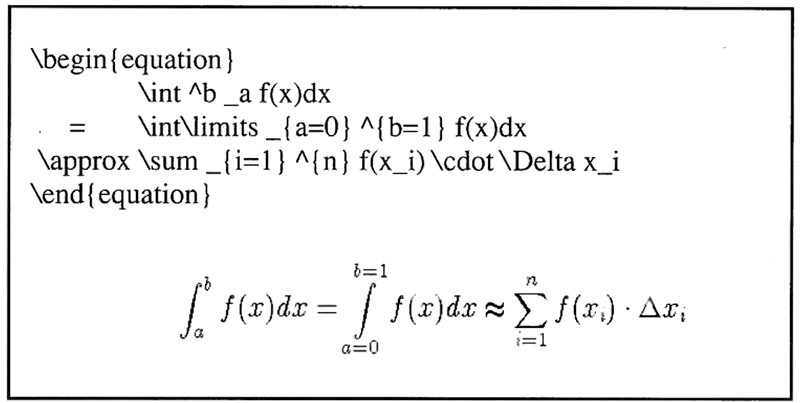 Beispiel 3
Beispiel 3
 Beispiel 4
Beispiel 4
Summen- und Integralzeichen
Die Befehle für ein Summen- oder Integralzeichen sind leicht zu merken, sie lauten:
\sum bzw. \int
Möchte man die Summations- bzw. Integrationsgrenzen dazuschreiben, benutzt man wieder ‘^’ für die obere und ‘_’ für die untere Grenze. Für Hoch- und Tiefstellungen mehrerer Zeichen gilt das gleiche wie bei längeren Exponenten oder Indizes.
Bei der Plazierung der Grenzen ist jedoch folgendes zu beachten. Handelt es sich um eine Textformel, werden die Grenzen rechts neben das jeweilige Symbol geschrieben. Handelt es sich um eine ab-gesetzte Formel, landen die Grenzen über und unter dem Summenzeichen, jedoch ebenfalls rechts vom Integralzeichen. Möchte man dies ändern, verwendet man für die Integrationsgrenzen den Befehl:
\int\limits^b_a
Wer jetzt verwirrt ist, kann sich anhand von Beispiel 3 Klarheit verschaffen.
Es würde den Rahmen dieses Artikels sprengen alle von TeX bzw. LaTeX bereitgestellten Symbole und Formatierungsmöglichkeiten aufzuzählen. Denjenigen, die mit allen Möglichkeiten dieses Programmes richtig arbeiten wollen, empfehle ich das Buch von Helmut Kopka [1] oder die Kurzbeschreibung von Hubert Parti, diejederTeX-Version beiliegen sollte.
Matrizen und Vektoren
Wie ich schon gezeigt habe, lassen sich die Befehle zur Erzeugung von Brüchen und Wurzeln beliebig schachteln. Eine weitere Spezialität von TeX ist die Formatierungshilfe für Tabellen. Diese wird in der mathematischen Umgebung zum leichten Setzen von Vektoren oder Matrizen benutzt.
Man teilt TeX dazu lediglich mit, wieviel Spalten die Matrix bekommen soll und wie die Zeichen innerhalb der Spalten angeordnet werden sollen (1 linksbündig, r rechtsbündig, c zentriert),
Um drei Spalten zu bekommen, in denen zentriert angeordnet wird, benötigt man innerhalb einer mathematischen Umgebung lediglich den Befehl:
\begin{array} {ccc}
Die notwendige Spaltenbreite ermittelt TeX anhand des breitesten Spalteneintrages selbständig. Von Spalte zu Spalte gelangt man mit ‘&’ und eine Zeile wird mit ‘\Y abgeschlossen. Die letzte Zeile der Matrix wird allerdings nicht mit ‘\Y abgeschlossen, sondern mit
\end{array}
OK, hier wird es jetzt etwas schwieriger, aber Beispiel 4 sollte für Durchblick sorgen.
$$
\begin {array} {ccccc}
\left(
\begin {array}{c}
v_1(p)\\
v_2(p)\\
\vdots \\
v_n(p) \\
\end {array}
\right)&
= &
\left(
\begin{ array} {c}
p_1(x)\\
p_2(x)\\
\vdots \\
p_n(x)\\
\end{array}
\right)&
\cdot &
\left(
\begin{array}{cccc}
d_{ 1,1} & d_{ 1,2} &\ldots & d_{1,n} \\
d_{ 2,1} & d_{ 2,2} &\ldots & d_{2,n} \\
\vdots & \vdots & \ddots & \vdots \\
d_{n,1} &djn,2} &\ldots & d{n,n} \\
\end {array}
\right)
\end{ array}
$$
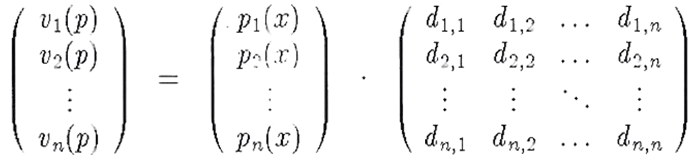 Beispiel 5
Beispiel 5
Siehe Gleichung \ref{test} ).
\begin{eqnarray}
h^3\:-\:
\underbrace{\frac{ 12\cdot\bar U\cdot\eta} {dp/dx}}_{ p’} \cdot h \:+\:
\underbrace{\frac{ 12\cdot\bar U\cdot\eta\cdot h_0} {dp/dx}}_{ q’ } \:=\:0
\label {test}
\end {eqnarray}
Siehe Gleichung (2)
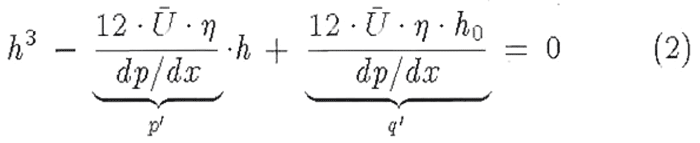 Beispiel 6
Beispiel 6
\psi = \arccos \left(
\frac{ -\frac{ q' }{ 2 } }{\sqrt{\left(\frac{|p’|}{3}\right)^3 } }\right)
$$
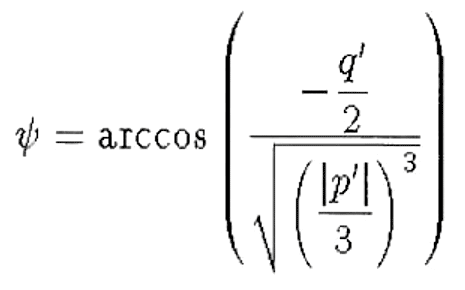 Beispiel 7
Beispiel 7
\begin{eqnarray}
\begin {array}{11}
\displaystyle \int\limits_a^b f(x) dx \approx \quad
\displaystyle \left. \frac {b - a} {6 \cdot n} \cdot \right( f(a) + f(b)
& \displaystyle + 2\cdot\sum_{k=1}^{n-1} f(2k\cdot\Delta x)\\
& \left. \displaystyle + 4\cdot\sum_{k=1}^n f((2k-1) \cdot \Delta x )
\right)
\end {array}
\end{eqn array}
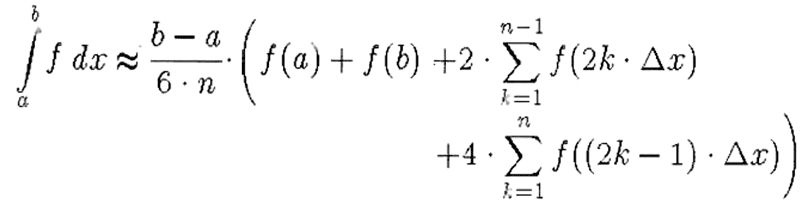 Beispiel 8
Beispiel 8
In Beispiel 5 möchte ich noch zeigen, wozu eine geschachtelte ‘array’-Umgebung in der Lage ist. Die Befehle ‘\left(‘ und ‘\right)’ sorgen übrigens für die runden Klammern in der richtigen Größe.
Wie schon gezeigt, bestimmt TeX die Länge von Bruchstrichen und Wurzeln selbständig. Daß die Größe von Klammern von TeX ebenfalls selbständig ermittelt wird, wird anhand der Beispiele 7 und 8 deutlich, in denen die Befehle ‘\left(‘ und ‘\right)’ für unterschiedlich große Klammem sorgen.
Die Fähigkeit, Längen selbständig zu ermitteln kommt auch bei dem Befehl ‘\underbrace{ Bereich }_{ Name }' zum Einsatz. Mit ihm kann man einen Bereich mit einer Klammer unterlegen und ihm einen Namen zu weisen.
In Beispiel 6 wird auch deutlich, was notwendig ist, um Formelbezüge zu erstellen.
Auf einige Besonderheiten in Beispiel 8 sollte ich noch hinweisen. Die Befehle für eine linke und eine rechte Klammer müssen immer paarweise erfolgen. Da die linke Klammer in Beispiel 8 allein innerhalb einer Formatspalte steht, kann man sich mit ‘\left.’ und ‘\right(‘ helfen, da durch ‘\left.’ kein Zeichen gesetzt wird.
Mit dem Befehl ‘\display style’ wird innerhalb einer Formel Umgebung eine größere Schriftart gewählt, und die Befehle ‘\quad’ sowie ‘:’ sorgen für zusätzliche Abstände zwischen den Zeichen.
Abschließend bleibt mir noch zu sagen, daß dies natürlich nur ein kurzer Einblick in die Möglichkeiten der Text- und Formelgestaltung mit TeX war. Neben dem leistungsstarken Formelsatz hat das Programm noch viele andere Fähigkeiten. Evtl, sind ja einige Leser neugierig geworden und fragen sich, warum sie dieses Programm noch nicht besitzen, und was es wohl kosten mag.
In diesem Fall gibt es noch die unglaublich gute Nachricht, daß TeX als Public Domain- bzw. Shareware-Programm zu erhalten ist und somit den Geldbeutel nicht beutelt. Eine Version gibt es gleich ein paar Seiten weiter in der PD-Abteilung und eine bei Stefan Lindner [2].
Wer erst einmal etwas vertraut geworden ist mit TeX, wird sich ganz leicht von seiner WYSIAYG (What You See Is All You Get)-Textverarbeitung trennen können.
Literatur:
[1] Helmut Kopka, „LaTeX - Eine Einführung“, Addison-Wesley, ISBN 3-89319-199-2
[2] Stefan Lindner, Iltisstraße 3, W-8510 Fürth