Schon in der fünften Folge von Algorithmen & Datenstrukturen, behandelte ich eine spezielle Baumstruktur, die gegen Degenerierung geschützt ist: den AVL-Baum. In der heutigen Folge, werde ich Ihnen eine ebenso geschützte Struktur vorstellen: den Bayer-Baum, oder kurz B-Baum.

Noch'n Baum, wieso?

Alle bisher betrachteten Bäume entstammen der Gattung Binärbäume, da sie maximal zwei Nachfolger je Knoten besitzen. Was von der Struktur sehr schön, weil einfach, ist, hat einen großen Nachteil:

Wird wegen hohem Datenaufkommen eine Baumrepresentation auf Massenspeichern gewählt, so sind Binärbäume in hohem Masse uneffektiv, da mit jedem Dateizugriff nur jeweils ein Knoten mit einem Schlüsselelement in den Hauptspeicher geladen wird.

Abhilfe kann man sich verschaffen, indem man mehr als einen Schlüssel in jeden Knoten aufnimmt.

Bezeichnung: Der Baum wird dann von einem Binärbaum zu eine Multiwegbaum. Die Knoten werden als Seiten bezeichnet. Als Blattseiten bezeichnen wir die Seiten, die keine Nachfolger besitzen. Die erste und oberste aller Seiten bezeichnen wir als Wurzelseite.

Dabei wird davon ausgegangen, daß die Schlüssel auf jeder Seite, entsprechend der Schlüsselrelation angeordnet sind. Ist nun, auf der besuchten Seite, der erwünschte Schlüssel nicht auffindbar, so kann er, sofern es sich bei der Seite nicht um eine Blattseite handelt, zwischen seinem unmittelbaren Vorgänger und seinem unmittelbaren Nachfolger gesucht werden. Zwei Spezialfälle gilt es dabei zu beachten: Zum einen können alle Schlüssel der Seite größer sein, als unser gesuchter Schlüssel. In diesem Fall ist 'links' vom ersten (kleinsten) Schlüssel weiterzusuchen. Analog können alle Schlüssel kleiner sein als der Gesuchte. Hier ist 'rechts' vom letzten (größten) Schlüssel weiterzusuchen.

Einige grundsätzliche Überlegungen

Leicht erkennt man, daß ein Baum mit m Schlüsseln maximal m+1- Nachfolger besitzen kann. Ebenso leicht ist einzusehen, daß eine gewisse Obergrenze für die Füllung der Seiten vorzugeben ist, da man sonst nicht wüßte, ob man einen zusätzlichen Schlüssel in die Seite aufnehmen soll, oder ihn auf die Baumnachfolger verweist. Eine andere Überlegung führt zu den Definitionen des Herrn Bayer:

Unsere Multiwegbäume neigen nämlich dazu, genau so leicht zu degenerieren, wie Binärbäume ohne Ausgleichsmechanismen. Deshalb werden, ähnlich den AVL-Bäumen, einige Limitierungen eingeführt, deren Beachtung die Degenerierung von Multiwegbäumen verhindert.

1. Es wird die Ordnung n eines Baumes definiert.
2. Sämtliche Seiten, mit Ausnahme der Wurzelseite, müßen zwischen n und 2n Elementen besitzen.
3. Jede Seite ist Blattseite, oder besitzt genau m+1 Nachfolger, wobei m die Anzahl der Schlüsselelemente der Seite ist.
4. Alle Blattseiten liegen auf einer Höhe.

Datenbankcharakter

Um Ihnen heute eine möglichst effektive Struktur an die Hand zu geben, ist es notwendig, auf die Besonderheiten von Datenbanken, die ja wohl das Hauptanwendungsgebiet von Indexstrukturen sind, einzugehen.

Zunächst einmal: Zeigerstrukturen sind heute out. An ihre Stelle tritt der direkte Random-Access-Zugriff auf Diskettendatei. Was also in den letzten Folgen ein Pointer war, wird nun zu einer Recordnummer, also einer Zahl die den bezeichneten Datensatz in einer Diskettendatei charakterisiert. Eine weitere Besonderheiten ist die strikte Trennung zwischen Daten und Schlüsseln, worunter deren Abspeicherung in unter-schiedlichen Dateien zu verstehen ist.

Grundsätzlich zu Random-Access unter Pascal+

Da Random-Access, wie oben gefordert, vom Vater Pascal's, Niklaus Wirth, nicht vorgesehen war, weichen wir heute ein wenig vom Standard ab. Entgegen der normalen Dateibehandlung in Pascal, nach der eine Datei nur streng sequenziell, will sagen Datensatz für Datensatz abgearbeitet werden kann, bietet Random-Access, wie schon der Name sagt, wahlfreien Zugriff auf alle Datensätze der bezeichneten Datei.

Dies geschieht unter Pascal+ wie folgt: Eine Random-Access-Datei wird unter Pascal+ mit der reset- Standardprozedur zum Lesen und Schreiben geöffnet. Den beiden Standardoperationen get und put wird nun, als zusätzlicher Parameter, eine Recordnummer nachgestellt, die den ent-sprechenden Datensatz kennzeichnet. Zu beachten ist dabei, daß man bei den beiden Operationen nicht über das Dateiende hinausschießen sollte, also auf nicht vorhandene Elemente zugreift. Lediglich erlaubt ist ein schreibender Zugriff mit put auf ein Element, was eine Position außerhalb der Datei liegt, also das Anhängen eines neuen Elementes. Erschwert wird die Sache ein wenig dadurch, daß es seitens Pascals keine Prozedur gibt, mit der man die Recordanzahl bestimmen kann. (Zumindestens habe ich keine gefunden.)

Ohne Dokumentation, gebe ich Ihnen deshalb die Funktion dateilaenge (Listing 6b, Zeilen 28-72) an die Hand, mit der man, unter Angabe eines Dateinamens, der übrigens auch Wildcards beinhalten darf, die erforderlichen Daten erhält. Die Dateilänge wird dabei, per call-by-reference, als zweiter Parameter zurückgegeben. Als bool'schen Rückgabewert der Funktion erhält man ein Flag, was das Vorhandensein der Datei beschreibt. Dividiert man nun die Dateilänge durch das Format des Datentyps (sizeof(<Datentyp>), so erhält man die Anzahl der Datensätze in der bezeichneten Datei. Wird noch der Recordoffset (Position des ersten Records. In Pascal+ die Position 0) in Random-Access-Dateien beachtet, so ist vom erhaltenen Wert noch eins abzuziehen, um den letzten Datensatz zu markieren.

Oder etwa nicht ?

Eine Kleinigkeit gilt es noch zu beachten: Es besteht nämlich ein Unterschied zwischen der virtuellen Datei (Menge der geschriebenen Daten) und der physikalischen Datei (Daten die auf dem Massenspeicher schon angekommen sind.).

Der Unterschied besteht genau im, von Pascal+ benutzten, Puffer für Dateizugriffe. Hier können nämlich noch Datensätze 'rumliegen', die noch nicht geschrieben wurden und auf eine größere Sendung warten, um effektiv weggeschrieben zu werden. Dieser an sich recht löbliche Effektivitätsgrundsatz, führt für unsere Belange dazu, daß aus der physikalischen Dateilänge nicht immer die Anzahl der Datensätze berechnet werden kann. Dieses kleine Problemchen läßt sich auf zwei Arten umgehen: Entweder wird die Diskettendatei, vor jeder dateilaenge-Ausführung, mit close explizit geschloßen, womit wir Pascal den Befehl geben seinen Dateipuffer zu leeren, oder die Anzahl der Datensätze wird nur bei der Initialisierung 'hart' ermittelt und in einer Variable abgespeichert. Im späteren Verlauf muß man dann nur die Variable entsprechend ändern. (Mit letzterer Variante werden wir uns auch rummühen.)

Beim Ausfügen aus Random-Access-Dateien ist zu einem kleinen Trick zu greifen. Das Ausfügen eines einzelnen Datensatzes aus einer Datei ist, wegen den dabei nötigen Datenverschiebungen, sehr uneffektiv. Deshalb nimmt man in sämtliche Datensätze ein zusätzliches Flag auf, um gelöschte Datensätze markieren zu können. Beim Einfügen ist dieses Flag auf true zu setzen und beim eigentlichen Löschvorgang auf false. Durch einen speziellen Packalgorithmus, kann man, nachdem mehrere Einträge gelöscht wurden, die gültigen Daten (flag auf true) zusammenfassen und die ungültigen aus der Datei entfernen.
Doch dazu später mehr.

Typstruktur

Welche Typen aus den unterschiedlichen obigen Überlegungen resultieren, sehen Sie im Listing 6a). Da wären zunächst die beiden Typen key_type und data_type, die unseren normalen Typzerfall in Schlüssel und Daten symbolisieren. Die beiden Typen page_ptr und data_ptr sind nur noch der Bezeichnung nach als Zeiger zu erkennen. Sie symbolisieren den Zeigercharakter, den man mit Verweisen auf Recordnummern erreicht, auch ohne Zeiger explizit anzugeben. Der nächste Typ, base_type, entspricht den Einträgen der Datenbank. Er beinhaltet sämtliche Typen (key & data), die es diesmal zu verwalten gilt. Weiterhin ist hier noch ein Zeiger next vorgesehen, der es uns, wie schon bei den Bäumen, erlaubt Schlüsselgleichheit zu verarbeiten. Zusätzlich ist noch das oben erwähnte Archivierungsflag aufzunehmen.

Die Seiten der Indexdatei, page_type, sehen etwas komplizierter aus. Sie beinhalten zunächst auch ein Archivierungsflag. Die nächste Variable, anz, gibt den Füllungsgrad der Seite an. ptr0 ist der äußerste linke Zeiger der besprochenen Baumstruktur. Die Schlüssel (key), ihre jeweiligen rechten Nachfolger (ptr), und die Zeiger auf die entsprechenden Datensätze in der Datenbank (record_nr), sind zusätzlich in einer Eintragsstruktur item_type zusammengefaßt. Von diesen 'Einträgen' benötigen wir maximal Baumordnung mal zwei, also 1..nn Stück. Es bietet sich eine ARRAY- Representation an, die Sie hier auch realisiert finden.

Beide Seitenarten sind nun noch global (!) als FILE OF ... zu deklarieren, wobei die unterschiedlichen Intentionen in die Namenswahl eingehen (Listing 6c, Zeile 20+21).

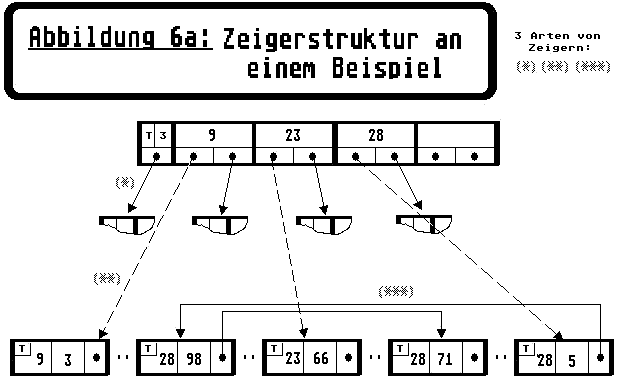
Ein kleines Beispiel für eine B-Baumstruktur zweiten Grades, mit Verzeigerung in die Datenbanken, finden Sie in Abbildung 6a). Die ()-Zeiger stellen dabei die Verzeigerung der Indexseiten dar. Die ()-Zeiger symbolisieren die Zeiger von der Indexdatei zur Datenbank. Und, last but not least, zeigen die ()-Zeiger die Verknüpfung innerhalb der Datenbank, zwecks Organisierung der Elementnachfolgerliste.

Wie weiter oben bereits angeklungen ist, benötige ich heute auch einige Konstanten.

Eine zusätzliche Präprozessor- Datei, für die Konstanten, möchte ich Ihnen allerdings ersparen, zumal es mit Pascal+ ab Version 2.0 möglich ist Konstanten-, Typ-, und Operationsdefinitionen wild zu mischen.

Für die B-Baumkonstanten bemühen Sie also jetzt bitte unser heutiges Demoprogramm (Listing 6c, Zeilen 11-14). Die Konstante n beinhaltet den Baumgrad; nn den doppelten Baumgrad. Als Ersatz zur Konstante nil bei Pointern, führe ich heute die Konstante leer für ein nicht spezifiziertes Random-Access-Element ein. Weiterhin treffe ich die Konvention, daß das B-Baumwurzelelement immer in erster Dateiposition (0) anzutreffen ist, um mir eine zusätzliche Informationsdatei zu ersparen. Daher noch eine kleine Konstante, wurzel, zwecks besserer Lesbarkeit.

Die Operationen auf B-Bäumen im einzelnen (Listing 6b, ab Zeile 74):

create_database

Die Indexdatei und die Datenbank werden mit rewrite eröffnet, um sie neu zu erzeugen und dabei gegebenenfalls alte Inhalte zu löschen.

start_database

Zunächst werden die beiden Dateienderecords ermittelt (last_index und last_data). Auf das darauffolgende Öffnen der beiden Dateien zum Random-Access-Zugriff (reset), erfolgt noch eine Fallunterscheidung, die zwischen einer leeren Datei und einer Datei mit mindestens einem Element unterscheidet. Entsprechend dem Ergebis dieser Fallunterscheidung, ist der Anker unseres B-Baumes (tree) entweder auf leer, oder auf wurzel zu setzen.

insert_data

Den Kern von insert_data bildet die Prozedur search. Mit ihr wird, ähnlich der Suche in Binärbäumen, eine rekursive Suche in den B-Bäumen durchgeführt. Anders als bei den Binärbäumen sind allerdings je Seite maximal nn Wegentscheidung zu treffen. Da nn frei wählbar und so mitunter recht groß werden kann, bietet es sich an, eine binäre Suche auf dem Schlüsselarray item durchzuführen (Zeilen 189-197). Ist das Element gefunden worden (Zeile 198: l-r>1), dann ist am B-Baum keine Änderung vorzunehmen. Das neue Element ist lediglich am Anfang der Nachfolgerliste in die Datenbank einzuhängen (Zeilen 200-205). Andernfalls geht die rekursive Suche weiter (Zeilen 209-212), bis die rekursive Abbruchbedingung (Zeile 174) erfüllt ist. Da uns die B-Baumdefinition Nummer 4 ein Einfügen unterhalb einer Blattseite verbietet, wird der neue Wert über den Parameter v von search zurückgegeben. Der Wert true des Parameters h symbolisiert dabei, daß ein Wert über den Parameter v zurückgereicht wurde und in einer höheren Seite einzufügen ist. Dies geschieht durch Check auf h nach dem rekursiven Aufruf von search (Zeile 213). In diesem Fall wird die Prozedur insert aufgerufen, die das Einfügen von v in die entsprechende Blattseite ausführt und gegebenenfalls, bei wiederholtem Seitenüberlauf, einen neuen Wert für v bestimmt. Im nicht-trivialen Fall des Seitenüberlaufs (Zeilen 136-170) werden dabei einige Eintragsshiftereien vorgenommen, deren ge-naues Studium ich dem interessierten Leser überlassen möchte, da die Details diesen ohnehin recht großen Beitrag wahrscheinlich sprengen würden.

Im Rumpf der Prozedur insert_data wird, vor dem Aufruf von search, zunächst der Datenbankpuffer initialisiert und am Ende der Datenbank eingehängt. Dabei ist darauf zu achten, daß zuvor die Datensatzanzahl, last_data, inkrementiert wurde. Nach dem Aufruf von search besteht nun noch die Möglichkeit, daß sich noch ein Element in v befindet (Zeilen 231-249). Dieses Element wird dann das erste Element der neuen Baumwurzel. Hierbei haben wir auch noch darauf zu achten, daß unserer Vereinbarungen, die Wurzel betreffend (Wurzel ist immer in Position 0) eingehalten werden. Diese Begebenheit macht normalerweise die Vertauschung von zwei Indexseiten notwendig.

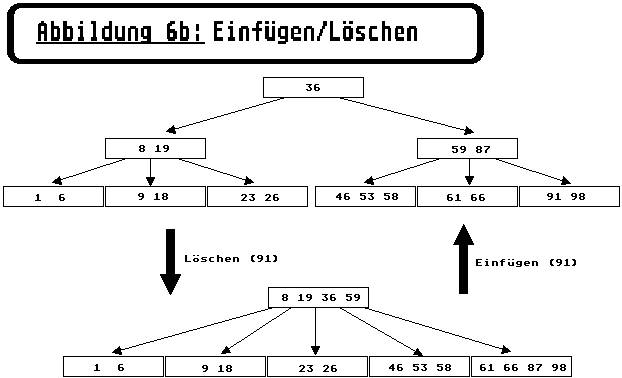
Einen allgemeinen Fall für das Einfügen (und auch Löschen) eines Elementes in einem B-Baum zweiten Grades, finden Sie in Abbildung 6b). Unser Algorithmus versucht das neue Element (91) zunächst in die äußerste linke Seite einzufügen. Da diese aber schon voll ist (Grad * 2 = 4), wird die Seite aufgeteilt. Das mittlere Element der alten Seite (87) wandert dabei über den Parameter v unseres Algorithmus zurück und wird als Entscheidungselement für die beiden neuen Seiten (61 66 / 91 98) in die obere Seite übernommen. Hier wird dadurch wiederum ein Überlauf ausgelöst, der letztendlich zu einer Steigerung der Baumhöhe führt, indem eine neue Wurzelseite (36) angelegt wird.

Anmerkung: Die Random-Access-Struktur ist leider nicht ganz so pflegeleicht, wie unsere bisherigen Zeigerstrukturen. Deshalb muß man beim Arbeiten mit Random-Access sehr darauf bedacht sein, den Inhalt der Puffervariablen rechtzeitig (vor eventuellen Änderungen) wegzuschreiben (put), um fehlerhafte Variablenbelegungen zu vermeiden. Die entsprechenden Programmstellen wirken dadurch allerdings nicht ganz so elegant, wie Sie das bisher gewohnt waren. Nicht bei insert, aber in einigen der nun folgenden Operationen wird sogar das Anlegen von Kopien der Puffervariablen notwendig, nämlich genau dann, wenn auf mehrere der Indexseiten zugegriffen werden muß.

delete_data

delete_data besitzt mit der Prozedur search einen Programmteil, der sich durch sehr ähnlichen Aufbau die Namensgleichheit mit der Prozedur 'search' unter insert_data verdient. Es wird hier ebenfalls der rekursive Baumdurchlauf betrieben, nur das bei der Auffindung, bzw. Nichtauffindung eines Elementes andere Konsequenzen gezogen werden müßen.

Wird ein Element nicht gefunden (Zeile 399, a=leer), dann ist der Job für delete_data erledigt, was Sie an den durchweg negativen Bekundungen in den Zeilen 401-403 leicht feststellen (false/leer/false). Andernfalls ist unser Problem nicht so einfach.

Grundsätzlich haben wir beim Ausfügen aus Bayer-Bäumen eine ähnliche Situation, wie beim Ausfügen aus den schon hinreichend bekannten Binärbäumen. Der einfachste Fall, der auftreten kann, ist das Ausfügen aus einer Blattseite (Zeilen 428-432). Hier muß eben nur die Seite entsprechend zusammengerückt werden. Befindet sich unser auszufügendes Element nicht auf einer Blattseite, so ist es, genau wie bei den Binärbäumen durch den unmittelbaren Vorgänger, oder Nachfolger in der Relation zu ersetzen. Der Abwechslung halber nehmen wir diesmal nicht den maximalen linken Nachfolger des rechten Blattelementes (lexikographische Nachfolger), sondern den maximalen rechten Nachfolger des linken Blattelementes (lexikographischen Vorgänger). Diesen ermittelt uns die, in ähnlicher Form schon häufig benutzte, Prozedur del, die auf rekursiven Wegen die Nachfolgerliste hinabsteigt. Unten angelangt (q=leer; Bedingung in 399; Ausführung in 386-393) ist der k-te Eintrag des Elementes a durch den letzten Eintrag der ermittelten Blattseite p zu ersetzen. Anders als bei den Binärbäumen brauchen wir uns diesmal nicht um einen eventuellen Nachfolger des letzten Eintrages von p zu kümmern, den der existiert ja, laut B-Baumdefinitionen, nicht.

Die Krone der Unübersichtlichkeit wird nun von der Prozedur underflow erreicht, die benutzt wird, um Seiten mit weniger als n Blattelementen wieder aufzufüllen, bzw. mit anderen Seiten zusammenzulegen. Sie wird immer dann angewandt, wenn man aus einem rekursiven Aufruf, entweder von search, oder von del zurückkommt und der Parameter h true ist und somit einen Unterlauf in der zurückgelassenen Seite aufweist. In diesem Fall ist der Prozedur underflow die Seite mit Unterlauf, a, deren Vorgänderseite, c und die Eintragposition s mitzuteilen, die die genaue Stelle in c markiert, deren Nachfolger a ist. Die Seite b stellt nun den anderen direkten Vor- bzw. Nachfolger der Stelle s in c dar. Je nachdem, ob in a und b nun noch genügend Knoten vorhanden sind, um zwei Seiten zu füllen, findet entweder ein Ausgleich zwischen den beiden Seiten statt (Zeilen 298-308 und 333-345), oder die Seiten werden zu einer Seite zusammengefaßt (Zeilen 312-319 und 349-356). Die genaue Verbalisierung dieser im Großen einsichtigen, im Detail aber unübersichtlichen Sache schenke ich mir und Ihnen.

Zurück zum Hauptblock von delete_data. Nach dem Aufruf von search und der hier erfolgten Mißhandlungen unseres B-Baumes, besteht noch die Möglichkeit, daß ein Unterlauf in unserem Wurzelknoten aufgetreten ist. Wie Sie den bisherigen Beispielen sicherlich entnommen haben, ist dies bis zu einem gewissen Grad erlaubt:

Entgegen den Definitionen für eine beliebige Seite, muß sich lediglich ein Element im Wurzelknoten befinden.

Wenn es aber auch an diesem einen Element mangelt (Zeile 459), muß etwas unternommen werden:

A: Bei leerem linken Nachfolger ist der Baum völlig entleert und das ist unserem Programm durch setzen der Variable tree auf leer mitzuteilen.

B: Bei einem linken Nachfolger, ist dieser zu unserer Wurzelseite zu machen und die ehemalige Wurzel ist als gelöscht zu kenn- zeichnen (Setzen des Archivierungsflag). Beachten Sie dabei bitte auch, daß die beiden Datensätze q und tree auch physikalisch ausgetauscht werden (Zeilen 469-472).

Abschließend sind noch die Datenseiten des gelöschten Schlüssels aus der Datenbank zu entfernen. Zu diesem Zwecke wird in einer WHILE Schleife die del_list durchlaufen, wobei die entsprechenden Archivierungsflags auf false gesetzt werden.

search_ptr

search_ptr stellt nun die dritte und letzte Variante des Suchens in B-Bäumen dar.

Sie tut weiter nichts, als die Random-Access-Adresse eines durch key bezeichneten Datenbankeintrages (nicht Index) zu ermitteln. Der prinzipielle Aufbau ist gleich denen bei insert_data und delete_data, nur das keine so verwegenen Operationen auf der ermittelten Seite ausgeführt werden.

search_first und search_next

search_first sucht den ersten Datensatz mit bezeichnetem Schlüssel key in der Datenbank. Hierzu wird die Funktion search_ptr benutzt. Der Erfolg oder Mißerfolg wird über einen bool'schen Funktionsreturn kundgetan. Weiterhin ist die globale Variable next_list zu erwähnen, die das Auffinden eines dem ersten Datensatz nachfolgendem Element mit search_next erst ermöglicht. Durch wiederholten Aufruf von search_next kann so die gesamte Elementnachfolgerliste durch-schritten werden.

print_tree

Die Prozedur print_tree stellt eine Variante des Präorderdurchlaufs durch eine B-Baumstruktur dar. Zunächst werden dabei sämtliche Schlüsselelemente ausgegeben und hierauffolgend die Liste sämtlicher Nachfolger durchlaufen. Nebenbei wird dabei auch noch, je Element, die Elementnachfolgerliste in der Datenbank durchlaufen. Zusammen mit einer Baumtiefevariable, tiefe, die bei jedem rekursivem Abstieg inkrementiert wird und mit den Schlüsselelementen ausgegeben wird, ergeben sich dabei recht anschauliche Baumdarstellungen.

Spielt man ein wenig mit den Baumordnungen herum, so kann man mit print_tree Informationen darüber gewinnen, wie schnell B-Bäume in Abhängigkeit von ihrer Ordnung wachsen. In Abbildung 6c erkennen Sie, daß die Baumtiefe, schon bei leicht erhöhter Ordnung sehr stark abnimmt. Schlußfolgerungen, die man dadurch über die optimalen Ordnung gewinnen kann, sind aber sehr von der Größe der Schlüssel und der Organisation auf Datenträgern abhängig. Sie können aber in den meisten Fällen davon ausgehen, daß eine Seite immer dann recht effektiv geladen wird, wenn das gesamte Seitenformat ungefähr der Verarbeitungsgröße auf dem benutzten Massenspeicher entspricht.

Abbildung 6c:

Baumtiefe im Zusammenhang mit dem Grad des Baumes (30 Baumelemente)

Grad 1:               Grad 2:
1: 43 (28/91)         1: 43 (28/91)
2: 23 (66)            2: 9 (3) 23 (66) 28 (5/98/71)
3: 8 (84) 15 (99)     3: 7 (23) 8 (84)
4: 7 (23)             3: 15 (99) 20 (93/23)
4: 9 (3)              3: 24 (76) 27 (80/74)
4: 20 (93/23)         3: 29 (1) 32 (18)
3: 28 (5/98/71)       2: 50 (12) 60 (87) 64 (78)
4: 24 (76) 27 (80/74) 3: 45 (66) 46 (70) 48 (3)
4: 29 (1) 32 (18)     3: 61 (18) 63 (14)
2: 61 (18)            3: 66 (6) 73 (2) 80 (6)
3: 48 (3) 51 (98)
4: 45 (66) 46 (70)    Grad 4:
4: 50 (12)            1: 24 (76) 45 (66) 63 (14)
4: 55 (90) 60 (87)    2: 7 (23) 8 (84) 9 (3) 15 (99) 20 (93/23) 23 (66)
3: 66 (6)             2: 27 (80/74) 28 (5/98/71) 29 (1) 32 (18) 43 (28/91)
4: 63 (14) 64 (78)    2: 46 (70) 48 (3) 50 (12) 51 (98) 55 (90) 60 (87) 61 (18)
4: 73 (2) 80 (6)      2: 64 (78) 66 (6) 73 (2) 80 (6)

Beispiel: Unser ST hat als Grundgröße für Dateien das Cluster (1 kByte). Unser Variablenformat (Schlüssel in integer) ergibt sich zu 8+8*nn Byte (kleiner Überschlag der Typensumme des RECORD page_type). Hieraus würde sich eine 'günstige' Ordnung von etwa 63 ergeben.

Testumgebung

Zur Testumgebung (Listing 6c) ist nicht viel zu sagen. Über einen trivialen Operationsaufruf hinaus, ist nur die Routine zur Erzeugung einer 'gewissen' Anzahl von Zufallseinträgen zu nennen, die einem beim Testen viel Tipperei abnimmt.

Packen

Den Packalgorithmus, zur Entfernung der leeren Datensätze, habe ich in einem gesonderten Programm untergebracht (Listing 6d).

Um zu sehen, wie nötig man das Packen mal wieder gehabt hat, besitzt dieses Programm zunächst zwei kleine Funktionen, die durch einfachen Durchlauf der jeweiligen Datei den prozentualen Anteil der gefüllten Datensätze ermittelt (Zeilen 23-43 für die Indexdatei, Zeilen 45-65 für die Datenbank).

Das eigentliche Packen geschieht nun in mehreren Phasen.

A: abstand_besorgen

Zunächst werden die Anzahlen der aufeinanderfolgenden gefüllten und leeren Datensätze der beiden Dateien in den Puffern p_index und p_data untergebracht. Dabei treffen wir die Konvention, daß immer mit einer Sequenz von gefüllten Datensätzen begonnen wird. In den ungeraden Indizes der Puffer haben wir hiernach die Längen der noch gültigen Sequenzen; in den geraden Indizes die Längen der zu entfernenden Sequenzen.

B: abstand_kumulieren

Durch das Rausschmeißen der leeren Datensätze, ändern sich die meisten (fast alle) der page_ptr und data_ptr in den verbleibenden Datensätzen. Um die neuen Indizes dieser Datensätze mit möglichst geringem Aufwand berechnen zu können, addieren wir die Anzahl der belegt/unbelegt Sequenzen, in den beiden Puffern, auf.

Und zwar auf vollgende Weise:

Von links beginnend, berechnen wir in den ungeraden Indizes die Gesamtanzahl aller (belegt und unbelegt) vorstehenden Sequenzen. In den geraden Indizes berechnen wir nur die Gesamtanzahl der vorstehenden unbelegten Sequenzen.

Mit new_index (bzw. new_data) können wir danach sehr leicht die neuen Indizes berechnen, indem wir die ungeraden Pufferstellen bis zur Überschreitung der alten Indexzahl entlangwandern. Der neue Wert ergibt sich dann sehr leicht durch Differenzbildung mit dem vorstehenden geraden ARRAY-Index.

C: index_packen und data_packen

In den eigentlichen Packroutinen, sind nun nur noch, unter Auswechslung sämtlicher alter Indizes durch die Neuen, die gültigen Datensätze in eine temporäre Datei zu kopieren. Hiernach erfolgt nur noch die Umbenennung der Temporären, in die alte Dateibezeichnung.

Vorausschau

So das wär's !!! Die Bäume sind tod. In der nächsten Folge von Algorithmen & Datenstrukturen, werden Sie Hashing-Verfahren kennenlernen, die mitunter auch recht hilfreich bei der DV sind. Sie können aufatmen. Die Listings werden dabei nämlich merklich kürzer und durchsichtiger. Bis dann,

Listings zu diesem Artikel