Nachdem wir in der letzten Ausgabe über die Hardware des MC 68881 Arithmetikprozessors und seinen Einbau in den ATARI ST gesprochen haben, wollen wir uns diesmal etwas mit der Softwareunterstützung beschäftigen. Denn ohne Software nützt auch der schnellste und schönste Coprozessor nichts, erst zusammen bilden sie eine leitungsfähige Einheit.
Als stolzer Käufer einer FPU (Floating Point Unit), auch Arithmetik-Coprozessor genannt, stellt sich einem zuerst die Frage, ob der Prozessor, den man in seinen Rechner eingebaut hat, überhaupt richtig arbeitet. Dazu werden vom Hersteller Testprogramme mitgeliefert, die die Speicheradresse $FFFA40 abfragen. Diese Adresse ist die von ATARI herausgegebene Basisadresse für die FPU, ab der 128 Byte reserviert sind. Ist keine FPU vorhanden bzw. ein Fehler beim Einbau passiert, so wird ein Buserror erzeugt, was daher rührt, daß beim ST dieser Adressbereich für eine Ein- bzw. Ausgabe auf externe Geräte vorgesehen ist. Ist ein solches Gerät nicht vorhanden oder es kann nicht angesprochen werden, wird logischerweise ein Buserror erzeugt. Damit sind wir an einem Hauptmerkmal der ST-FPU angelangt, sie wird nämlich als externes Gerät verwaltet.
Ist dagegen eine FPU eingebaut und funktioniert richtig, wird jener Buserror, insoweit er sich auf sie bezieht, von ihr abgefangen. Wie solche Testroutinen aussehen, kann man anhand der Listings 1 (Megamax C) und 2 (Omikron Basic) sehen.
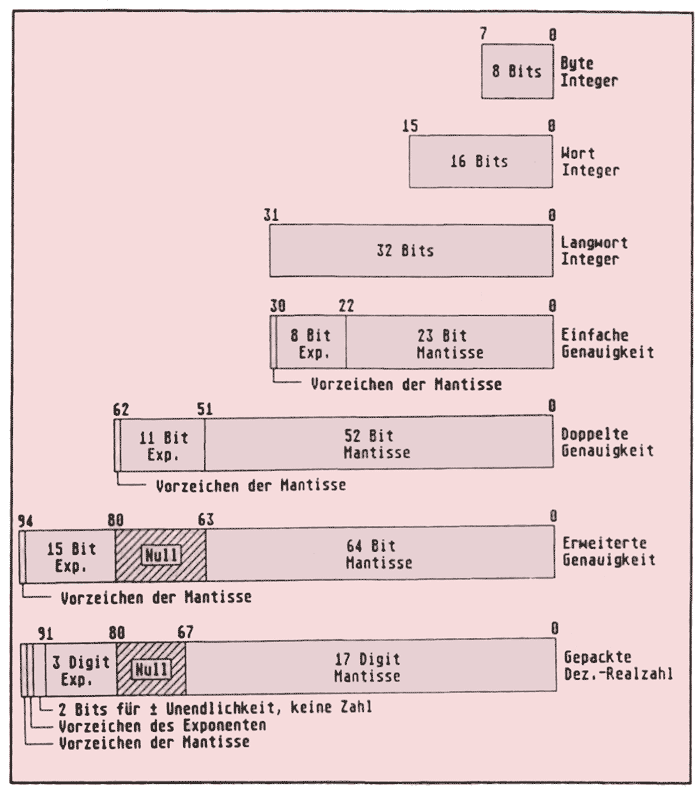 Bild 1: Die Datenformate des MC 68881
Bild 1: Die Datenformate des MC 68881
Was kann der Matheproz?
Wie man bereits in der letzten Ausgabe lesen konnte, unterstützt der MC 68881 die Grundrechenarten und alle wichtigen trigonometrischen Funktionen. Er besitzt eine Vielzahl an Zahlenformaten nach dem IEEE-Standard, die man zuerst einmal der folgenden Tabelle entnehmen kann, bevor wir näher darauf eingehen:
B
Byte Integer (8 Bit)
W
Wort Integer (16 Bit)
L
Langwort Integer (32 Bit)
S
Realzahl mit einfacher Genauigkeit (32 Bit)
D
Realzahl mit doppelter Genauigkeit (64 Bit)
X
Realzahl mit erweiterter Genauigkeit (80 Bit)
P
Gepackter Dezimal-Realzahlen-String (BCD) (80 Bit)
Zu den Integer-Formaten gibt es nur insoweit etwas besonders zu bemerken, daß sie, sobald sie in Verbindung mit Realzahlen benutzt werden, automatisch in Realzahlen mit erweiterter Genauigkeit (Extended) umgewandelt werden. Ansonsten bleibt alles wie gewohnt.
Bei den Realzahlen tut sich dagegen einiges, wie man ja schon der Tabelle entnehmen konnte. Zunächst folgt wieder eine kleine Tabelle mit der Einteilung der Längen der verschiedenen Genauigkeiten in Mantisse und Exponent. Generell kommt hier ein Bit für das Vorzeichen der Mantisse hinzu.
| Datenformat |
Exponenten |
Mantissen |
Vorzeichen |
| Bits |
Bits |
Bit |
|
| Einfach |
8 |
23 |
1 |
| Doppelt |
11 |
52 |
1 |
| Erweitert |
15 |
64 |
1 |
Die jeweilige Verteilung der Bits auf Mantisse, Exponent und Vorzeichen kann man nochmal anschaulich Bild 1 entnehmen. Hierbei fällt auf, daß das erweiterte Format 16 Bit ungenutzt läßt. Diese sind für künftige Erweiterungen noch unbenutzt. Man nutzt dieses erweiterte Format hauptsächlich für temporäre Variablen, Zwischenwerte oder einfach um die größtmöglichste Genauigkeit zu erreichen.
Als letzter Formattyp wird ein sogenannter gepackter Dezimal-Realzahlen-String zur Verfügung gestellt. Auffallend ist hier, daß es sich um keine Zahl im eigentlichen Sinne, sondern um einen String handelt. Dieser ist in einen drei Digit Exponenten und eine 17 Digit Mantisse unterteilt. Sowohl Exponent als auch Mantisse haben zusätzlich je ein eigenes Vorzeichen-Bit. Zwei Bits werden u. a. für ± Unendlichkeit, Null oder dann genutzt, wenn keine Zahl vorliegt. Ähnlich wie beim Extended-Format bleiben auch hier einige Bits ohne Bedeutung, da sie für künftige Erweiterungen bestimmt sind. Der komplette String hat eine Länge von 96 Bits (drei Langwörter).
Beliebige Zahlenkonvertierung
Prinzipiell werden alle sechs Datenformate vom MC 68881 in das Extended-Format (das Siebte ist ja das Extended-Format) zu weiteren internen Berechnungen umgewandelt, also auch das letztgenannte Stringformat.
Folglich kann dies auch zur Konvertierung in ein anderes der sechs Zahlenformate benutzt werden. Will man also zum Beispiel von einfacher auf doppelte Genauigkeit umrechnen, wird die Zahl mit der einfachen Genauigkeit zuerst in das Extended-Format zur internen Berechnung und dann in die doppelte Genauigkeit gewandelt.
Tabelle 1: Rechenbereiche der Realzahl-Formate
| Genauigkeit |
+ Rechenbereich |
- Rechenbereich |
| einfach |
3,4 * 1038 |
1,2 * 10-38 |
| doppelt |
18 * 10307 |
2,2 * 10-308 |
| erweitert |
6 * 104931 |
8 * 10-4933 |
Was unterstützt was?
Eine Reihe von Softwareherstellern haben bereits Anpassungen an den Arithmetikprozessor vorgenommen, weitere werden demnächst fertig. Als fertige Programme existieren bis jetzt nur Programmiersprachen. Doch da die Quelltexte fertiger Programme nur mit der 68881-Version des jeweiligen Compilers neu copiliert zu werden brauchen, dürften auch seine Vielzahl von Anwenderprogrammen, die bisher durch enorme Berechnungen gebremst werden, auf den Markt kommen. Allerdings müssen dann Versionen sowohl mit als auch ohne 68881 Unterstützung existieren, da man ansonsten den anfangs beschriebenen Bus-error erhält.
Einige Programmiersprachen benötigen zuerst einmal Zeit für die Umrechnung auf ein dem Coprozessor verständliches Zahlenformat. Dazu zählen u. a. Lattice C und alle Digital Research Produkte aus dem ATARI Entwicklungspaket (Assembler, C). Dadurch wird der Effekt der Arithmetik-Unterstützung natürlich geschmälert, aber es rentiert sich trotzdem einen Coprozessor einzubauen.
Fertige Anpassungen, die ohne diese Zahlenkonvertierung auskommen, sind in alphabetischer Reihenfolge folgende Produkte:
- GFA BASIC Interpreter / Compiler
- Lattice C Compiler
- Megamax C Compiler
- OMIKRON BASIC Compiler
GFA BASIC
Gehen wir der Reihe nach vor. GFA Systemtechnik bietet sowohl einen Basic-lnterpreter als auch einen Compiler in einem Paket unter dem Namen GFA BASIC 68881 an. Es handelt sich um eine dem Arithmetikprozessor angepaßte Spezialversion der normalen Version 2.0. Dadurch wird die Genauigkeit von knapp elf Stellen auf knapp 16 Stellen (doppelte Genauigkeit) erhöht. Neben einigen kleinen Verbesserungen sind auch neue Befehle hinzugekommen, die die Arbeit mit dem Coprozessor vereinfachen, da sie die wichtigsten mathematischen Befehle des Prozessors darstellen.
Der Interpreter benötigt im Gegensatz zum Compiler unbedingt den Coprozessor. Es ist also möglich auf einem „normalen“ Rechner die Programme zu schreiben und zu compilieren. Allerdings laufen sie logischerweise nur auf einem ST mit Arithmetikprozessor. Dies ist wohl nur bedingt ein Vorteil, denn man kann nur theoretisch programmieren, ohne Programmteile austesten zu können.
Geliefert werden zwei verschiedene Versionen des GFA BASIC 68881 und zwar eine für Short- ($FFFA40) und eine für Long-adressierte ($EFFF80) MC 68881 Prozessoren. Für den, von uns verwendeten, Coprozessor von Lischka Datentechnik und für alle, die nach der ATARI-Adresse arbeiten, ist die Short-Adressierung notwendig. Der Preis für GFA BASIC 68881 Interpreter und Compiler beträgt zusammen DM 349,-.
a=TIMER
FOR x%=1 TO 100
FOR y%=-98 TO 99
w=ATN(y%/*%)
r=LOG(SQR(x%*x%+y%*y%))
h=0.5*(SIN(2*w+r*10))
IF h>0 THEN
PLOT 120-x%,200*y%
PLOT 119+x%,200-y%
ENDIF
NEXT y%
NEXT x%
PRINT (TIMER-a)/200
Listing 3: GFA BASIC Benchmark.
Lattice C Compiler
Für diesen C Compiler wird eine Anpassung direkt von Lischka Datentechnik mitgeliefert. Logischerweise ist es für einen C Compiler nur eine zusätzliche Library. Da Lattice C normalerweise in doppelter Genauigkeit rechnet, wandelt der Prozessor dieses zuvor in das Extended-Format um, was die ganze Sache leider verlangsamt.
Megamax C Compiler
Es ist eine Minimal-Anpassung im Lieferumfang der Lischka Version enthalten. Wem diese Version nicht genügt, kann bei Application Systems /// Heidelberg eine Profiversion erwerben. Bei Megamax C müssen einfach die Libraries „trig.o“ und „fmath.o“ ausgetauscht werden. Hier gilt dasselbe wie für den Lattice C Compiler. Der Megamax C rechnet normalerweise in doppelter Genauigkeit, und der Prozessor muß somit vorerst in die erweiterte Genauigkeit konvertieren. Die Profiversion wird auf einer Diskette zusammen mit der Mathematik-Library „Giga Joe“ für DM 80,- geliefert. Wer allerdings schon im Besitz des Giga Joes ist, kann die Profi-Anpassung an den Arithmetik-Prozessor gegen einen Rabatt von DM 40,- eintauschen. Dies gilt selbstverständlich nur für registrierte Kunden.
#include <osbind.h>
#include <stdio.h>
#define fp881 0xfa40 /* Floating point Basisadresse (short) */
#define response 8xfa40 /* Response-Register (nur lesen) Antwort */
#define command 0xfa4a /* Command CIR (nur schreiben) */
#define Operand 0xfa50 /* Operand CIR llesen/schreiben) */
#define fmovl_0 0x7400
#define MY_100 0x5C34
#define TRUE 1
#define FAL5E 0
#define HUNDRED 100
extern rx(), result(), find_68881();
int _fpu881;
main()
{
find_68881();
if (_fpu881)
printf("Der Matheprozessor Ist da\n");
else
printf('Bin ohne Matheprozessor\n');
Cconin();
}
asm
{
rx: move.l A0,(A7)+ ; A0 sichern
lea result(PC),A0
move.w #TRUE,(A0) ; Adressfehlerflag setzen
move.l -(A7),A0
addq #8,A7 ; Stack korrigieren
rte
result: dc.w 0
}
find_68881()
{
_fpu881 = FALSE;
if (!bus_error(fp881))
{
if (test_fpu())
{
_fpu881 = TRUE;
}
}
}
bus_error(adress)
long adress;
{
long oldbus;
oldbus = Setexc(2, rx):
asm
{
lea result(PC),A0
move.w #FALSE,(A0) ; Clr Adress Fehler
move.w #0,command ; mache Adress Error
}
Setexc(2, oldbus);
asm
{
move.w result(PC),D0 ; Return Adress Fehler
}
}
test_fpu()
{
double result = 0.0:
asm
{
move.w #MY_100,command
ffw1: cmpi.H #0x8980,response ; ist '881' busy ?
beq.s ffw1 ; warten f
move.w #fmovl_0,command
ffpiw3: cmpi.w 00x8900,response ; ist '881' busy ?
beq.s ffpiw3 ; warten, bis '881' fertig ist
move.l operand,result(A6) ; Operanden holen
move.l operand,result+4(A6)
}
return (result == HUNDRED);
}
Listing 1: Testprogramm in Megamax C.
OMIKRON BASIC
Für dieses Basic wird ein Compiler mit 68881-Unterstützung angeboten. Durch ihn erhöht sich die Rechengenauigkeit des OMIKRON BASICs auf ca. 19 Stellen (Extended-Format). Es wird ähnlich wie bei den C-Compilern eine zusätzliche Library mitgeliefert. Der Preis beträgt DM 229,-. Ist man bereits stolzer Besitzer eines OMIKRON BASIC Compilers, kann man die 68881-Version gegen DM 60,-Aufpreis eintauschen.
100 ON ERROR GOTO 140
110 A= WPEEK($FFFA40)
120 ON ERROR GOTO 8
130 GOTO 150
140 PRINT "FPU nicht vorhanden": RESUME 120
150 '
Listing 2: Testprogramm in OMIKRON BASIC.
Benchmarks
Nun kommen wir zu den beliebten Benchmark-Tests. Diese Benchmarks sind aber keine Benchmarks im herkömmlichen Sinne. Wir haben nicht genau dasselbe Listing für alle Programmiersprachen genommen (ist ja auch gar nicht möglich!), sondern haben versucht möglichst optimal, d. h. geschwindigkeitsoptimiert, zu programmieren. Es ist wohl sinnvoller aufzuzeigen wie man dasselbe Ziel in der jeweiligen Sprache am besten erreichen kann. Natürlich gibt es sicherlich noch schnellere Lösungen, man denke nur an den Inline-Assembler von Megamax C, doch dies hätte dann doch zu weit geführt. Bei OMIKRON BASIC und Megamax C wurden eigen definierte Routinen zum Setzen eines Punktes auf dem Bildschirm benutzt, da sich herausgestellt hat, daß die meiste Zeit durch die VDI-Routine v_pline verloren geht. Deswegen kann man sicherlich auch noch die GFA BASIC-Routine um einiges beschleunigen.
Man kann auf diesen Seiten jeweils ein Listing in GFA BASIC, OMIKRON BASIC und Megamax C finden. Die Benchmarks zu den Sprachen, geben noch Zeiten von anderen Lösungsversionen und unterschiedlichen Bedingungen an.
#include <math.h>
#include <osbind.h>
#include <stdio.h>
#include <gemdefs.h>
long *ptr;
char *screen;
main()
{
appl_init();
graf_mouse(M_OFF, 0L);
execute();
graf_mouse(M_ON, 0L);
appl_exit();
}
gettime()
{
*ptr = *(long #)0x462;
}
execute()
{
register int xd,yd;
long t,t2;
double x,y,w,h;
ptr = &t;
Supexec(gettime);
screen = (char*) Physbase();
cls();
for (xd=1; xd<=100; xd++)
{
x = (double)xd;
for (yd = -100; yd<=100; yd++)
{
y = (double)yd;
m = atan(y/*);
h = sin(w+w+log(sqrt(x*x+y*y))*10);
if (h >= 0.0)
{
Plot (270-xd,200+yd):
Plot (269+xd,200-yd);
}
}
}
ptr = &t2;
Supexec(gettime);
printf("Took %0.2f seconds\n", (double)(t2-t)/(Getrez() == 2 ? 70 : 60));
Cconin();
}
Plot(x,y)
register unsigned int x,y;
{
register char *s;
s = screen+y*80+(x>>3);
*s |= 128>>(x&7);
}
cls()
{
register long *s;
register long i;
s = (long*) screen;
for (i=0; i<8000: i++)
*s++ = 0L;
}
Listing 4: Megamax C Benchmark.
Scr=FN Logbase:Fpu_Errors_Off
A= TIMER
FOR X=1 TO 100
FOR Y=-98 TO 99
W!= ARCTAN(Y/X)
R!= LN( SQR(X*X+Y*Y))
M!= 5*SIN(W!*2+R!*10)
IF H!>0 THEH
Draw_Sw(120-X,200+Y)
Draw_Sw(119*X,280-Y)
ENDIF
NEXT Y
NEXT X
PRINT( TIMER -A)/200
A$= INPUTS(1): ENO
OEF PROC Fpu_Errors_Off: RETURN
OEF PROC Draw_Sw(X,Y); BIT ( NOT X AND 7,Scr+X SHR 3+Y*80)=1: RETURN
DEF FN Logbase: LOCAL R: XBIOS (R,3): RETURN R
Fpu_Errors_Off
END
DEF PROC Fpu_Errors_Off: RETURN
Listing 5: OMIKRON BASIC Benchmark.
Fazit
Bei einem Preis von über DM 700,-sollte man sich schon überlegen, ob man einen Arithmetik-Coprozessor braucht, zumal noch die Kosten für die jeweilige Programmiersprache bzw. Programmversion hinzukommen. Er ist wohl hauptsächlich in naturwissenschaftlichen und zeitkritischen Bereichen sinnvoll. Allerdings, wenn die ersten Anwenderprogramme unterstützt werden, kann er schon eine ganze Menge an Wartezeit bei Berechnungen sparen helfen.
HE
Benchmarks in s:
GFA BASIC Interpreter 131.97
GFA BASIC Compiler 97.10
GFA BASIC 881 Interpreter 55.52
GFA BASIC 881 Compiler 24.67
Megamax C Compiler
mit Mathe-Library (Giga Joe) 296.00
Megamax C Compiler 881
mit eigener Punkt-Routine 22.85
OMIKRON BASIC Interpreter 97.41
OMIKRON BASIC Compiler 76.98
OMIKRON BASIC 881 Compiler * 26.93
OMIKRON BASIC 881 Compiler mit DEFPROC-Definition 14.33