Den Einsteiger in C lehren sie sehr schnell das Fürchten: Die dynamischen Felder, derer sich die bereits an anderer Stelle behandelten verketteten Listen ausgiebig bedienen. Für den erfahrenen C-Programmierer sein täglich Brot, sind sie doch für den Neuling oftmals das Buch mit den berühmten sieben Siegeln: die Pointer. GEM macht von diesen (zumindest für Einsteiger) ominösen Gesellen regen Gebrauch und schreckt so manchen gutwilligen Anfänger ab.
Dabei ist das alles noch nicht einmal übertrieben dargestellt: Viele Studenten technischer Studiengänge erleben eher zwangsweise den Einstieg in die Programmierung in C. Meiner unerheblichen Meinung nach ein denkbar schlechter Einstiegspunkt. Im Gegensatz zu Pascal, einer als reines Lehrmittel konzipierten Sprache, oder FORTRAN, einer Sprache zur EDV-gerechten Formulierung technischer Probleme und Formeln (FORmula TRANslation), ist und bleibt C eine Sprache von Programmierern für Programmierer. Und die verlangt einiges Wissen über die Zusammenhänge in der Variablenverwaltung und ein gehöriges Stück Selbstdisziplin des Programmierers. Aber es gibt kaum eine zweite Sprache, mit der der Umgang mit dem Rechner so flexibel und, wenn nötig, auch sehr systemnah gestaltet werden kann. Und wer es kann, kann sehr elegant und trickreich programmieren ...
Die Variable in der theoretischen Betrachtung
Nach so vielen allgemeinen Worten wenden wir uns endlich dem eigentlichen Thema zu. Egal, wie wir unsere Daten im Speicher organisieren, drei Dinge sind immer vorhanden: eine Adresse und der dazugehörige Inhalt (hier ,Wert‘ genannt) - ohne Adresse weiß niemand, wo der Wert steht, existiert aber eine Adresse, existiert auch automatisch ein Wert. Um die Größe des Wertes ab einer Adresse bestimmen zu können, bedarf es dazu noch einer Angabe, wie weit ab der Adresse gelesen werden soll - der Länge. Adresse, Länge, Wert - jede Variable wird durch diese drei Parameter bestimmt.
Der Einstieg in die Programmierung
Jetzt geht es in die Vollen. Werfen wir dazu doch mal einen Blick auf Bild 1. Die Legende zeigt zwei Arten von Variablen und die bereits erwähnte Startadresse. Die erste Variablenart wird vom Compiler fest im Programm eingebaut, mit fester Länge und fester Adresse. Um das deutlich zu zeigen, befindet sich der Speicherbereich der Variablen in einer "festen" Schraffur. Die zweite Art der Variablen ist wirklich variabel. Sie hat keine feste Adresse, ihr Wert ist zunächst auch nicht bekannt, und das Beste an diesen Variablen: direkt, nachdem das Programm geladen wurde und noch keine einzige Anweisung ausgeführt ist, existieren sie überhaupt noch nicht! Was aber existiert, ist eine Art Hilfsvariable: der Pointer.
Das erste Programm - und gleich dynamisch!
Rechts neben der Legende ist noch ein zweiter, eher unscheinbarer Kasten. In ihm steht das zu dem Bild gehörende C-Programm. Der Einfachheit halber benutze ich hierin nur vier Byte lange ganze Zahlen, die sog. long-Integers. Auf den neueren Rechnern von ATARI hat eine Speicheradresse eine Länge von 32 Bit, also 4 Byte. Das wird nicht in alle Ewigkeit so gehen, schon jetzt existieren 64-Bit-Architekturen (z.B. der ATARI ,Jaguar‘ oder die DOS-Rechner mit Pentium-Prozessor, also mit einem Intel 80586), aber das nur zur Warnung. Hätten einige der Programmierer das bedacht und sich in eingangs erwähnter Selbstdisziplin geübt, gäbe es etliche TT - und Falcon-taugliche Programme mehr - aber das nur am Rande. Aufgrund der einigermaßen geschickten Wahl des Variablentyps gestaltet sich die Zeichnung als recht einfach. Aber was passiert in diesem Programm?
Der Compiler wird zunächst darüber informiert, welche Datenspeicher er aufzubauen hat. Diese werden im Maschinenprogramm fest verankert. Da wäre
long *PointerName, ...
Damit wird dem Compiler mitgeteilt, daß er eine Pointer-Variable PointerName einrichten soll, die später die Startadresse des Datenfeldes vom Typ long mit dem Namen *PointerName enthalten soll.
Der zweite Eintrag
... VarName;
erzeugt eine einzelne long-Integer mit dem Namen VarName, der sofort ein Wert zugewiesen werden kann.
Betrachten wir die nächste Zeile: Hier wird mit der C-Funktion calloc() Speicherplatz für vier Variablen der Größe einer long angefordert und der Pointervariablen PointerName zugewiesen. Erst ab diesem Moment existiert das Datenfeld *PointerName.
Die vier Elemente von i:PointerName werden eigentlich mit *PointerName, *( PointerName+1), *(PointerName+2) und *(PointerName+3) angesprochen. Da aber diese Schreibweise recht umständlich ist, kann das Datenfeld statt mit *(PointerName+i) auch mit dem viel einfacheren PointerName[i] angesprochen werden, beide Schreibweisen sind jederzeit austauschbar. Wie nützlich dieses Verhalten von C ist, wird etwas später noch deutlicher.
In den folgenden vier Zeilen werden denElementen des Datenfeldes *PointerName willkürliche Werte übergeben, die auch im Bild zu sehen sind. In der letzten Zeile wird der Unterschied zu einer Einzelvariablen deutlich, denn VarName kann nur einen einzigen Wert aufnehmen.
Von der Liste zur Matrix
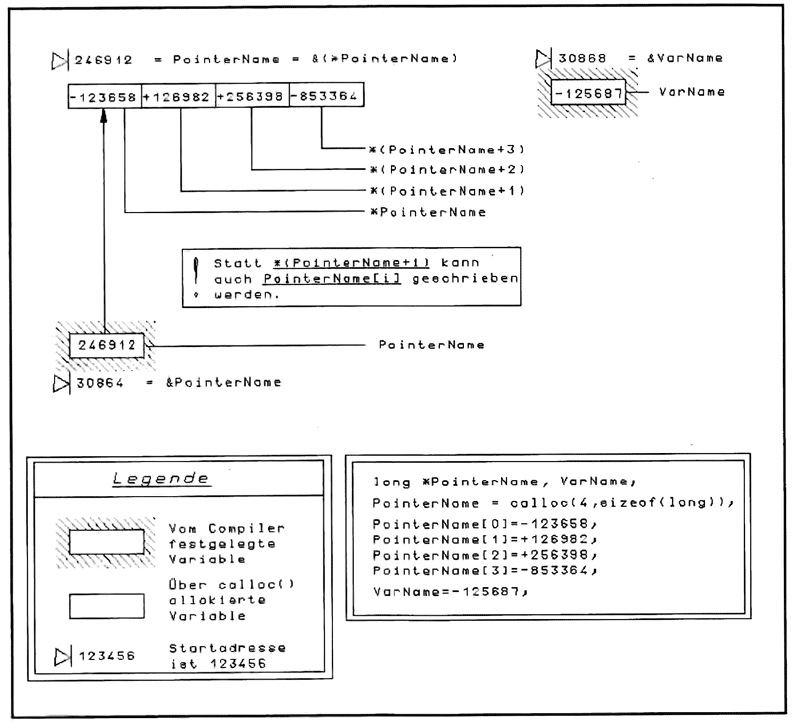 Bild 1: Die beiden grundsätzlichen Variablenarten
Bild 1: Die beiden grundsätzlichen Variablenarten
Das Datenfeld *PointerName ist seinem Aufbau nach eine Liste, deshalb wird es auch so genannt. In der Mathematik heißt eine Liste auch Vektor, und eine Tabelle wird dort auch Matrix genannt. Der Programmierer kennt für beide außerdem noch die Begriffe indizierte Variable oder einfach: Array (engl, für Feld, Bereich).
Die Liste ist ein eindimensionales Array, die Tabelle ein zweidimensionales, und für jeden weiteren Index wird die Anzahl der Dimensionen um eins erhöht. Statt mit den Dimensionen zu spielen, kann der Begriff des Arrays auch mit einer Ordnungszahl erweitert werden, so wäre dann ein Vektor ein Array 1. Ordnung, eine Matrix ein Array 2. Ordnung usw. In Bild 2 sind die Zusammenhänge zwischen Vektor, Matrix und dreidimensionalem Array recht deutlich zu erkennen: Der Anfang ist immer ein Vektor, in Bild 2 dick umrandet und mit einer Kreuzschraffur versehen. Dieser Vektor entstand auf die weiter oben beschriebene und in Bild 1 dargestellte Art und Weise. Was wäre denn, wenn jedes Element des Vektors in Bild 2 wieder seinerseits zu einem Vektor erweitert würde? Das Ergebnis ist etwas dünner umrahmt und mit einer einfachen Schraffur versehen - es entsteht eine Tabelle bzw. eine Matrix bzw. ein zweidimensionales Array bzw. ein Array 2. Ordnung.
 Bild 2: Der Aufbau mehrdimensionaler Felder
Bild 2: Der Aufbau mehrdimensionaler Felder
Der nächsten Schritt könnte die Überschrift tragen: Von der Matrix zum Quader, denn wird jedes Element der eben erzeugten Matrix wiederum zu einem Vektor erweitert, entsteht ein solcher. In Bild 2 ist der Quader dünn gezeichnet.
Nun sollen die Elemente ja noch angesprochen werden können. Das geschieht mit Hilfe der Indizes i, j, k. Mit dem Index i kann der Vektor angesprochen werden, so wie in Bild 1 geschehen, mit den Indizes i, j wird die Tabelle erfaßt, und die Indizes i, j, k gelten für das Array 3. Ordnung.
Manchmal ist es nötig zu wissen, welcher Index sich am schnellsten bei der Verwaltung innerhalb des Programms ändert, welche Elemente also direkt hintereinander liegen. Aus dem Aufbau mehrdimensionaler Felder aus einem Vektor erklärt es sich deshalb schon fast von selbst, daß immer der letzte Index am schnellsten durchgezählt wird.
/*
Listing 1
für Turbo C 2.0
Autor: T.W. Müller
(C) by Maxon Computer GmbH, 1994
*/
#include <stdio.h>
#define Nmax 3
main()
{
int Vektor[] = { 1, 2,3};
int i;
for (i=0;i<Nmax;i++)
printf("\nVektor[%d] = %d\n",i,Vektor[i]);
getchar();
/* Sonst meckert TC.PRG nach Programmende. */
return 0;
}
Listing 1
Von der Flexibilität
In Listing 1 ist ein kleines Programm abgedruckt, das einen Vektor mit 3 Elementen fest dimensioniert und gleichzeitig mit Werten vorbesetzt. Das Programm in Listing 2 macht etwas ähnliches, aber da zu Anfang der Vektor gar nicht existiert, müssen die Werte nach der dynamischen Dimensionierung zugewiesen werden. Hier zeigt sich der Vorteil der austauschbaren Schreibweisen.
In den Listings 3 und 4 wiederholt sich das Spielchen, nur mit Matrizen. Wer sich inzwischen gefragt hat, wie denn der Compiler bei der dynamischen Dimensionierung unterscheiden kann, wieviele Indizes ihn erwarten, findet hier die Antwort auf seine Frage: Die Anzahl der Referenzierungszeichen (also der Sternchen ,*‘) vor dem Pointer-Namen sagt es ihm. Anmerkung: Der Ausdruck ,Referenzierung‘ bedeutet, daß statt der Variablen ihre Adresse angesprochen wird. Das ist sehr pauschal ausgedrückt, aber an dieser Stelle vollends ausreichend, wenn man sich merkt, daß eine Referenz(ierung) irgend etwas mit der Variablenadresse zu tun hat. Zunächst wird, wie gehabt, eine Liste dimensioniert, die so viele Elemente hat wie die Matrix Zeilen. Der Unterschied besteht nun darin, daß jedes Element dieser Liste auch nur wieder ein Pointer auf eine weitere Liste ist. Also muß im zweiten Schritt für jeden dieser Pointer nochmals Speicher angefordert werden. Hat alles fehlerfrei funktioniert, ist die Matrix fertig.
Bisher war immer nur von einer Matrix die Rede, genauer gesagt, von einer Rechteckmatrix. Wer sich schon einmal mit dem Lösen von Gleichungssystemen beschäftigt hat, kennt den Begriff der Dreiecksmatrix. Eine solche Matrix benötigt bei i=1 nur ein Element, bei i=2 zwei Elemente und das so weiter, bis bei i=N N Elemente benötigt werden. Natürlich kann eine solche Matrix ohne Probleme in eine NxN-Rechteck-Matrix gelegt werden, allerdings wird die Hälfte des Speicherplatzes nie genutzt. Natürlich ist der Aufbau einer Dreiecksmatrix nicht die einzige Möglichkeit, die Flexibilität dieses Verfahrens zu nutzen. Ich führe an dieser Stelle zwei willkürliche Begriffe ein: Zeilenvektor und Spaltenvektor. Der Zeilenvektor beschreibt die Zeilen einer Matrix, der Spaltenvektor deren Spalten. In Listing 4 ist also DynMatrix der Pointer auf den Zeilenvektor, DynMatrix[] sind Pointer auf die Spaltenvektoren. Der Zeilenvektor einer Matrix ist immer ein Pointer-Feld, die Spalten Vektoren sind Datenfelder. Bei einem Array 3. Ordnung sind die Spalten Vektoren, wie in Bild 3 zu sehen, hingegen auch Pointer-Felder, die dann auf die eigentlichen Datenfelder zeigen.
 Bild 3: Der Aufbau eines dreidimensionalen Feldes
Bild 3: Der Aufbau eines dreidimensionalen Feldes
Der Spaltenvektor jeder Zeile kann eine beliebige Länge besitzen, er kann sogar verkürzt oder verlängert werden. Das gleiche gilt auch für den Zeilenvektor. Nur hier ist Vorsicht geboten, denn wird er verkürzt, läßt der Programmierer damit natürlich die entsprechenden Spaltenvektoren über die Klinge springen. Damit aber nicht eventuell die Speicherverwaltung gleich mitspringt, muß der von den entsprechenden Spaltenvektoren belegte Speicher zuvor wieder freigegeben werden. Also auch in diesem Punkt wird vom Programmierer eine Menge Selbstdisziplin gefordert. Aber damit kann er den Speicher des Rechners optimal nutzen und beim Speichern von Daten die Dateigröße so klein wie möglich halten. Diese Vorteile erkauft er sich natürlich mit einem höheren Verwaltungsaufwand. In Bild 3 ist das Schema der zu Bild 2 gehörenden Speicherverwaltung zu sehen. Ausgehend von der festen Pointer-Variablen PointerName wird erst ein Pointer-Vektor und daraus eine Pointer-Tabelle erzeugt, die dann schließlich auf unsere Feldvariablen zeigt. Ein kleines Programm dazu ist in Listing 5 zu sehen.
Zum Schluß
Ich hoffe, mit diesem bescheidenen Beitrag bei einigen Lesern Licht in das Dunkel der Pointer-Welt gebracht zu haben. Ausgerüstet mit diesem Basis wissen, ist es nun sicherlich kein Ding der Unmöglichkeit, Arrays der fünften, sechsten, vielleicht 10. Dimension dynamisch zu verwalten. Das wäre allerdings vor allem eine Frage des Speicherplatzes, denn ein 10dimensionales double-Feld mit jeweils 5 Elementen hätte bereits nur für die Feldvariablen allein einen Speicherbedarf von über 93 Megabyte (!!!!!) und die Pointer benötigten dabei noch mal ungefähr 9 Megabyte, wenn eine Pointervariable zu je vier Byte, eine Variable vom Typ double zu je 10 Byte gerechnet wird.
T. W. Müller
Literatur:
- Handbuch zu TURBO C
- Paul M. Chirlian: Der Einstieg in C, Markt&Technik Verlag, 1985 ISBN 3-89090-086-0
/*
Listing 2
für Turbo C 2.0
Autor: T.W. Müller
(C) by Maxon Computer GmbH, 1994
*/
#include <stdio.h>
#include <stdlib.h>
main()
{
int *DynVektor;
int i;
DynVektor = (int *) calloc(3,sizeof(int));
if (DynVektor > NULL)
{
/* Werte berechnen */
for (i=0;i<3;DynVektor[i]=1+i++);
for (i=0;i<3;i++)
printf("\nDynVektor[%d] = %d\n",i,DynVektor[i]);
free(DynVektor);
}
getchar();
/* Sonst meckert TC.PRG nach Programmende. */
return 0;
}
Listing 2
/*
Listing 3
für Turbo C 2.0
Autor: T.W. Müller
(C) by Maxon Computer GmbH, 1994
*/
#include <stdio.h>
main()
{
int Matrix[3][3] = {{11,12,13},
{21,22,23},
{31,32,33}};
int i,j;
for (i=0;i<3;i++)
{
printf("\n");
for (j=0;j<3;printf("%d",Matrix[i][j++]));
}
getchar();
/* Sonst meckert TC.PRG nach Programmende. */
return 0;
}
Listing 3
/*
Listing 4
für Turbo C 2.0
Autor: T.W. Müller
(C) by Maxon Computer GmbH, 1994
*/
#include <stdio.h>
#include <stdlib.h>
#define Nmax 3
main()
{
int **DynMatrix;
int i,j,DimOK;
/* Den Zeilenvektor dimensionieren */
DynMatrix = (int **)calloc(Nmax,sizeof(int *));
if (DynMatrix > NULL)
{
/* Die Spaltenvektoren dimensionieren. */
for (i=0;i<Nmax;i++)
{
DynMatrixfi] = (int *)calloc(Nmax,sizeof(int));
DimOK = (DynMatrix[i] > NULL);
if (!DimOK) i=Nmax;
}
if (DimOK)
{
/* Werte berechnen */
for (i=0;i<Nmax;i++)
for (j=0;j<Nmax;
DynMatrix[i][j] = 10*(i+1)+1+j++) ;
for (i=0;i<Nmax;i++)
{
printf("\n");
for (j = 0;j<Nmax;printf("%d", DynMatrix[i][j++]));
}
for (i=0;(i<Nmax) && (DynMatrix[i] > NULL);
free(DynMatrix[i+4])) ;
free(DynMatrix);
}
}
getchar();
/* Sonst meckert TC.PRG nach Programmende. */
return 0;
}
Listing 4
/*
Listing 5
dynamische Dimensionierung eines
dreidimensionalen Feldes gemäß
Bild 3,
Autor: T.W. Müller
(C) by Maxon Computer GmbH, 1994
*/
#include „stdio.h"
#include „stdlib.h"
/* Die Kantenlange des Würfels */
#define Amax 10
/* Speicherplatz anfordern für Pointer */
#define CorePointer calloc(N,sizeof(int *))
/* Speicherplatz anfordern für Variablen */
#define CoreVars calloc(N,sizeof(int))
/* eine kleine Meldung */
#define DimOK(S) puts(".Dimension: OK")
#define NewLine printf("\n\t")
main()
{
int ***PointerName;
int Z,Y,X;
unsigned char core_OK;
int N;
N=Amax;
PointerName = ( int ***) CorePointer;
core_OK = (PointerName > NULL);
if (core_OK)
{
NewLine;
DimOK("1");
for (Z=0 ; Z<N ; Z++)
{
PointerName[Z] = ( int **) CorePointer;
core_OK= (PointerName[Z] > NULL);
if (!core_OK) Z=N;
}
if (core_OK)
{
DimOK("\t2");
for (Z=0; Z<N; Z++)
for (Y=0; Y<N; Y++)
{
PointerName[Z][Y] = ( int *) CoreVars;
core_OK= (PointerName[Z][Y] > NULL);
if (!core_OK) Y=Z=N;
}
if (core_OK)
{
DimOK("\t3");
NewLine;NewLine;
for ( Z=0; Z<N; Z++)
for (Y=0; Y<N; Y++)
for (X=0; X<N; X++)
PointerName[Z][Y][X]=100*Z+10*Y+X;
for (Z=0; Z<N; Z++)
printf ("\n\t&PointerName[%d][%d][%d] = %lu,
PointerName[%d][%d][%d] = %d",
Z,Z,Z,&PointerName[Z][Z][Z],
Z,Z,Z,PointerName[Z][Z][Z]);
puts("\n\n\nWeiter mit <Return> ...");
getchar();
printf("\n\n\tfree PointerName[Y][Z]");
for (Z = 0;(Z<N) && (PointerName[Z][Y] > NULL);Z++)
{
NewLine;
for (Y=0; Y<N; Y++)
{
free(PointerName[Z][Y]);
printf(".");
}
}
}
printf("\n\n\tfree PointerName[Z]");
NewLine;
for (Z=0;(Z<N) && (PointerName[Z] > NULL);Z++)
{
free(PointerName[Z]);
printf(".");
}
}
printf("\n\n\tfree PointerName");
free(PointerName);
}
return 0;
}
Listing 5