
Pünktlich zum 125. Todestag des Mathematikers Bernhard Riemann (1826-1866) konnte ich am 20. Juli RIEMANN II zum Testen auf meine Platte kopieren. Diese Version mit der römischen Zwei ist wie ihr Vorgänger eine LISP-ähnliche Programmiersprache mit einer beachtlichen Menge an Mathematikfunktionen.
Für diejenigen, die RIEMANN noch nicht kennen, sei hier vorab kurz erklärt, um was es dabei geht: RIEMANN II ist ein Computeralgebrasystem, das als Sprache und auch als Mathematikprogramm zur Lösung vielfältiger mathematischer Fragestellungen genutzt werden kann. Auch wenn Sie als Kind der Taschenrechnergeneration jetzt ein wenig ungläubig dreinschauen mögen, ja es ist möglich, auszurechnen, wieviel ‘2 + 3’ ist, und es ist ebenfalls möglich, das unbestimmte (sic!) Integral über seine Lieblingsfunktion zu ermitteln oder dieselbe grafisch darstellen zu lassen. Und alles dies mit dem gleichen Programm. Aber der Reihe nach.
Das Bewährte
Zuerst einmal sollte man wissen, daß RIEMANN ein Genauigkeitsfanatiker ist. Dies wird auf zwei Wegen erreicht: Einerseits ist es möglich, die Eingaben umzuformen, also aus 6/9 wird 2/3 (und eben nicht 0,666...). Andererseits kann man auch numerische Ergebnisse erzwingen (s.a. Bild 2) und erhält somit
6/9 = 0.66666666666666666666667;
multipliziert man diese Antwort dann wieder mit 3, so erhält man ‘natürlich’ das Ergebnis 2.
Verwendet man für die Aufgabenstellung nur ganze Zahlen, so kann RIEMANN bis auf die ca. 315.000ste Stelle (sic !) genau rechnen. Die größte darzustellende Zahl hätte ebenfalls soviele Stellen - da für diese Zahl aber rund 128kB Speicher benötigt würden und gut Ding eben Weile haben will, sei von der Benutzung derartiger Zahlenkolosse abgeraten (man muß ja nicht alles tun, was machbar ist).
 Bild 1. RIEMANN II, nun mit Menüangebot
Bild 1. RIEMANN II, nun mit Menüangebot
Genauso, wie Sie wahlweise eine symbolische oder numerische Verarbeitung mathematischer Terme mit RIEMANN vereinbaren können (Dialogbox in Bild 2), ist es kein Problem, für einzelne algebraische Umformungen die Vorschriften zu definieren. Man kann sich somit ein auf die individuellen Bedürfnisse abgestimmtes System schaffen. Die Krönung erfährt diese Vielfalt aber dadurch, daß man die vorhandenen Funktionen ändern (Quelltexte werden mitgeliefert) oder eigene hinzufügen kann. RIEMANN ist nach allen Seiten offen und kann - die intime Kenntnis seiner Hunderte von Funktionen oder Kontrollvariablen vorausgesetzt - beliebig angepaßt werden. Vorwegnehmen darf man vielleicht schon hier die Erkenntnis, daß mit RIEMANN (fast) alles möglich ist - man muß nur wissen, welchen Parameter man wie und wo in problemgerechter Weise einstellt.
Nachdem wir das System unseren Wünschen gemäß angepaßt haben, wollen wir jetzt mal schauen, welche Möglichkeiten sich dahinter verbergen. Stellen Sie sich einmal vor, Sie müßten eine Mathematikklausur korrigieren. Ok, ich weiß schon, was Sie denken, aber glauben Sie mir, eine Mathearbeit zu schreiben, mag schwer sein, die eines anderen nachzuschauen, kann aber zur Tortur werden. Man muß von den eigenen Überlegungen abweichende Ansätze und Lösungswege untersuchen, bei Fehlern die Folgefehler gesondert bewerten usw. Hier ist RIEMANN eine tolle Hilfe, denn man kann z.B. Gleichungen schrittweise lösen
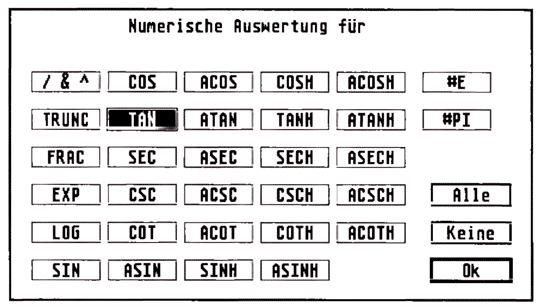
Bild 2: Wahlweise numerische Auswertung ist möglich.
@: -28 - 10 X == 21 + 60 X + 25 XA2
@+(10X==10X);
@:-28 == 21 + 70 X + 25 XA2
@+(28==28);
@: 0 == 49 + 70 X + 25 XA2
oder auch automatisch lösen lassen
SOLVE(- 28 - 10 X == 21 + 60 X + 25 X^2, X);
@:{X == -7/5};
Da auch ein beachtlicher Funktionensatz für Matrizen und Determinanten zur Verfügung steht, sind lineare Gleichungssysteme natürlich auch kein Problem:
 Bild 3: Grafische Darstellung ist Einstellungssache
Bild 3: Grafische Darstellung ist Einstellungssache
LINEQN([ 2X-4Y+Z==-8, X-Y+3Z==-16, X+2Y+3Z==-7],[X,Y,Z]);
@:[X == 5, Y == 3, Z == -6]
LINEQN([ 2X-4Y+Z==-8, X-Y+3Z==16, X+3Y+2Z==-8],[X,Y,Z]);
@:[X == ARB (1),
Y == (8 + 5 ARB (1 ))/11,
Z == (-112 - 4 ARB (1 ))/22]
(einfache unendliche Lösungsmannigfaltigkeit)
LINEQN([ 2X-4Y+Z==-8, X-Y+3Z==-16, -X-Y-8Z==10],[X,Y,Z]);
@: [] (keine Lösung, da System widersprüchlich)
Im Bereich der Infinitesimalrechnung steht neben der Bildung von Summen, Produkten und Grenzwerten die Ermittlung von Ableitungen und Integralen im Vordergrund (Kasten 1). Die mitgelieferten Zusatzpakete für Differentialgleichungen, Tensorrechnung und Vektoranalysis runden mit verschiedenen PD Routinen (Zahlentheorie, Fourier-Reihenentwicklung, Partialbruchzerlegung, Arbeiten mit Potenzreihen und für partielle Differentiale, z.B. für die Thermodynamik) das Angebot von RIEMANN II ab.
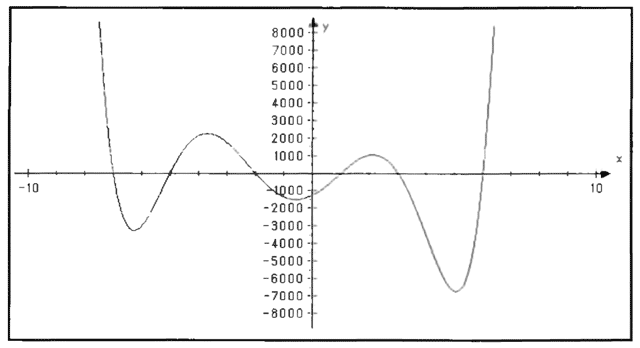 Bild 4: Der 2D-Plot kommt sauber raus.
Bild 4: Der 2D-Plot kommt sauber raus.
... und das Neue
Da der Rezensent schon einmal die Gelegenheit hatte, die Vorgängerversion von RIEMANN zu testen [ 1 ], sei hier ein kurzer Vergleich der beiden Versionen erlaubt:
RIEMANN II kann nun per Menü bedient werden (Bild 1), der Bedienungskomfort hat sich also verbessert und die Accessoires sind, sofern der Hauptspeicher ausreicht, nun auch benutzbar.
Die 2D-Grafik (Bild 4) wurde verbessert, die Parameter und Ausgabewünsche können nun über eine Dialogbox eingestellt werden (Bild 3). Um die Qualität optimal an seine Ansprüche und Wünsche anzupassen, hat man die Möglichkeit, weitere Grafikparameter einzustellen. Dies erwies sich insbesondere bei der Darstellung stetiger, aber nicht überall differenzierbarer Funktionen (z.B.f(x)=x*sin( Ux),f(x)=/x/) als notwendig. Hebbare Unstetigkeitsstellen (Lücken) werden leider nicht gekennzeichnet.
In der neuen Ausgabe können jetzt auch 3D-Grafiken von Funktionen z(x,y) angefertigt werden (Bild 5). Durch geschickte Nutzung des reichhaltigen Angebots an Grafikfunktionen und durch Änderung der Variableneinstellungen können zusätzliche Benutzerwünsche berücksichtigt werden: Vergrößern der Auflösung, wahlweise Beleuchtung oder Änderung der Betrachtungswinkel. Diese Verfeinerungen erfolgen natürlich auf Kosten der Rechenzeit und werden durch den Arbeitsspeicher beschränkt.
Da es sich bei allen Grafiken um Vektorgrafiken handelt, können sie wahlweise auf den Drucker oder in ein Metafile ausgegeben werden.
Neben der bekannten Ausgabe von mathematischen Termen steht jetzt auch die Möglichkeit des ‘pretty printing’ zur Verfügung: eine anschauliche, zweidimensionale Darstellungsform (Kasten 2).
Die Handhabung der u.U. unhandlichen Terme wird durch ein verbessertes ‘formula modelling’ vereinfacht: Terme oder Teile davon können mittels Mausklick in einen internen Speicher kopiert, gemäß der Parametereinstellungen verändert und schließlich in andere Ausdrücke eingefügt werden.
Die Sitzungen können komplett oder teilweise in einer Datei oder per Drucker protokolliert werden; eine spezielle Übergabe der Ergebnisse für eigene Programme (in einer anderen Sprache als RIE-MANN) ist ebenfalls vorhanden.
RIEMANN ist nicht kopiergeschützt, wurde aber durch ein ausgeklügeltes System individuell kodiert. Es läuft auf Rechnern der ST- und TT-Serie, die allerdings mit mindestens 1 MB RAM ausgerüstet sein sollten, da das Programm alleine schon über 570 kB auf die Waage bringt (und wenn man dann noch eines der mitgelieferten Erweiterungspakete nutzen möchte...).
Eine TOS-Version kleiner 1.4 kann mit einem Zusatzprogramm auch genutzt werden. Vom Monitor her sind alle Auflösungen verwendbar; um problemlos arbeiten zu können, sollten aber mindestens 600 Pixel horizontal zur Verfügung stehen. Eine Harddisk ist für sinnvolles Arbeiten empfehlenswert.
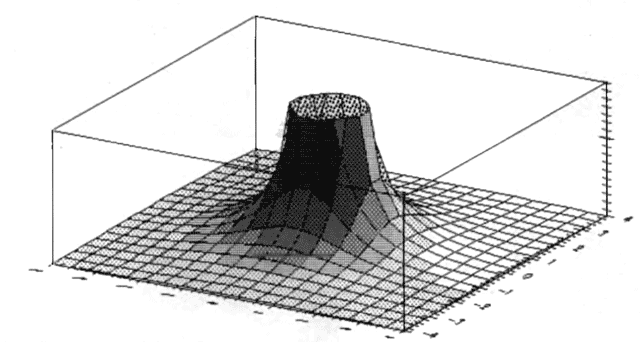 Bild 5: Dreidimensional geht's auch ...
Bild 5: Dreidimensional geht's auch ...
Zukunftswünsche
Mit Interesse konnte der Rezensent feststellen, daß die damals [ 1 ] ausgesprochene Empfehlung zur Überarbeitung der Dokumentation beherzigt wurde. Es werden nun zwei Handbücher mitgeliefert: eine Einführung (103 S.) und ein Referenzbuch (373 S.), jeweils mit eigenem Register. Der auch schon damals mitgelieferte interaktive Programmierkursus soll in seiner teilweise überarbeiteten Ausgabe die Verwendung als Sprache fördern.
Da eine optimale Nutzung der Möglichkeiten von RIEMANN erst durch die Nutzung als Programmiersprache erfolgen kann, muß die Forderung nach einer anschaulichen Einführung in diese Sprache auch heute noch ganz oben auf die Wunschliste gesetzt werden, denn das Einführungsheft erwähnt auf den 12 Seiten ‘Programmieren in RIEMANN’ verständlicherweise nur die allerwichtigsten Punkte. Genaueres kann man auf über 100 Seiten im Referenzbuch nachschauen, wo es aber, bedingt durch die Vielfalt an Möglichkeiten, nicht immer möglich war, die einzelnen Funktionen durch Beispiele zu erklären. Strenggenommen kann dies aber auch nicht Aufgabe einer Referenz sein. Wünschenswert wäre also eine ausführlichere Einführung oder - losgelöst vom Programmerwerb - eine Darstellung in Form von Sekundärliteratur zu RIEMANN.
 Kasten 1: Infinitesimalrechnung
Kasten 1: Infinitesimalrechnung
Für die Zukunft ist, wie die Programmautoren auf der diesjährigen CeBIT ankündigten, eine Schnittstelle zu TEX geplant, so daß die mathematischen Terme dort direkt eingebunden werden können.
In der für den Test vorliegenden Version 1.02 war es leider noch nicht möglich, externe Programme aufzurufen; in der aktuellen Handelsversion (V. 1.1) soll dies aber schon gelöst sein. Der Preis beträgt DM 298,-. Schüler und Studenten erhalten einen Rabatt.
RIEMANN II kann im Prinzip schon ab der Mittelstufe eingesetzt werden. Für Studenten, Lehrer, Ingenieure und alle, die sich mit Mathematik beschäftigen, aber die tägliche Routinearbeit dem Rechner überlassen möchten, kann es als wirkliche Hilfe angesehen und uneingeschränkt empfohlen werden. Wenn Sie für sich persönlich schon den Schritt vom Kopfrechnen zum Taschenrechner vollzogen haben, sollten Sie sich (und Ihrem Atari) RIEMANN II gönnen.
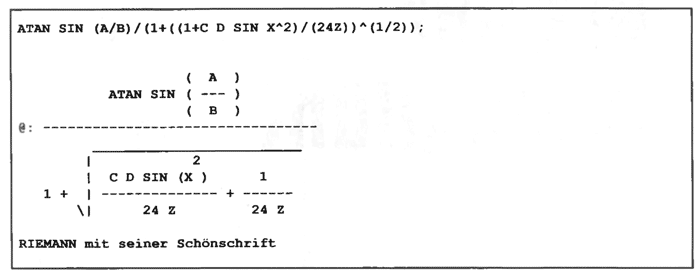 Kasten 2: ‘pretty printing’
Kasten 2: ‘pretty printing’
Literatur:
[1] Ziebarth, Harald, „Die Riemannsche Lösung ", c't 11/1990, S. 60 ff.
[2] ST-Computer, 4/1990, S. 49 ff.
[3] Bronstein; Semendjajew, „Taschenbuch der Mathematik“
Bezugsadresse:
Begemann & Niemeyer Göllnitzer Str. 12 7500 Karlsruhe 41