Viele Grafikprogramme bieten heutzutage sogenannte Bézierkurvean. Dieses „Wundermittel“ neuester Software-Kunst wurde von dem französischen Mathematiker Bézier in den siebziger Jahren für eine französische Automobilfirma entwickelt, um das Karosseriedesign mittels CAD-Programmen zu vereinfachen.
 Abb.1: allgemeine Form der Bézierkurve
Abb.1: allgemeine Form der Bézierkurve
Dieses Verfahren ermöglicht es, sogenannte Freiformkurven zwischen zwei Punkten zu ziehen, deren Verlauf durch einige Führungspunkte festgelegt wird, durch welche aber die Kurve, im Gegensatz zu Spline-Kurven [1], nicht notwendigerweise gehen muß.
Die Bézierkurve B(t) ist ein Polynom n-ten Grades, bei (n+1) gegebenen Führungspunkten, die mittels eines Parameters t erzeugt wird, d.h. jeder Parameterwert t entspricht einem Punkt der Kurve. Die allgemeine Form der Bézierkurve sieht man in Abbildung 1.
Die Abbildung 2 zeigt eine Bézierkurve, die durch vier Führungspunkte festgelegt ist. Wenn man einzelne Führungspunkte mehrfach definiert (siehe Abb. 3, pl 2fach definiert), erreicht man, daß sie einen stärkeren Einfluß auf den Verlauf der Kurve haben, sie ziehen die Kurve also mehr an sich als die übrigen Führungspunkte.
Ein Vorteil der Bézierkurven ist, daß sie, trotz vieler Führungspunkte, nie überschwingen können - im Gegensatz zu Interpolationspolynomen [2]. Dies folgt aus der weniger strengen Interpolationsforderung der Bézierkurven.
Die Definition der B(i,n) in Abbildung 1 zeigt, daß jeder Führungspunkt pi für alle t aus [0,1] Einfluß auf den Verlauf der Kurve hat. Daraus folgt, daß jeder Punkt der Bézierkurve von allen Führungspunkten abhängt, und die Kurve nicht durch ihre Führungspunkte gehen muß.
Soll eine Bézierkurve durch viele Führungspunkte bestimmt werden, bietet es sich an, die Kurve stückweise zu berechnen und dann zusammenzusetzen. Die resultierende Kurve geht dann durch die Verbindungspunkte und approximiert alle anderen Führungspunkte.
 Abb.2: Bézierkurve mit 4 Führungspunkten
Abb.2: Bézierkurve mit 4 Führungspunkten
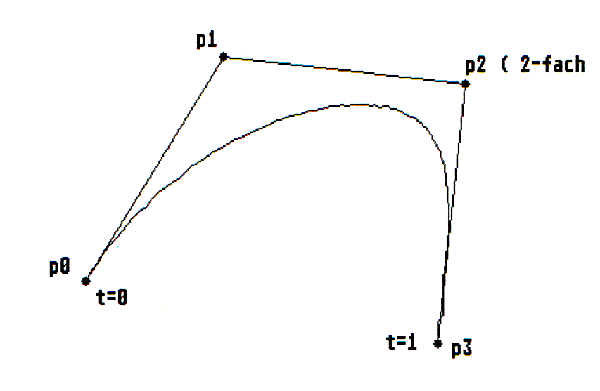 Abb.3: Bézierkurve mit 5 Führungspunkten
Abb.3: Bézierkurve mit 5 Führungspunkten
Die Tangenten in den Endpunkten der Bézierkurve stimmen mit der geraden Verbindung zum vorhergehenden Führungspunkt überein. Wenn man nun einen glatten Übergang zwischen zwei Bézierkurven haben möchte, muß man nur zusätzlich geeignete Führungspunkte einfügen (Abb. 4).
Solche glatten Übergänge erhält man zum Beispiel, wenn sich die Punkte auf einer Geraden befinden und der mittlere der Verbindungspunkt ist. Es gibt also zwei verschiedene Möglichkeiten, glatte Übergänge zwischen zwei Bézierkurven zu schaffen: entweder zwischen zwei Punkten einen dritten einfügen oder auf beiden Seiten des Verbindungspunktes je einen Punkt wählen.
Die numerische Berechnung von Bézierkurven kann durch ein iteratives Verfahren vereinfacht werden (Abb. 5 / siehe auch [3]). Ausgehend von (n+1) Führungspunkten multipliziert man für jeden Kurvenparameter t die Koordinaten x und y des i-ten Punktes mit (1 - t) und des (i + 1)-ten Punktes mit t. Die Summe ergibt den neuen Wert p(i,i+1), insgesamt erhält man (n + 1)-1 Werte. Dieses Verfahren wendet man n-mal an, bis man nur noch einen Punkt erhält. Dies ist dann der gesuchte Kurvenpunkt.
Das Omikron.BASIC-Programm (Listing 1) zeichnet eine Bézierkurve für beliebig viele Führungspunkte, wobei mehr als 8 Punkte ungeeignet sind, da sonst die Rechenzeit zu sehr steigt und die Genauigkeit (Variable delta) erhöht werden müßte.
 Abb.4: Drei zusammengesetzte Bézierkurven mit glatten Übergängen
Abb.4: Drei zusammengesetzte Bézierkurven mit glatten Übergängen
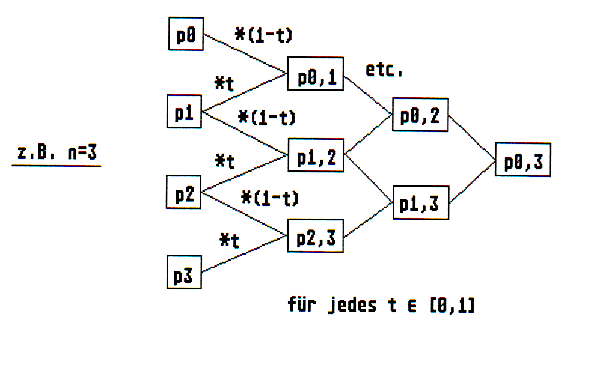 Abb.5: Numerische Berechnung von Bézierkurven
Abb.5: Numerische Berechnung von Bézierkurven
[1] Dietmar Rabich: Rund muß es sein, ST-Computer 1/89
[2] Dietmar Rabich: Numerische Mathematik, Teil 2: Interpolation, ST-Computer 10/89
[3] H. Kopp: Grafische Datenverarbeitung, Hanser-Verlag
[4] W. Luther, M. Ohsmann: Mathematische Grundlagen der Computergraphik, Vieweg-Verlag
[5] W. Purgathofer: Graphische Datenverarbeitung, Springer-Verlag
' ****************************************
' * Bézier - Kurven *
' * Listing 1 *
' * Autor: Kai Hendrik Komp *
' ****************************************
INPUT "Anzahl der Führungspunkte: ";N:N=N-1
PRINT "Mit Mauszeiger Punkt markieren und"
PRINT "linke Maustaste drücken !"
DIM Px(N),Py(N),Qx(N),Qy(N),Rx(N),Ry(N)
'
MOUSEON
FOR I%=0 TO N
REPEAT
Px(I%)= MOUSEX
Py(I%)= MOUSEY
UNTIL MOUSEBUT =1
WAIT .75
MOUSEOFF
PCIRCLE Px(I%),Py(I%),3
IF I%<>0 THEN
DRAW Px(I%-1),Py(I%-1) TO Px(I%),Py(I%)
ENDIF
MOUSEON
NEXT I%
'
' bestimmt Anzahl der zu berechnenden Pkte
Delta!=.01
'
Xold=Px(0):Yold=Py(0)
'
T=-Delta!
WHILE T<1
T=T+Delta!
M=N
FOR I%=0 TO M
Qx(I%)=Px(I%)
Qy(I%)=Py(I%)
NEXT I%
WHILE M>0
FOR J%=0 TO M-1
Rx(J%)=Qx(J%)+T*(Qx(J%+1)-Qx(J%))
Ry(J%)=Qy(J%)+T*(Qy(J%+1)-Qy(J%))
NEXT J%
M=M-1
FOR J%=0 TO M
Qx(J%)=Rx(J%)
Qy(J%)=Ry(J%)
NEXT J%
WEND
DRAW Xold,Yold TO Qx(0),Qy{0)
Xold=Qx(0):Yold=Qy(0)
WEND