 Abb. 1a und b: Simulation einer semipermeablen Zellmembran (schwarz): Die roten Punkte stellen Nährstoffe, die grünen Giftstoffe dar. Zuerst ist die Zelle leer, nach einer bestimmten Zeit aber hat sich die Konzentration von Nährstoffen innerhalb der Zelle der Außenkonzentration angepaßt. Nicht so für die Giftstoffe. Für sie ist die Membran undurchlässig.
Abb. 1a und b: Simulation einer semipermeablen Zellmembran (schwarz): Die roten Punkte stellen Nährstoffe, die grünen Giftstoffe dar. Zuerst ist die Zelle leer, nach einer bestimmten Zeit aber hat sich die Konzentration von Nährstoffen innerhalb der Zelle der Außenkonzentration angepaßt. Nicht so für die Giftstoffe. Für sie ist die Membran undurchlässig.
Im Gegensatz zu herkömmlichen Simulationskonzepten gibt es eine neue Idee namens CAM. Cellular Automata Machines arbeiten auf rein graphischer Ebene. Ihren Ursprung hatten sie in der Entdeckung des Life-Spiels, sie sind aber heute schon in der Lag?, komplexe natürliche Vorgänge zu simulieren.
Simulationen sind nach wie vor eines der faszinierenden Anwendungsgebiete von Computern. Man denke an Fahr- und Flugsimulatoren, Windkanäle auf dem Bildschirm oder Simulationen des Sternenhimmels, um nur einige Beispiele zu nennen. So verschieden die Anwendungen auch sein mögen, eins haben die Simulationsprogramme gemein: Sie sind alle nur für bestimmte Simulationen ausgelegt. Ein Fahrsimulator kann kein Flugzeug, ein Windkanal keinen Sternenhimmel nachahmen. Das ist auch ganz verständlich, denn der dem Programm zugrunde liegende Algorithmus ist spezifisch für eine Aufgabenstellung konzipiert. Bei solchen Programmen werden die Änderungen des zu simulierenden Systems zuerst mathematisch erfaßt und berechnet, und erst in einem zweiten Schritt werden sie auf dem Bildschirm sichtbar gemacht. Über Differentialgleichungen werden z.B. die Geschwindigkeiten (und Richtungen) von Molekülen bzw. etwas größeren Einheiten (“Luftpaketen”), die sich über eine Karosserie bewegen, errechnet und dann graphisch angezeigt.
Vom Pixel zum Prinzip
Eine CAM arbeitet nach einem ganz anderen Prinzip: Viele komplexe Vorgänge in der Natur können nämlich als lokale Wechselwirkungen benachbarter Partikel begriffen werden. Dabei kann es sich sowohl um biologische, chemische, physikalische als auch um geographische, meteorologische und ökonomische Probleme handeln. Eine CAM reduziert die globalen und komplexen Vorgänge auf kleine lokale Einheiten mit einfachen Regeln der Umformung. Die Berechnung eines neuen Zustandes basiert dabei auf der rein graphischen Umformung auf lokaler Ebene. Das CAM-Programm errechnet dazu den Farbwert eines jeden Pixels auf dem Bildschirm aus den Farbwerten der benachbarten Pixel, wobei es sich nach vorgegebenen Regeln richtet.
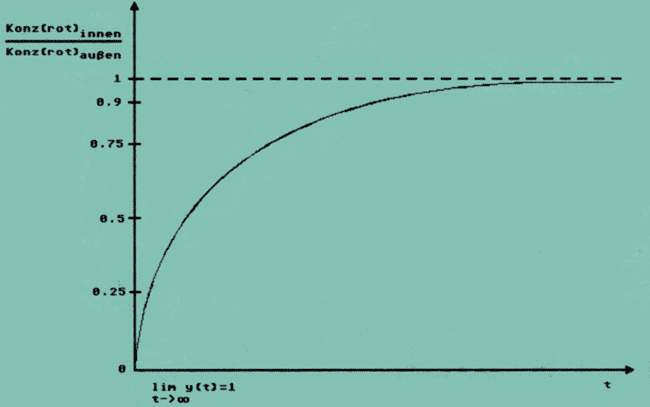 Abb. 2: Abhängigkeit der Konzentration des Nährstoffes innerhalb der Zelle von der Zeit. Der rote Graph wurde durch jeweiliges Zählen der Punkte bei der CAM-Simulation ermittelt, der blaue Graph ergibt sich aus der Lösung der Differentialgleichung, die solche Diffusionsphänomene beschreibt (Ficksches Gesetz).
Abb. 2: Abhängigkeit der Konzentration des Nährstoffes innerhalb der Zelle von der Zeit. Der rote Graph wurde durch jeweiliges Zählen der Punkte bei der CAM-Simulation ermittelt, der blaue Graph ergibt sich aus der Lösung der Differentialgleichung, die solche Diffusionsphänomene beschreibt (Ficksches Gesetz).
Game of Life
Als historisch bekanntestes Beispiel für eine primitive CAM sei hier das Life-Spiel von Conway erwähnt. Bei ihm gibt es 2 Pixelzustände:
1 = angeschaltet = "lebendig",
0 = ausgeschaltet = "tot".
Seine Regel besagt, daß ein Pixel dann ausgeschaltet wird, wenn weniger als 2 und mehr als 3 Nachbarn angeschaltet sind. Bei genau 2 “lebenden” Nachbarpixein bzw. -zellen wird das im Zentrum liegende Pixel (“center cell”) nicht verändert, bei 3 angeschalteten Nachbarn wird es angeschaltet, sofern es vorher ausgeschaltet war. Um zu unserem Windkanal zurückzukehren: Zur Berechnung eines Luftpaketes wird nicht auf Differentialgleichungen zurückgegriffen, sondern es wird die lokale Umgebung der Partikel (Pixel) abgefragt und danach der neue Zustand bestimmt. Was auf lokaler Ebene nach überschaubaren Gesetzen abläuft, hat im übergeordneten Rahmen plötzlich komplexe Vorgänge zur Folge. Weil dies ein elementares Prinzip in der Natur darstellt, läßt sich eine CAM auf die verschiedensten Gebiete anwenden. Je nachdem, welche Vorgänge man simulieren möchte, kann man verschiedene Nachbarschaftsbeziehungen definieren.
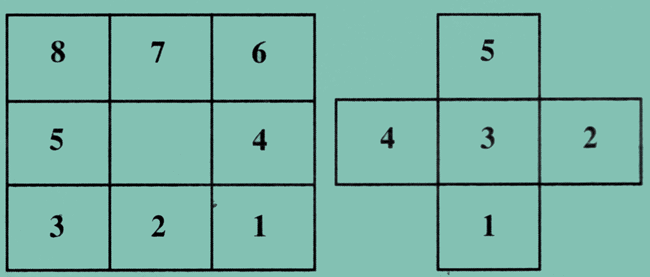 Abb. 3: Links Moore-Nachbarschaftbeziehung, rechts Von Neumann-Nachbarschaft.
Abb. 3: Links Moore-Nachbarschaftbeziehung, rechts Von Neumann-Nachbarschaft.
Die Nachbarschaft des Herrn Moore
Die im Life-Spiel benutzte Nachbarschaft besteht aus den 8 direkten Nachbarzellen, die eine center cell hat. Sie nennt sich Moore-Nachbarschaft (Abb. 3). Im Life-Spiel ist sie relativ definiert, d.h. es kommt bei der Berechnung nur darauf an, wieviele Zellen jeweils angeschaltet sind, nicht aber, wo sie absolut positioniert sind. Mit dieser Nachbarschaftsbeziehung lassen sich vor allen Dingen Wachstumsprozesse (z.B. Kristall Wachstum) simulieren und experimentelle Graphiken wie Fractale erzeugen (siehe Abbildung 4). Eine Regel im relativen Moore-Modus zeigt Abbildung 5.
Will man dagegen asymmetrische Prozesse ablaufen lassen wie etwa die Veränderung einer Insel an ihrer Westküste (Abbildung 6), so muß man sich der absoluten Moore-Nachbar schaft bedienen. Sie bietet sehr viel mehr Möglichkeiten, erfordert dafür aber auch mehr Zeit bei der Eingabe der Regel. Bei 2 Pixelzuständen (an und aus bzw. 1 und 0) sind nämlich nicht mehr bloß 9 mögliche Umgebungen (0-8 Pixel 8 angeschaltet, Rest ausgeschaltet), sondern 2 ^ 8 = 256 vorhanden.
 Abb. 4: Dieses Fractal wurde mit Hilfe der relativen Moore-Nachbarschaft erzeugt. Man erkennt deutlich die Strukturen, die sich sowohl im Kleinen als auch im Großen wiederfinden.
Abb. 4: Dieses Fractal wurde mit Hilfe der relativen Moore-Nachbarschaft erzeugt. Man erkennt deutlich die Strukturen, die sich sowohl im Kleinen als auch im Großen wiederfinden.
Die Margolus-Nachbarschaft
Für die Darstellung kinetischer Vorgänge im allgemeinen, Molekülbewegungen im speziellen, eignet sich besonders die sogenannte Margolus-Nachbarschaft. Bei ihr werden nicht einzelne Pixel und deren Umgebungen betrachtet, sondern 4-Pixel-Blöcke. Diese werden bei der Berechnung eines neuen Bildes durch vorher vom Benutzer zugewiesene neue 4er Blöcke ersetzt. Bei 2 Pixelzuständen gibt es 2^4=16 mögliche Pixelkombinationen in einem 4er-Block. Als Beispiel für eine Zuweisung kann man in Abbildung 7 eine vollständige Regel zur Simulation eines Gases sehen.
Es läßt sich zeigen, daß ein nach diesen Gesetzen existierendes Gas elementare Gesetze der Thermodynamik erfüllt. Dazu zählen Impuls-, Energie- und Masseerhaltung. Aber selbst differenziertere Aspekte wie die mittlere freie Weglänge lassen sich berechnen.
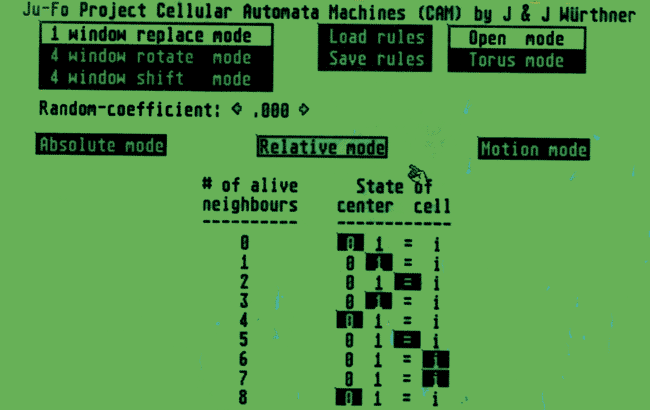 Abb. 5: So sieht eine Regel für die relative Moore-Nachbarschaft aus. Links steht die Anzahl der angeschalteten Nachbarzellen (0-8), rechts davon kann der Benutzer angeben, was jeweils mit der center cell passieren soll (0: ausschalten; 1: einschalten; = : nicht verändern; i: invertieren).
Abb. 5: So sieht eine Regel für die relative Moore-Nachbarschaft aus. Links steht die Anzahl der angeschalteten Nachbarzellen (0-8), rechts davon kann der Benutzer angeben, was jeweils mit der center cell passieren soll (0: ausschalten; 1: einschalten; = : nicht verändern; i: invertieren).
Wie funktioniert die Margolus-Nachbarschaft nun genau? Es reicht nicht, die 4er-Blöcke, wie beschrieben, nur auszutauschen. Denn was passiert z.B. mit  ? Er wird in der Folgegeneration, d.h. im nächsten Bild, zu
? Er wird in der Folgegeneration, d.h. im nächsten Bild, zu  , der Punkt “fliegt” also nach oben. Im nächsten Durchgang wird dieser 4er-Block jedoch wieder durch
, der Punkt “fliegt” also nach oben. Im nächsten Durchgang wird dieser 4er-Block jedoch wieder durch  ersetzt (siehe Regel oben), so daß der Punkt zurückfliegt. Entsprechendes geschieht mit allen anderen Pixeln. Man erhält so ein System, das ständig zwischen zwei Zuständen hin- und herpendelt. Mit einem Gas hat dies recht wenig zu tun. Mit einem Trick kann man es jedoch schaffen, daß ein Punkt solange seine ursprüngliche Richtung beibehält, bis er mit einem anderen zusammenstößt. Dies erreicht man dadurch, daß man die Eckpunkte der 4er- Blocks pro Generation immer um einen Punkt nach unten und nach rechts verschiebt. Man könnte auch sagen, daß man zwei imaginäre Gitter über den Bildschirm spannt. Die 4er-Blöcke haben nun jede 2te Generation ihre Eckpunkte auf geraden x/y-Gitterpunkten, jede dazwischenliegende Generation jedoch auf ungeraden Gitterpunkten. Das hat zur Folge, daß sich ein Punkt, der gerade von rechts unten nach links oben innerhalb eines 4er-Blockes gewandert ist, in der Folgegeneration wieder in der unteren rechten Ecke eines 4er Blocks befindet. Er wird daher erneut nach links oben wandern usw. (siehe Abb. 8).
ersetzt (siehe Regel oben), so daß der Punkt zurückfliegt. Entsprechendes geschieht mit allen anderen Pixeln. Man erhält so ein System, das ständig zwischen zwei Zuständen hin- und herpendelt. Mit einem Gas hat dies recht wenig zu tun. Mit einem Trick kann man es jedoch schaffen, daß ein Punkt solange seine ursprüngliche Richtung beibehält, bis er mit einem anderen zusammenstößt. Dies erreicht man dadurch, daß man die Eckpunkte der 4er- Blocks pro Generation immer um einen Punkt nach unten und nach rechts verschiebt. Man könnte auch sagen, daß man zwei imaginäre Gitter über den Bildschirm spannt. Die 4er-Blöcke haben nun jede 2te Generation ihre Eckpunkte auf geraden x/y-Gitterpunkten, jede dazwischenliegende Generation jedoch auf ungeraden Gitterpunkten. Das hat zur Folge, daß sich ein Punkt, der gerade von rechts unten nach links oben innerhalb eines 4er-Blockes gewandert ist, in der Folgegeneration wieder in der unteren rechten Ecke eines 4er Blocks befindet. Er wird daher erneut nach links oben wandern usw. (siehe Abb. 8).
In der Wahl von Nachbarschaften sind einem kaum Grenzen gesetzt. Man muß nur bedenken, daß sich die Anzahl der einzugebenden Regeln mit jeder hinzukommenden Nachbarschaftszelle verdoppelt, bzw. bei n Pixelzuständen (n Farben) ver’n’-facht.
Die Von Neumann-Nachbarschaft
Der Vollständigkeit halber sei hier noch die Von Neumannsche Nachbarschaft angeführt. Bei ihr werden zur Bestimmung der center cell die 4 direkten Nachbarzellen (oben, unten, rechts, links) und der Zustand der center cell selbst herangezogen (Abb. 3). Eine Anwendung dieser Nachbarschaft liegt in der “Banks Regel”, die im Prinzip Ecken löscht und Lücken füllt. Mit dieser Regel als Grundlage können nun Impulsgeneratoren, Frequenzteiler, Drähte usw. aufgebaut werden, mit denen wiederum die Konstruktion eines “graphischen Computers” möglich erscheint. Allerdings müßte dazu der Bildschirm wesentlich größer sein. Wir stoßen hier auf eine interessante Frage der theoretischen Informatik: Ist es möglich, auf einer CAM eine universelle Rechenmaschine, also einen Computer, der jedes in endlicher Zeit berechenbare Problem lösen kann, zu konstruieren? Von Neumann bewies, daß bestimmte Regelsysteme, u.a. Conway's Game of Life, diese Fähigkeit besitzen.
Ohne Theorie geht’s auch hier nicht (so gut)
Nun noch zu zwei weiteren theoretischen Aspekten: Zeit ist in einer CAM diskret, d.h. sie läuft nicht kontinuierlich, sondern springt von einer Stufe zur nächsten. Die kleinste Zeiteinheit ist der Aufbau eines neuen Bildes aus dem alten und wird als eine Generation bezeichnet. Der zweite wichtige Aspekt einer CAM ist, daß es keinen Algorithmus gibt, um das Ergebnis schneller zu berechnen, als die CAM mit ihrer jeweiligen Regel, d.h. um von einem Ausgangszustand die Generation x zu erhalten, muß man die CAM tatsächlich x Generationen rechnen lassen und selbst ruhig zuschauen. Man kann diesen Prozeß nicht abkürzen. Weil sich der Zustand der Pixel nur nach ihren lokalen Umgebungen richtet, machen sich Veränderungen in bestimmten Bereichen erst nach einiger Zeit in entfernten Regionen bemerkbar, ein Vorgang, der von der Natur bestätigt wird. Man spricht in diesem Zusammenhang von Lichtgeschwindigkeit, das ist die größtmögliche Geschwindigkeit, mit der sich Störungen/Veränderungen ausbreiten können. Mit der Moorschen und der Von Neumannschen Nachbarschaft beträgt die Lichtgeschwindigkeit z.B. 1 Pixel pro Generation. Je nachdem, wie weit die Nachbarschaften um die center cell gefaßt sind, ergibt sich ein bestimmter “Lichtkegel", ein Bereich, auf den ein Vorgang in einem bestimmten Zeitraum Auswirkungen haben kann:
Jedem seine CAM
Hier nun eine Anleitung zur Programmierung einer einfachen CAM:
Eine einfache CAM besteht aus drei Hauptteilen:
- einem Modul zur Erstellung der Ausgangssituation,
- einem Modul zur Bestimmung der Nachbarschaft und Eingabe der Regeln,
- einem Ausführungsmechanismus, der die Regeln auf die Ausgangssituation anwendet.
Bei 1. handelt es sich um eine Art Zeichenprogramm mit u.U. speziellen Funktionen für CAM. Beim zweiten Modul ist darauf zu achten, daß es möglichst eingabefreundlich ist, denn in ihm verbringt der Anwender die meiste Zeit. Seine Funktion besteht darin, die eingegebenen Regeln in Regeltabellen festzuhalten. Der Ausführungsmechanismus liest dann aus diesen Tabellen den einer bestimmten Kombination entsprechenden Wert und “färbt” damit die center cell. Das sollte möglichst flott gehen, denn bei einem Bildschirm mit 20000 bis 40000 Punkten oder noch mehr werden sonst die Nächte lang. Der Ausführungsmechanismus sollte also maschinennah, am besten also in Assembler, programmiert werden (Raten Sie mal, was wir die letzten 15 Monate gemacht haben?!)
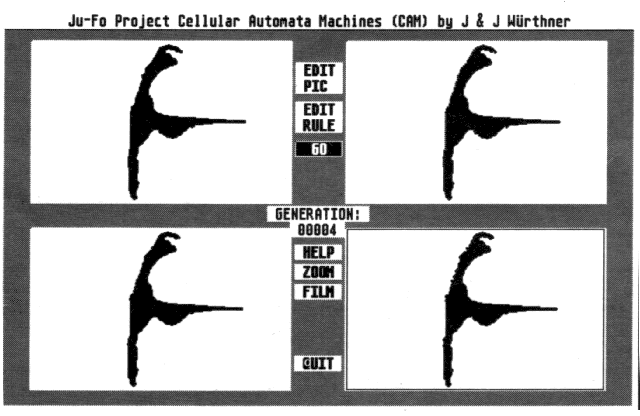 Abb. 6: Veränderung einer Küste, hier am Beispiel Sylt. Keine Panik, so weit ist es noch nicht und wird es wohl auch nicht kommen. Hiermit soll nur gezeigt werden, daß eine CAM im Prinzip auch auf solche Problemstellungen angewendet werden kann.
Abb. 6: Veränderung einer Küste, hier am Beispiel Sylt. Keine Panik, so weit ist es noch nicht und wird es wohl auch nicht kommen. Hiermit soll nur gezeigt werden, daß eine CAM im Prinzip auch auf solche Problemstellungen angewendet werden kann.
Beispielprogramm
Um den Einstieg etwas zu erleichtern, hier nun eine einfache CAM in Omikron.BASIC. Sie besitzt 2 Nachbarschaftsbeziehungen:
- die Moore-Nachbarschaft,
- die Margolus-Nachbarschaft.
Nach dem Starten kann zwischen diesen beiden Nachbarschaften gewählt werden. Danach erscheint eine 38*22 Matrix, auf der mittels Maus ein Muster eingegeben werden kann (links malen, rechts löschen). Wenn beide Mausknöpfe gleichzeitig gedrückt werden, wird der Verarbeitungsmechanismus ausgelöst. Gestoppt wird die Abarbeitung durch Drücken des rechten Mausknopfes.
Um das Programm nicht allzulang werden zu lassen, haben wir die Routine zur Veränderung der Regel weggelassen. Deshalb müssen Sie, wenn Sie experimentieren wollen, die Datazeilen 19 und 20 abändern. Die erste dieser Zeilen enthält die Regel für die Moore-Nachbarschaft, die zweite die Regel für die Margolus-Nachbarschaft. Dabei sind folgende Regeln vorgegeben: Zeile 19: Life-Spiel; Zeile 20: Gas-Gesetz, d.h. Ausbreitung von Gasmolekülen nach der oben beschriebenen Regel. Die Zahlen haben für die Moore-Nachbarschaft folgende Bedeutung:
- Stelle: Verhalten des Pixels bei 0 angeschalteten Nachbarn,
- Stelle: Verhalten des Pixels bei einem angeschalteten Nachbarn,
- Stelle: .... bei 2, ....,
- Stelle: Verhalten bei 8 angeschalteten Nachbarn.
Dabei gibt es 3 Möglichkeiten für das gerade erwähnte Verhalten des Pixels (center cell pixel):
0= Pixel wird ausgeschaltet,
1= Pixel wird angeschaltet,
2= Pixelzustand bleibt unverändert
Für die Margolus-Nachbarschaft haben die Zahlen eine andere Bedeutung: Wie weiter oben beschrieben, gibt es bei einem Schwarzweißprogramm 16 verschiedene 4er-Kombinationen. Jede Kombination wird repräsentiert durch eine Stelle in der Datazeile:

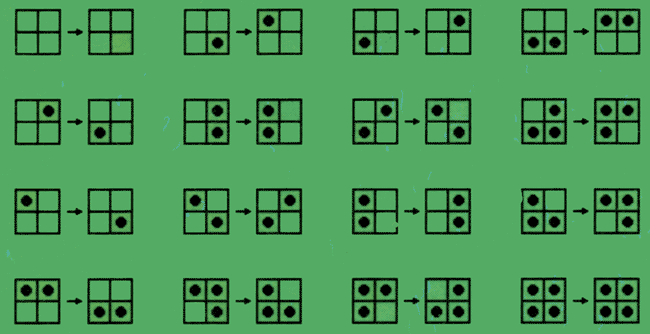 Abb. 7: Eine Regel zur Gassimulation in der Margolus-Nachbarschaft. Rechts stehen die 4er-Blocke, mit denen die Ausgangspixelblocks (links) ausgetauscht werden.
Abb. 7: Eine Regel zur Gassimulation in der Margolus-Nachbarschaft. Rechts stehen die 4er-Blocke, mit denen die Ausgangspixelblocks (links) ausgetauscht werden.
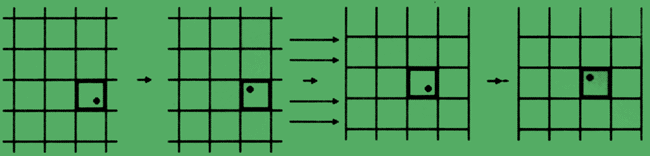 Abb. 8: Wanderung eines Pixels über den Bildschirm; sie wird möglich, weil sich zwei Gitter, die etwas gegeneinander verschoben sind, in der Steuerung des Punktes abwechseln.
Abb. 8: Wanderung eines Pixels über den Bildschirm; sie wird möglich, weil sich zwei Gitter, die etwas gegeneinander verschoben sind, in der Steuerung des Punktes abwechseln.
Dabei haben die eingetragenen Zahlen diese Bedeutung:
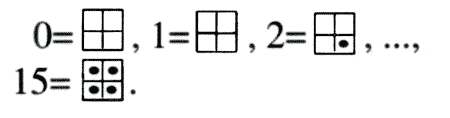
Jeder Block wird durch den Block ausgetauscht, den die Zahl in der Datazeile repräsentiert.
Nun noch zur Erklärung der einzelnen Programmteile:
Hauptprogramm:
Zeilen 0-4: Einlesen der Datenelemente in Felder;
Zeilen 5-17: Auswahl der Nachbarschaft und Bildschirmaufbau
Unterprogramme:
Zeilen 22-27: Initialisierung des CAM-Bildschirmes
Zeilen 30-42: Eingabe des Musters über die Maus
Zeilen 43-62: Verarbeitungsmechanismus für Moore-Nachbarschaft
Zeilen 63-67: Zähler für angeschaltete Nachbarzellen
Zeilen 69-99: Verarbeitungsmechanismus für Margolus-Nachbarschaft.
Zu Beginn der Verarbeitungsroutinen wird jeweils die linke Bildschirmseite nach rechts kopiert. Die Untersuchung der Pixelumgebungen findet auf dem Ursprungsbild (links) statt, die Veränderungen der Pixel selbst werden auf der rechten Seite durchgeführt. Diese Trennung ist deshalb notwendig, weil ja zur Berechnung eines neuen Pixelzustandes die Umgebung des Pixels in der Generation vorher herangezogen werden soll, und nicht die, die sich gerade in der laufenden Berechnung ergibt.
Nachdem alle Pixel auf der rechten Seite entsprechend der Regel gesetzt worden sind, wird diese rechte Seite nach links kopiert und damit zum Ausgangszustand für die Berechnung der nächsten Generation.
 Abb. 9: Störungen in einer CAM breiten sich aus. Dadurch ergibt sich ein Bereich (Lichtkegel), auf den ein Vorgang nach bestimmter Zeit eine Auswirkung hat.
Abb. 9: Störungen in einer CAM breiten sich aus. Dadurch ergibt sich ein Bereich (Lichtkegel), auf den ein Vorgang nach bestimmter Zeit eine Auswirkung hat.
Fazit
CAMs bieten eine Vielzahl von Anwendungsmöglichkeiten. Sie stellen dem Anwender eine Art Labor zur Verfügung, in dem er Experimente entwerfen und durchführen kann. Er kann sowohl künstliche Universen kreieren, in denen Gesetze gelten, die er bestimmt, als auch natürliche Vorgänge nachbilden. Da die Berechnung vieler Pixels (Pixel Updates) auch simultan erfolgen kann, ist eine CAM geradezu prädestiniert, auf Parallelrechnern wie der Connection Machine oder einem Transputer zu laufen. In der zukünftigen Erforschung komplexer Systeme werden demnach CAMs und ihre graphischen Darstellungen anstelle reiner Rechnungen eine wachsende Rolle spielen.
Jens und Jan Würthner
Quellen:
- Cellular Automata Machines, von Tommaso Toffoli und Norman Margolus, MIT press (c) 1987
- Cellular Automata ’86 Conference manual, von Charles Bennet, Tommaso Toffoli, Stephen Wolfram
1 Xecke%L=8:Yecke%L=16:' Variableninitialisierung
2 FOR I%L=1 TO 9: READ Rule%L(I%L): NEXT I%L:'lese Moore-Regel
3 DIM Mrule%L(16)
4 FOR I%L=1 TO 16: READ Mrule%L(I%L): NEXT I%L:'lese Margolus-Regel
5-Anfang
6 CLS
7 PRINT "(1) MOORE-NACHBARSCHAFT (2) MARGOLUS-NACHBARSCHAFT"
8 INPUT Opt%L:' Wahl zwischen Nachbarschaften
9 CLS
10 Scr_Init:' Bildschirmaufbau
11 PRINT CHR$(27);"f";
12 Edit_Scr:' Edierung der Ausgangsbildes mit Maus
13 PRINT CHR$(27);"e";
14 'Input_Opt
15 IF Opt%L=1 THEN Go:' Ausfuehrung d.Moore-Nachbarsch.
16 IF Opt%L=2 THEN Gomarg:' Ausfuehrung der Margolus-Nachbarschaft
17 GOTO Anfang
18 '
19 DATA 0,0,2,1,0,0,0,0,0:' Regel fuer Moore-Nachbarschaft:Life-Spiel
20 DATA 0,8,4,12,2,10,9,14,1,6,5,13,3,11,7,15:'Regel fuer Margolus-Nachbarschaft:Gas-Gesetz
21 '
22 DEF PROC Scr_Init:' Routine zum CAM-Bildschirmaufbau
23 PRINT
24 FOR I%L=1 TO 23:' 38x23 Matrix
25 PRINT " ...................................... "
26 NEXT I%L
27 RETURN
28 '
29 '
30 DEF PROC Edit_Scr:' Aenderung d.Ausgangsbildes
31 MOUSEON
32 WHILE MOUSEBUT <>3:' Verlassen der Routine durch Druecken beider Mausknoepfe
33 IF MOUSEBUT =0 THEN GOTO Es_Ende
34 X%L=( MOUSEX -3)/8:Y%L=( MOUSEY -5)/16
35 IF X%L>38 OR Y%L>23 THEN GOTO Es_Ende
36 MOUSEOFF :' Linker Mausknopf: Zeichnen, rechter Mausknopf: Loeschen
37 PRINT @(Y%L,X%L); CHR$(-46*( MOUSEBUT =2)-42*( MOUSEBUT =1));
38 MOUSEON
39-Es_Ende
40 WEND
41 MOUSEOFF
42 RETURN
43 DEF PROC Go:' Routine zur Ausfuehrung der Moore-Nachbarschaft
44 ' Verlassen d.Routine durch Druecken d.r.Mausknopfes
45 WHILE MOUSEBUT <>2
46 BITBLT 0,0,320,400 TO 320,0,320,400:' Kopieren des Bildschirmes
47 FOR Iy%L=1 TO 23:' 23 Reihen, Y-Schleife
48 FOR Jx%L=41 TO 78:' 38 Spalten,X-Schleife
49 Zaehler%L=0:' Zaehlen der Nachbarn
50 J2%L=Jx%L-1: FOR Vertical%L-Iy%L-1 TO Iy%L+1: Calc: NEXT Vertical%L:' vordere Pixel
51 J2%L=Jx%L: Vertical%L*=Iy%L-1: Calc:Vertical%L=Iy%L+1:Calc:' mittl.2 Pixel
52 J2%L=Jx%L+1: FOR Vertical%L=Iy%L-1 TO Iy%L+l: Calc: NEXT Vertical%L:' hintere 3 Pixel
53 Rule%L=Rule%L(Zaehler%L+1):'Lese neuen Wert
54 IF Rule%L>1 THEN GOTO Weiter:' Bei Wert=2: Pixel unverändert
55 REM PRINT @(Iy,Jx-40);CHR$(-42*(Rule(Zaehler)=1)-46*(Rule(Zaehler)=0)-(Rule(Zaehler)=2)*(-46*(POINT(J*8+4,1*16+8)=1)-42*( POINT(J*8+4,I*16+8)=0)))
56 PRINT @(0,0);Rule%L
57 PRINT @(Iy%L,Jx%L-40); CHR$(-42*(Rule%L=1)-46*(Rule%L=0)):' Bei Wert=1:Print "*"
58-Weiter:' Bei Wert=0:Print
59 NEXT Jx%L
60 NEXT Iy%L
61 WEND
62 RETURN
63 DEF PROC Calc:' Zaehlen d.angeschalt.Nachbarn
64 I1%L=Vertical%L-23*(Vertical%L=0)+23*(Vertical%L=24)
65 J1%L=J2%L-38*(J2%L=40)+38*(J2%L=79)
66 Zaehler%L=Zaehler%L+(POINT(J1%L*8+3,I1%L*16+7))
67 RETURN
68 '
69 DEF PROC Gomarg:' Routine z.Ausfuehrung d. Margolus-Nachbarschaft
70 WHILE MOUSEBUT <>2:' Verlassen d.Routine d.Druecken d.rechten Mausknopfes
71 '
72 FOR I%L=0 TO 1:' Es gibt zwei Gitter in diesem Modus:0 und 1
73 BITBLT 0,0,320,400 TO 320,0,320,400:' Kopieren des Bildschirmes
74 FOR J%L=I%L TO 38+I%L-1 STEP 2:'Y-Schleife
75 FOR K%L=I%L TO 22+I%L-1 STEP 2:'X-Schleife
76 Xpointer%L=Xecke%L+8*J%L+3:'Xpointer,Ypointer = Offset
77 Ypointer%L=Yecke%L+16*K%L+7
78 S2%L=40*8:' S2 = Screen2
79 Test1%L= POINT(Xpointer%L+S2%L,Ypointer%L):' Die 4 Bits werden in Tabkombination zusammengestellt
80 Test2%L= POINT(Xpointer%L-8+S2%L,Ypointer%L)
81 Test3%L= POINT(Xpointer%L+S2%L,Ypointer%L-16)
82 Test4%L= POINT(Xpointer%L-8+S2%L,Ypointer%L-16)
83 Tabkombination%L=Test1%L+2*Test2%L+4*Test3%L+8*Test4%L
84 Tabwert%L=Mrule%L(Tabkombination%L+1):' Lese neuen Wert
85 Wert1%L=Tabwert%L AND 1:' In Wert1..Wert4 sind die neuen Bits|
86 Wert2%L=(Tabwert%L AND 2)/2
87 Wert3%L=(Tabwert%L AND 4)/4
88 Wert4%L=(Tabwert%L AND 8)/8
89 Xpointer%L=(Xpointer%L-3)/8:' Neuer Offset
90 Ypointer%L=(Ypointer%L-7)/16
91 PRINT @(Ypointer%L,Xpointer%L);CHR$(-42*(Wertl%L=l)-46*(Wertl%L=0))
92 PRINT @(Ypointer%L,Xpointer%L-1);CHR$(-42*(Wert2%L=l)-46*(Wert2%L=0))
93 PRINT @(Ypointer%L-l,Xpointer%L);CHR$(-42*(Wert3%L=l)-46*(Wert3%L=0))
94 PRINT @(Ypointer%L-l,Xpointer%L-l);CHR$(-42*(Wert4%L=l)-46*(Wert4%L=0))
95 NEXT K%L
96 NEXT J%L
97 NEXT I%L
98 WEND
99 RETURN
Einfache CAM in OMIKRON.BASIC