
GEORG - Geiers Echt Optimale RasterGrafik
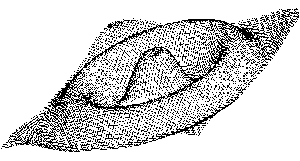
Wer sagt eigentlich, daß ein Programm,das dreidimensionale, bewegte Graphik erzeugt, immer aus endlosen Listings bestehen muß? Das hier vorgestellte Programm benötigt genau 53 Zeilen Quelltext, um die Oberfläche eines quadratischen Wasserbeckens darzustellen, in das gerade ein Tropfen gefallen ist. Es berechnet dazu 23 Einzelbilder, die danach fließend hintereinander dargestellt werden.
Das kann ein paar Minuten dauern. Durch bewußt kompaktierende Programmierweise ließen sich dabei sogar noch einige Zeilen einsparen (z.B., indem man die vier DIM-Anweisungen im ersten Teil zu einer zusammenfaßt etc).
Nach etwas Initialisierungskram werden aus der momentanen Bildschirmauflösung zwei Faktoren Fx% und Fy% gewonnen, durch die alle X- bzw. Y-Koordinaten geteilt werden müssen, um der jeweiligen Auflösung gerecht zu werden.
Sodann werden die X-Koordinaten der 6400 (80x80) betrachteten Punkte berechnet. Dies braucht nur einmal zu geschehen, da diese konstant sind. Schließlich kommt der eigentliche Zeichenalgorithmus. Gezeichnet wird ein Cosinus des Abstandes vom Ursprung (in der Mitte des Quadrats), umso stärker gedämpft, je größer dieser Abstand ist. Der Cosinus ist dabei um einen konstanten Phasenwinkel verschoben. Dieser ist nPi/11.5, wobei n die Nummer des gerade gezeichneten Bildes ist. Nach 23 Bildern ist der Winkel = 23Pi/11.5 = 2*Pi, also quasi wieder gleich Null.
An dieser Stelle bieten sich eine Menge Möglichkeiten, das Programm zu variieren. Beispielsweise könnte man die Dämpfung quadratisch zum Abstand verlaufen lassen, indem man statt A=Sqr... schreibt A=I+Sqr... und in der nächsten Zeile das F=(57-A)Cos... durch F=57/ACos... ersetzt. Auch völlig andere Funktionen (sin statt cos etc) können hier eingegeben werden. In diesem Zusammenhang ist es vielleicht wichtig zu wissen, daß die Werte für x1% und y1% im Intervall [-40;40] liegen und daß die Funktionsmaxima im Bereich [~-30-,-70] liegen sollten, da sonst die Ausgabe angepaßt werden muß.
Zur Ausgabe ist zu sagen, daß hier ein echter Hidden-Line Algorithmus Veirwendung findet, was bedeutet, daß GANZE Linien entweder gezeichnet oder weggelassen werden. Dies ist zwar nicht perfekt, da keine Linien angeschnitten werden, jedoch hält sich der Fehler in Grenzen, da die Linien sowieso nur eine durchschnittliche Länge von 5-6 Pixeln haben. Alles andere wäre (für meine Begriffe) zu langsam gewesen.
Der Algorithmus selbst ist, verhältnismäßig einfach: von jedem gezeichneten Anfangspunkt einer Linie wird die Höhe abgespeichert. Liegt ein neu zu zeichnen der Punkt unterhalb eines anderen, bereit in dieser Spalte gezeichneten, so ist er unsichtbar (Hierbei nutze ich aus, daß die Ebene von "vorn" nach" hinten" gezeichnet wird).
Schließlich werden die 23 so gewonnenen Bilder in rascher Abfolge hintereinander in den Bildschirmpeicher kopiert. Auch hier könnten noch einige Verbesserungen eingebaut werden. Beispielsweise könnte man sich die Kopiererei mit Sput sparen und stattdessen die Anfangsadresse des physikalischen Bildschirmspeichers mit Xbios (5,L:1,L:Varptr(C$(Z%)),-1) auf die abgespeicherten Bildschirme legen oder etwa die Zeiten zwischen den Bildwechseln variabel machen (Zeitlupe etc). Der Phantasie des Programmierers sind also keine Grenzen gesetzt, Die kompilierte Version brauchte bei mir 10:12 Minuten, also weniger als 25 Sekunden pro Bild. Dies läßt sich wohl auch noch verbessern, indem man beispielsweise die beiden Print Anweisungen wegläßt, oder für Feine Integervariable verwendet.
Wein es Spaß macht, der kann die Bilder auch gerne vorher abspeichern, um sich bei späteren Läufen des Programms die Rechenzeit zu ersparen. Dies wurde allerdings dem Zweck des Programms diametral entgegenlaufen. Ziel war es schließlich, den gewünschten Effekt mit einem möglichst KURZEN Programm zu erreichen. Wenn dieses kurze Programm jedoch erst 750K Daten laden muß, ist der Effekt verschwunden.
' (c) MAXON Computer GmbH 1989
'
DIM c$(22) ! Um Bilder abzuspeichern
cf=PI/11.5 ! Macht bei 23 Bildern =2*pi=1 Vollkreis
HIDEM ! Die hält nur auf (und stört die Graphik)
r%=XBIOS(4) ! Abfrage der Auflösung
fx%=1-(r%=0) ! Faktor für x-Umwandlung
fy%=1-(r%<2) ! Faktor für y- "
max_x%=640/fx% ! Bildschirmbreite
max_y%=400/fy% ! Bildschirmhöhe
DIM my%(max_x%) ! Für Hidden-Line-Algoritmus
DIM x%(80,80) ! Die X-Koordinaten...
DIM y%(80,80) ! ...und die Y-Koordinaten für die 6400 (80*80) Punkte
' -----------------------------------------------------------------------------
FOR x%=0 TO 80 !
FOR y%=0 TO 80 !
x%(x%,y%)=(20+x%*5+y%*3)/fx% !
IF x%(x%,y%)>max_x% ! Berechnung der realen
x%(x%,y%)=max_x% ! X-Koordinaten (konstant!!)
ENDIF !
NEXT y% !
NEXT x% !
' -----------------------------------------------------------------------------
FOR c%=0 TO 22 ! Dreiundzwanzig Bilder
PRINT 22-c% ! Ausdruck
cft=c%*cf ! Phasenwinkel
ARRAYFILL my%(),max_y% ! Für Hidden-Line
FOR x%=0 TO 80 ! Achzig Zeilen
FOR y%=0 TO 80 ! Achzig Spalten
x1%=x%-40 !\
y1%=y%-40 ! relatives Koordinatensystem
a=SQR(x1%*x1%+y1%*y1%) ! Abstand vom Ursprung...
f=(57-a)*COS(a/4-cft) ! ...dynamische Cosinusfunktion
y%(x%,y%)=(350-(y%*3+f))/fy% ! in Bildschirmkoordinaten.
NEXT y% ! nächste Spalte
PRINT AT(1,3);80-x%' ! Information
NEXT x% ! das wars schon
' ---------------------------------------------------------------------------
CLS
FOR y%=0 TO 79
FOR x%=0 TO 79
IF y%(x%,y%)<my%(x%(x%,y%)) ! Falls sichtbar..
DRAW x%(x%,y%),y%(x%,y%) TO x%(x%+1,y%),y%(x%+1,y%) TO x%(x%+1,y%+1),y%(x%+1,y%+1)
my%(x%(x%,y%))=y%(x%,y%)
ENDIF
NEXT x%
NEXT y%
SGET c$(c%)
NEXT c%
' -----------------------------------------------------------------------------
DO
FOR z%=0 TO 22
SPUT c$(z%)
NEXT z%
LOOP
Sven Geier