
Macromenia oder “Als Vip-Professional das Laufen lernte”
Wie der Titel schon sagt, werden wir unserem Vip-Professional heute gehörig Dampf machen und in die “Macrosprache” einsteigen. Vorab wiederum meinen besten Dank dem “vierundvierzigsten” Anrufer, der mich letzte Woche um 23.30h aus dem VIP-Schlaf gerissen und mir nahegelegt hat, etwas professioneller loszuschreiben. Doch vielleicht ist ihm die Einleitung im 1.Teil des Kurses noch nicht in die Hände gekommen, da stand nämlich “KURS für absolute Beginner”. Seien Sie mir deshalb nicht böse, wenn ich auf die ca. 85 % Anfänger Rücksicht nehme und etwas für die Basis schreibe. Vielleicht habe ich auch mal was für Semiprofis im Repertoire, die in den Teilen 5 fff. bestimmt nicht zu kurz kommen werden.
Den LOTUS-Anhängern, die mit 1-2-3 arbeiten und sich bei meinem Lektor Marcelo Merino ein klein wenig ausgesprochen haben, VIP sei nun mal nicht 1-2-3, denen sei bestätigt, daß ich genauso denke. Lotus 1-2-3 V1.A ist zwar identisch mit dem Befehls-, Formel-, und Syntaxaufbau, 1-2-3 ist jedoch um ein Vielfaches schneller (Textvip 8langsamer, Gemvip ca. 10langsamer) und auch leistungsfähiger, was die Speicherverwaltung anbelangt. (VIP schluckt fast 45 % mehr Speicherplatz)
1-2-3-Anwender, die mit der Version 2.01 arbeiten und dann im VIP schnuppern, werden sehr schnell bemerken, daß hier einiges fehlt.
VIP-Version 2.0?
Doch nun ein Aufruf an alle! Wäre es nicht schön, wenn VIP-Professional, angenähert an die LOTUS 1-2-3 Version 2.01 oder 3.0, auch für uns, den ehrgeizigen und ernsthaften Atari-Anwender, zu haben wäre? Vielleicht kann uns da die Firma Kiekbusch helfen, die ja einen sehr guten Draht zu den heutigen Supportern von VIP-Professional hat?
Zeigt her Eure Hausaufgaben
Bevor die verzweifelten "VIP-Schüler” die Hausaufgabe des letzten Teils noch kurz in der großen Pause vom Nebensitzer abpinseln, zeige ich ihnen im Anhang die Auflösung (Lösungslisting). Bauen Sie bitte Ihr Arbeitsblatt wieder so auf, daß wir alle von einem gemeinsamen Ausgangspunkt starten können. Unsere ersten Macrosequenzen werden speziell für diese Anwendung geschrieben. Doch zuvor sollte ich vielleicht erklären, was ein Macro in VIP-Professional ist.
MIDI, MINI, MACRO
Macros sind sequentiell, also nacheinander, ablaufende Befehlsfolgen, die nach einer Namensgebung in unserem VIP-Professional beliebige, zuvor festgelegte Tastenanschläge und/oder Befehle ausführen können. Das hört sich sehr kompliziert an, ist es aber überhaupt nicht.
Wir wollen unser Macroproblemchen mit einer etwas einfachen Anwendung angelten. Sie haben sicher alle bemerkt, daß beim Abspeichern und Laden unseres Arbeitsblattes auch die letzte Cursorposition abgespeichert wird. Stellen Sie den Cursor auf Zelle AA1 und geben Sie unsere Tastatursequenz zum Speichern des Arbeitsblattes ein: /, File, Save, (mit Return den Filenamen bestätigen), Replace.
Laden Sie das Arbeitsblatt wieder ein: /, File, Retrieve. Sie sehen, die Cursorposition ist mit dem gesamten Bildschirmaufbau an der Zelle AA1 orientiert. Dies kostet unnötig viel Bildschirmbewegung beim Rückladen der Anwendung und Rücksprung auf die Zelle A1.
Hätten wir nach dem Einladen der Anwendung die CLR-Home-Taste gedrückt, wäre der Bildschirm ideal aufgebaut. Mit etwas Raffinesse und VIP-Know-How können wir sogar ein Einfrieren von Spalten und Zeilen bewerkstelligen. Dieses Einfrieren erlaubt uns, später in der Anwendung zu marschieren, ohne die Zeilentitel und Spaltenüberschriften aus dem Blickfeld zu verlieren.

AUTOSTART-MACRO
Die eleganteste Lösung für unser Rückladeproblem ist der AUTOSTART-Macro mit dem Namen \0. Dieser Macroname wird bei jedem Rückladen einer Anwendung, in der dieser Macro gespeichert wurde, selbständig ausgeführt.
Wir wollen diesen Macro zunächst logisch aufbauen und nehmen dazu ein Blatt Papier zur Hand. Tun Sie mal so als würden Sie meine Fingeranschläge nach Abbildung 2 gemäß der Macrosyntax notieren.
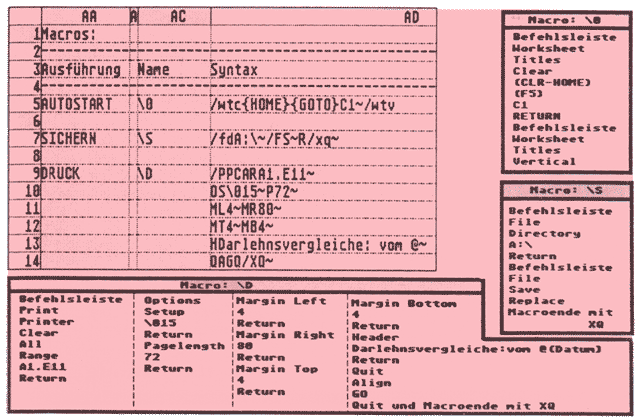
Alle Tastenanschläge erhalten ein Kürzel, das mit den Anfangsbuchstaben der Menüzeilen identisch ist, Funktions- und Sondertastenanschläge werden in spitze Klammern {} gesetzt und mit Klartext der Anweisung gefüllt. Ausnahmen gibt es hier auch, denn die Return-Taste muß mit dem Sonderzeichen ~ übergeben werden. Wie ich Sie bereits kenne, haben Sie fast alles verstanden und könnten Ihr Arbeitsblatt gemäß der Abbildung 3 aufbauen.
Bitte vergessen Sie nicht, die Zelleneintragungen AD5, AD7 und AD9 mit dem Sonderzeichen ‘ zu beginnen, denn VIP weiß ja nicht, ob Sie die Befehlsleiste rufen oder ein Macro generieren möchten.
Wenn alle Eintragungen erfolgreich abgeschlossen sind, positionieren Sie den Cursor auf Zelle AD5 und benennen Sie Ihren Macro mit der Taufprozedur: /, Range, Name, Create, \0, (Return), (Return) Bitte Cursor auf AD7, Taufglocken läuten: /, Range. Name, Create. \S, (Return), (Retum). Bei Zelle AD9 verwenden Sie nur den Namen \D. Bis hierher war es ja ganz einfach, doch die PD-Diskbesitzer Nr. 131 wissen, daß MACROS schnell und gefäääähhhrlich sind. Bitte speichern Sie Ihr Arbeitsblatt deshalb nach jeder Macrogenerierung ab. Sicherheitsfanatiker legen sich sogar noch eine Kopie Ihres Arbeitsblattes an. (Letzterem Aufruf sollten Sie bei der Arbeitsblattentwicklung Folge leisten).
Ich hab’s doch gewußt!
Schlauberger unter Ihnen werden die Taufsequenz zur Namensgebung selbstverständlich sofort in den Macro \C verwandeln. Hier die Lösung: /RNC{?}~~/ xq~ ( Befehlsleiste, Range, Name, Create, (Warten auf den Namen), Return, Retum, Ende des Macros).
MERLIN zückt den Macrozauberstab
Wer kennt Ihn nicht den großen Zauberer Merlin, der in der Sagenwelt lebt, und dem man Phantastisches nachsagen kann. Anscheinend hat er jetzt auch unserem VIP-Arbeitsblatt etwas Zauberpulver in die Zellen gestreut. Beim Rückladen unserer Anwendung passiert nämlich etwas Wundersames. Das Arbeitsblatt wird aufgebaut, der Cursor springt blitzschnell auf CI, und bewegen wir uns gen Osten, scheint der gesamte Westen (damit meine ich die Zeilenbeschriftungen) eingefroren zu sein. Niemand anderes als der Macro \0 ist an diesem Zauberstückchen schuld.
Das Abspeichem unseres Arbeitsblattes kann jetzt auch mit dem direkten Macroaufruf: TASTE ALT+S ausgeführt werden. Hat doch ganz prima geklappt! Nun noch unser Ausdruck (auf IBM-/EPSON-kompatiblen Druckern) mit dem Macroaufruf: TASTE ALT+D.
MEHR, MEHR MEHR...
habe ich 1983 gesagt, als Lotus 1-2-3 in unserem Unternehmen eingeführt wurde und ich nach 3-monatigem Handbuch-und Programmstudium (alles in Englisch) wegen Ernährungs- und Schlafmangel von meiner MS-DOS-Kiste weggezerrt wurde und zur Erholung einige Wochen Familie verordnet bekommen habe. Macros sind stark und vielfältig. Einmal dieser Macrosucht verfallen- und Sie kommen davon nicht mehr los. Haben Sie Ihr Arbeitsblatt einmal mit Macros ausgestattet, dürfen Sie es wie es die Profis tun, ab sofort Template nennen.
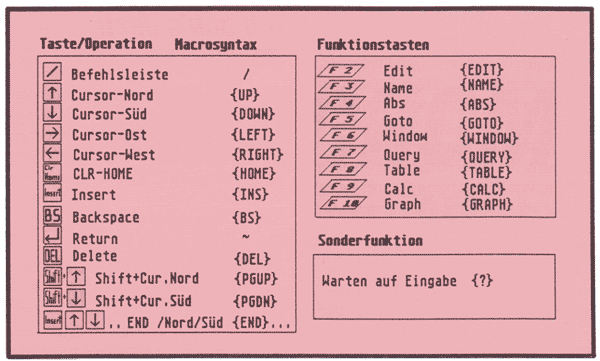
Damit es Ihnen leichter fällt, alle Tastatur- und Funktionstastenanschläge im Macrofieber auch in Ihre Zellen zu kriegen, zeigt die Abbildung 4 zeigt eine vollständige Macroreferenzliste:
War das schon alles, lieber Merlin?
Denkste, jetzt geht’s erst richtig los! Die Befehlsleiste mit ihren Untermenüaufrufen ist ja wirklich eine tolle, wenn auch anfangs etwas verwirrende Angelegenheit. Wir wollen in unser Template eine ebenso elegante Menüsteuerung integrieren.
Bitte bauen Sie Ihr Arbeitsblatt nach Abbildung 5 auf:
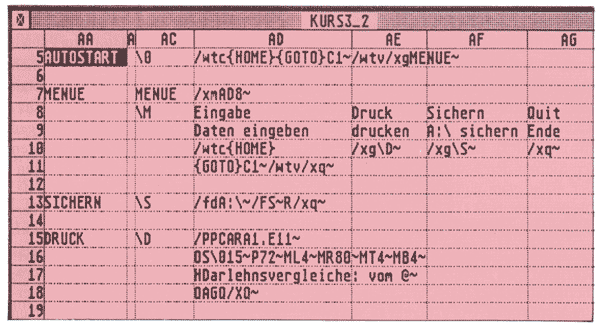
Mit unserem Taufmacro \C müssen wir wieder 2 Macronamen generieren bzw. benennen. Cursor auf AD6 stellen: /RNCMENUE~~ oder ALT+C (Taufmacro) und den Namen MENUE eingeben. Das gleiche nochmal: /RNC\M~~ oder ALT+C (Taufmacro) und Namen \M eingeben. Bitte das Sichern nicht vergessen und jetzt Augen zu, ALT+M gedrückt, staunen, wundem und sich freuen, unser erstes Menü ist fertig.
Menüs kann man nicht essen!
Aber elegant sind sie schon, nehmen eine Menge Tipperei ab und selbst mein 2-jähriger Sohn könnte das Darlehens-Template bedienen, wenn er nur schon lesen könnte.
In dem Menüaufbau traten erstmals die /x-Kommandos auf, die es ermöglicht haben, Sprungziele innerhalb eines Menüs zu gestalten, sowie eine Menüleiste in der VIP-Shell einzublenden. In Abbildung 6 erhalten Sie die Gesamtübersicht der /x-Kommandos.
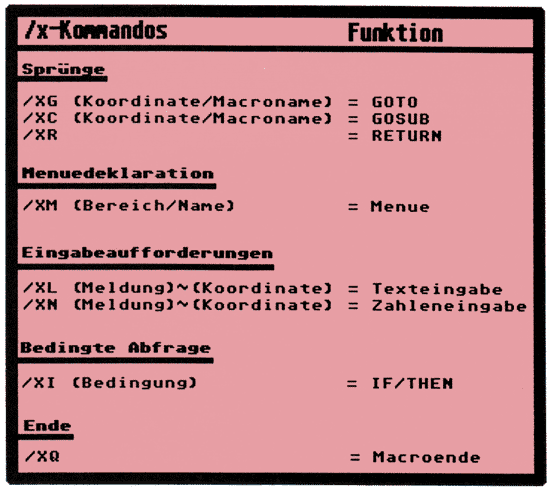
Do you speak VIP?
Ja, ab jetzt sprechen wir in einer anderen Sprache! Die nächtlichen Träume werden von den Basic-, Pascal- und C-Befehlen auf die Vip-Sprache abwandern. Man wird so manche Nacht mit einem Template zu kämpfen haben, um Macros einen sinnvollen Aufbau zu geben. Mit Erstaunen habe ich letzte Woche erfahren, daß alle neuen Mega-STs mit diesem phantastischen VIP-Professional ausgeliefert werden (ohne Aufpreis). Ich kann nur hoffen, daß man auch an die US-TEXT und US-GEM-Versionen gedacht hat, denn wie wir alle bereits festgestellt haben, werden die Macros innerhalb einer US-Shell nicht in der DEUTSCHEN-Shell lauffähig sein, geschweige denn wird mit der DEUTSCHEN-Shell eine Macrokompatibilität zu den großen Meistern Lotus 1-2-3 oder Symphony möglich sein.
| Operator | Operation | Reihenfolge |
|---|---|---|
| ^ | Potenzierung | 7 |
| -+ | negativ, positiv | 6 |
| */ | Multiplikation/Division | 5 |
| + - | Addition,Subtraktion | 4 |
| = <> | gleich, ungleich | 3 |
| <> | kleiner als, größer als | 3 |
| <= | kleiner als oder gleich | 3 |
| >= | größer als oder gleich | 3 |
| #NOT# | logisches NICHT | 2 |
| #AND# | logisches UND | 1 |
| #OR# | logisches ODER | 1 |
Abb. 7: Operatoren
Seltsamerweise (tut mir leid wenn ich mich wiederholen muß) ist im deutschen VIP (1.6) der Menüaufbau in deutsch, die Formeln und /X-Kommandos in englisch implementiert. Ein Versionsaustausch deutsch/englisch ist also mit Schwierigkeiten verbunden. Die universellste Version ist und bleibt die US-Shell 1.2- 1.4 GEM/TEXT. Nach meinen Informationen stellen die Kieckbusch-Mannen gegen UPDATE-Gebühr auch noch diese Version zur Verfügung. Eine weitere erfreuliche Nachricht kann ich allen “Sicherheitsfreundschaftskopienbesitzern” machen: Es gibt aus Überproduktionsbeständen für jedermann ein VIP-Professional Handbuch (50,- DM) zu kaufen. Es lohnt sich bestimmt ein solches Handbuch nachträglich zu erwerben. Wenn der didaktische Aufbau auch sehr an eine Direktübersetzung erinnert, erhalten Sie jedoch eine umfangreiche Übersicht aller Funktionen, Besonderheiten und Formeln. Den heißgemachten und SEMIs kann ich auch ein weiteres Nachschlagewerk empfehlen. Es ist zwar für Lotus 1-2-3 V 1. A geschrieben, diente mir aber im Anfangsstadium der Macromenia als sinnvolles Nachschlagewerk: “Das Lotus 1-2-3- Kompendium”, Verlag Markt und Technik, Autoren Geoffrey T. Le-Blond und Douglas Ford Cobb, übersetzt von Kurt Hinze und Dr. Horst Schmalfeld. ISBN:3-89090-005-4 (Preis ca. 58 — DM)
Ein VIP-FORUM?
Warum nicht, sprach Marcelo Merino, als wir über die vielen Briefe, Hilferufe und wirklich ernstzunehmenden Anrufe (43) diskutiert haben. Wir möchten alle VIPs gerne auffordern Ihre Lösungsvorschläge, Problemchen, Tips, Tricks und Kniffe allen VIP-Kämpfern zugänglich zu machen. Ihre Vorschläge und Problemlösungen werden, natürlich Ihr Einverständnis vorausgesetzt, in der ST veröffentlicht und besprochen. So könnten wir dem Bilanz- und Lohnbuchhalter, Vereinskassier, Versicherungsmakler, Zahnarzt, Hochschulprofessor und der Hausfrau helfen, ihre Anwendungen mit VIP zu erledigen.
Also greifen Sie zum Atari-Ferrari, schmeißen Sie das VIP-Template rein, merzen Sie alle Fehler aus, schreiben Sie eine kleine Erklärung dazu und schicken Sie das ganze an Merlin (nicht zu verwechseln mit dem Zauberer) oder direkt an mich, ich werde das Template durch den kritischen Testfilter meiner konstanten VIP-Viren jagen und dann nach Rücksprache gerne allen zur Verfügung stellen.
Rückblende und Versprechen
In Teil 2 habe ich versprochen, noch etwas aus dem Formelsprachschatz zu plaudern. Da VIP nun allen neuen MEGA-ST-Käufern zugänglich gemacht wird, kann ich auch ohne vorgehaltene Hand und böse Blicke der Atari- und Kiekbusch-Mannen noch etwas aus dem Formelsprachschatz rezitieren. Beginnen wir mit den OPERATOREN nach Abbildung 7.
Mit der Reihenfolgenummer wird die Reihenfolge angegeben, in der VIP Operationen in einer Formel ausführt. VIP führt die Operation mit .einer höheren Reihenfolgenummer vor einer Operation mit einer niedrigeren Reihenfolgenummer aus. Operationen mit derselben Reihenfolgenummer werden nacheinander von links nach rechts ausgeführt. Reihenfolgenummern können außer Kraft gesetzt werden, indem eine Operation in Klammern gesetzt wird. VIP führt Operationen in Klammern als erstes aus. Innerhalb der Klammerpaare gelten die Reihenfolgenummern. In einer Formel können bis zu 32 Klammerpaare benutzt werden.
Das folgende Beispiel in Abbildung 8 zeigt, wie VIP die Operationen nach Reihenfolgenummer ausführt:
478 + ((5800 + C8) * 0.1809) / 12 - C9
| | | | |
4 1 2 3 5
Abb. 8: Reihenfolgen
MATHEMATIK, oder das notwendige Übel!
Beispiele:
@ABS
berechnet den absoluten Wert einer Zahl oder eines Zelleninhalts:
@ABS(-8) = 8
@ABS(-789) = 789
@ABS(3) = 3
@EXP
berechnet den Wert der Konstanten “e” (angenähert am 2.7182818) mit dem Exponenten, der durch den Klammerausdruck bestimmt ist.
@EXP(5) = 148.41316
@EXP(C8) = 15.642632 (C8=2.75)
Falls die Zahl oder der Zelleninhalt größer als 230 ist, erscheint die Fehlemach-richt “ERR” (Error: englisch Fehler).
@INT
berechnet den ganzzahligen Anteil (INTEGER) der Zahl oder des Zelleninhalts.
@INT(8.987679) = 8
@INT($C$7) = 78 (wenn C7= 78.9878867 ist)
Zu beachten ist, daß @INT im Gegensatz zur @ROUND-Funktion einfach alle Dezimalstellen abschneidet.
@LN
berechnet den natürlichen Logarithmus (zur Basis “e”) der Zahl oder des Zelleninhalts.
@LN(17.634) =2.8698289
Die Zahl oder der Zelleninhalt müssen positiv sein, sonst erscheint die Fehlermeldung “ERR”. Bitte beachten Sie, daß die @LN-Funktion die Umkehrfunktion von @EXP ist.
@LOG
berechnet den Logarithmus (zur Basis 10) oder des Zelleninhalts.
@LOG(4.56) = 0.658964
@LOG(AB2) = 0.550839,
@SQRT
berechnet die Quadratwurzel der Zahl oder des Zelleninhalts.
@SQRT(5) = 2.236067
@SQRT(Z1) = 4, wenn Z1=16 ist.
@RAND
Die eingebaute @RAND-Funktion erzeugt Zufallszahlen zwischen 0 und 1 mit bis zu acht Dezimalstellen. Wenn Sie diese Funktion in eine Zelle eingeben, wird diese Zelle jedesmal einen anderen Wert zwischen 0 und 1 anzeigen, wenn die Tabelle neu berechnet wird.
@ROUND
Die @ROUND-Funktion wird benutzt, um Zahlen auf eine bestimmte Genauigkeit zu runden. Das allgemeine Format dieser Funktion ist:
@ROUND(ZAHL,DEZIMALSTELLEN)
Die Dezimalstellen können einen Wert zwischen 15 und -15 interpretieren und die Stellen rechts beziehungsweise links vom Dezimalpunkt wiedergeben.
@ROUND( 19.98789,2) = 19.99
@ROUND( 123.453,-2) = 100
@ROUND( 123.456,-1) = 120
Der entscheidende Vorteil der @ROUND-Funktion ist, daß Sie den Rundungsfehler bei Geldbeträgen verringern. In unserer Darlehensanwendung ließe sich somit die 3. Nachkommastelle eliminieren.
@MOD
Die @MOD- Funktion zeigt den Rest einer Division an. Das allgemeine Format ist (Modulo-Rechnung).
@MOD(Divident,Divisor)
@MOD(7,3) = 1 (7:3 = 2 Rest 1)
@MOD(71.3,21) = 8.3 (71,3:21=3 Rest 8.3)
Eine Nulldivison wird mit Fehlermeldung ERR ausgegeben.
| Funktion | Kurzbeschreibung |
|---|---|
| @ABS | absoluter Wert einer Zahl |
| @EXP | Wert der Konstante "e" |
| @INT | ganzzahliger Anteil |
| @LN | natürlicher Logarithmus ,,e,‘ |
| @LOG | Logarithmus Basis 10 |
| @SQRT | Quadratwurzel |
| @RAND | Zufallszah1 |
| @ROUND | Rundungen mit Nachkommastellen |
| @MOD | Anzeige: Rest einer Division |
Abb. 9: Mathematik
GEOMETRIE, Laster und Leiden!
VIP besitzt auch einen vollständigen Satz trigonometrischer Funktionen, die ich als Schüler immer verabscheut habe und bei denen ich nur durch Abschreiben bei meinen Mitschülern brillieren konnte. (Hoffentlich bekommt keiner meiner ehemaligen Professoren diesen Bericht in die Hände)
Viele VIP-Benutzer werden diese Funktionen sicherlich nie anwenden. Aber diejenigen, die VIP zum Lösen von Ingenieuraufgaben einsetzen, werden diese Funktionen nach Abbildung 10 nützlich finden.
@PI
gibt die Zahl PI(3.141592653589794) zurück. PI ist die Verhältniszahl eines Kreisumfangs zum Durchmesser.
@SIN(30*@PI/180) = 0.5
@PI*4^2 = 50.26548,
der Inhalt eines Kreises Radius 4
@SIN
gibt den Sinus einer Zahl oder Zellenadresse zurück. Der Winkel (ZAHL) muß als Radiant ausgedrückt sein.
@SIN(@PI/6) = 0.5
@SIN(90*@PI/180) = 1
@SIN(30*@PI/180) = 0.5
@cos
gibt den Cosinus von Winkel x 1 zurück. Das Ergebnis liegt zwischen -1 und 1 einschließlich. Der Winkel x muß als Radiant ausgedrückt werden.
@COS(60*@PI/180) = 0.5
@TAN
gibt den Tangens von Winkel x zurück. Der Winkel x muß in Radiant ausgedrückt werden.
@TAN(30*@PI/180) = 0.5
@ASTN
berechnet den Arkussinus eines Winkels. Diese Funktion gibt den Winkel als Radiant zurück, dessen Sinus gleich x ist. Das Ergebnis liegt stets zwischen -PI/1 und PI/2 und stellt einen Winkel im I. oder II.Quadranten dar. Das Argument x muß zwischen -1 und 1 einschließlich liegen.
@ASIN(-0.264) = -0.24855 (Radiant)
@ASIN(WINKEL) = 0.523598 (Radiant),
wenn die Zelle namens WINKEL den Wert 0.5 enthält.
@ACOS
berechnet den Arkuscosinus eines Winkels. Diese Funktion gibt den Winkel als Radiant zurück, dessen Cosinus gleich x1 ist. Das Ergebnis liegt stets zwischen 0 und PI und stellt den Winkel im I. oder II. Quadranten dar. Das Argument x muß zwischen -1 und 1 einschließlich liegen.
@ACOS(-0.3) = 1.875488 (Radiant)
@ATAN
berechnet den Arkustangens im III. Quadranten eines Winkels. Der Winkel, dessen Tangens ZAHL ist, wird als Radiant zurückgegeben. Das Ergebnis liegt stets zwischen -PI/2 und PI/2 und stellt einen Winkel im I. oder IV. Quadranten dar. Für den Wert des Arguments x gibt es keine Einschränkungen.
@ATAN(1) = 0.785398 (Radiant)
| Funktion | Kurzbeschreibung |
|---|---|
| @PI | Konstante PI (3.141592653589.3) |
| @SIN | Sinusfunktion |
| @COS | Cosinusfunktion |
| @TAN | Tangensfunktion |
| @ASIN | Arkussinus |
| @ACOS | Arkusc os i nus |
| @ATAN | Arkustangens |
Abb. 10: Geometrie
Finanzmathematische Funktionen oder der Weg zum Geld!
@IRR
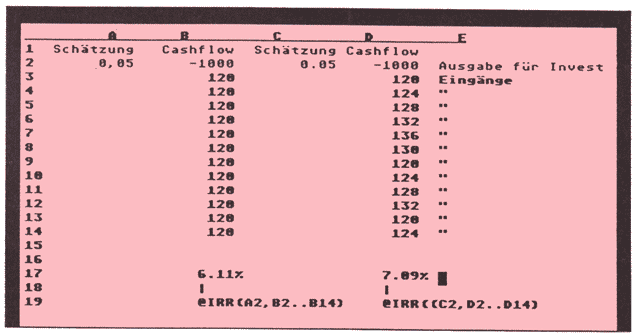
berechnet die interne Ertragsrate für eine Reihe von Cashflow-Werten, die sich aus einer Investition ergeben. Im allgemeinen handelt es sich bei @IRR um die Raten, die dem aktuellen Wert einer erwarteten künftigen Folge von geraden oder ungeraden Cashflows für die ursprüngliche Investition entspricht. VIP geht davon aus, daß der Cashflow in regelmäßigen Abständen eingeht. Mein Beispiel sehen Sie in Abbildung 12. Meine beiden Beispiele in dieser Tabelle zeigen zwei Arten der Anwendungsmöglichkeit von der@IRR-Funktion.
a.)@IRR(A2,B2..B 14) gibt 6,11 % über eine 12-monatige Laufzeit zurück, wenn sich die erste Investition/ Zahlung auf DM 1000,— und die zwölf periodischen Eingänge auf jeweils DM 120,— belaufen. In Bereich B1..B13 enthält Bl den Wert 1000,— und B2..B13 enthalten jeweils den Wert 120,-.
b.)@IRR(C2,D2..D14) gibt 7,09 % über eine 12-monatige Laufzeit zurück. wenn sich die erste Investition/ Zahlung auf DM 1000,- und die zwölf monatlichen Einträge auf folgende Summen belaufen: 120, 124, 128, 132, 136, 130, 120, 124, 128 , 132, 120, 124.
| Funktion | Kurzbeschreibung |
|---|---|
| @IRR | Interner Zinsfuß |
| @NPV | Barwertsberechnung |
| @FV | Endwert einer Annuität |
| @PV | Barwert einer Annuität |
| @PMT | gleichbleibende Rückzahlungsraten pro Periode für ein Dar1ehn |
Abb. 11: Finanzmathematik
@NPV
berechnet den aktuellen Wert einer Reihe künftiger Cashflows. VIP geht davon aus, daß der periodische Zinssatz fest ist, und daß die Reihe von Cashflows (Zahlungsrückfluß) in gleichen Zeitintervallen stattfinden. Der erste Barabgang wird für das Ende der ersten Periode angenommen. Nachfolgende Cashflows finden am Ende der folgenden Perioden statt.
@NPV(ZINSSATZ,CASHFLOW-BEREICH)
Zinssatz ist der periodische Zinssatz. Cashflow-Bereich ist der Bereichsname oder die Adresse, die zur Speicherung der Serie mit Cashflows benutzt wird. @NPV benutzt folgende Formel:
(1 +Zinssatz)‘
wobei:
Vi .. Vn = Folge von Cashflows in Cashflow-Bereich
Zinssatz = Zinssatz
n = Anzahl von Cashflows
i = laufende Wiederholung (1 bis n)
Um den aktuellen Nettowert einer Investition zu ermitteln, bei der es sofort zu einem Barabgang kommt, auf den eine Reihe künftiger Bareingänge folgen, muß der ursprüngliche Abgang separat faktorisiert werden, da er von dem Zinssatz nicht betroffen ist.
Ist ANFANG der erste Barabgang, SERIE ein Bereich mit zukünftigen Cashflows und Zinssatz der periodische Zinssatz, so wird der gesamte aktuelle Nettowert folgendermaßen angegeben:
+ Anfang + @NPV (ZINSSATZ, SERIE)
@PV
die @PV-Funktion findet für die Berechnung des Barwertes einer Annuität Anwendung, dargestellt durch RATE, ZINSSATZ und ANZAHL der PERIODEN. Eine Annuität besteht aus einer Reihe von gleichen Raten, die in konstanten Zeitabständen gezahlt werden. Der Barwert ist der jetzige Wert aller Zahlungen, die später getätigt und um einen bestimmten Zinssatz diskontiert werden. Die Berechnung des Barwertes einer Annuität erlaubt Ihnen, verschiedene Investitionsmöglichkeiten oder potentielle Verpflichtungen hinsichtlich des Geldwertes miteinander zu vergleichen.
Das allgemeine Format der @ PV-Funktion lautet:
@PV(RATE, ZINSSATZ, PERIODENZAHL)
Die allgemeine Formel zur Berechnung der Annuität heißt:
PV = Rate * ((1 - (1+Zinssatz)n)/Zinssatz)
In unserem Arbeitsblatt (Abbildung 13) wird die Formel folgendermaßen verwendet.
Der Unterschied zwischen der @NPV-Funktion und der @PV-Funktion beruht auf den Unterschieden bei den Zahlungsströmen und der Art, wie diese in der Tabelle angezeigt werden. @NPV berechnet den Barwert aus einer Zahlungsreihe, die gleiche und ungleiche Werte enthalten kann, die aber alle einem Zellenbereich in der Tabelle angehören. Die Raten in der@PV-Funktion müssen alle gleich sein, und dieser Betrag muß in einer einzigen Zelle stehen oder als Wert in die @PV-Formel eingegeben werden.

@FV
diese Funktion entspricht in Ihrer Form der @PV-Funktion, wird aber zur Berechnung des Endwertes einer Annuität benutzt. Der Endwert ist der Wert einer Reihe von Ein- oder Auszahlungen zu einem zukünftigen Zeitpunkt, aufgezinst mit einem bestimmten Zinssatz. Die Berechnung des Endwertes einer Zahlungsreihe erlaubt Ihnen, verschiedene Investitionsaltemativen oder potentielle Verpflichtungen miteinander zu vergleichen.
Das allgemeine Format der @ FV-Funktion lautet:
@FV(RATE, ZINSSATZ, PERIODENANZAHL)
Die Formel zur Berechnung des Endwertes einer Annuität ist:
FV = ((1+ZINSSATZ)n-1)/ZINSSATZ
@PMT
berechnet die periodische Zahlung eines Darlehens. Die meisten Abzahlungskredite werden wie Annuitäten einer nachschüssigen Rente berechnet, d.h. die Zahlungen werden am Ende jeder Zahlungsperiode vorgenommen.
KAPITAL entspricht dem Darlehensbetrag.
ZINSSATZ entspricht dem periodischen Zinssatz
PERIODEN entspricht der Anzahl der Zahlungsperioden
@PMT benutzt folgende Formel zur Berechnung der periodischen Zahlungen:
KAPITAL * (ZINSSATZ / (ZINSSATZ+1))
wobei:
KAPITAL = Kapital
ZINSSATZ = Zinssatz
n = Perioden
Nehmen wir einmal an, bei Ihnen ist der Geldregen ausgebrochen und Sie entschließen sich eine Eigentumswohnung für 250.000,-DM zu kaufen. Die Finanzierung splittet sich in 2 Hypotheken zu DM 150000,— und DM 100000,—. Die Laufzeit beträgt im 1. Fall 30 Jahre, im 2.Fall 25 Jahre.
Für die Hypotheken erstellen wir folgende Formel:
@PMT(150000,6.75%/12,30*12) = DM 972.89
@PMT(100000,6.75%/12,25*12) = DM 690.91
Gesamtbelastung somit DM 972,89+DM 690.91 = DM 1663.80 pro Monat
Mach mal Pause!
“Kann ich nie, lerne ich auch nicht, kann ich nicht gebrauchen !” Ich höre es ja, Sie brauchen nicht auf mich loszuwettern. Es ist eben sehr umfangreich, dieses VIP-Professional, stellen Sie sich mal vor, es gibt auch noch den Teil Datenbank und Grafik, der ebenfalls behandelt werden möchte. Sie haben richtig gehört, unsere bis jetzt behandelten Formeln, Macros und Funkionen betreffen nur den Kalkulationsteil. Au weh ! Hoffentlich springen mir nicht die Leser ab, wenn ich Sie mit dem gesamten Sprachschatz konfrontiere.
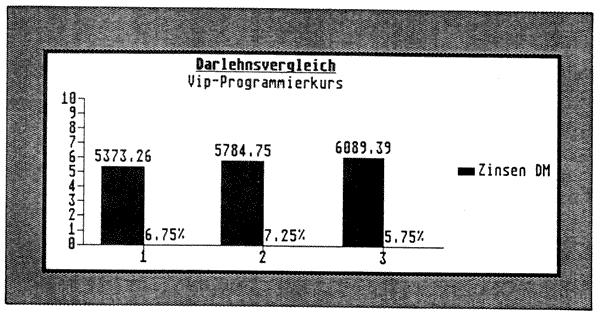
Walk on the wild Side
würde LOU REED sagen, wenn ich ihm wieder eine Hausaufgabe geben müßte. Aber ich werde Sie diesmal verschonen. Bitte schauen Sie sich nachfolgende Grafik an. Wie man so etwas macht, lernen Sie im nächsten Teil.
Bei Problemen:
Heini D. Schultz
Ingersheimer Strasse 12
7140 Ludwigsburg