
Fractals: Reise Ins Chaos
Wer hat sie noch nicht gehört, die Begriffe wie Mandelbrot-Menge, Julia-Menge oder Apfelmännchen? Hinter diesen Begriffen steckt der Reiz des Unendlichen, die Faszination skurriler Gebilde. Wohl jeder, der Fractals erblickt hat, ist von ihnen beeindruckt.
Legen Sie den Artikel nicht gleich weg, wenn Sie jetzt zuerst etwas über Mathematik lesen. Die mathematische Grundlage für unsere Fractals ist überaus einfach.
Das Reizvolle an einem Fractal ist seine Eigenschaft, fraktal zu sein. Fraktal heißt ein Gebilde, um es rocken auszudrücken, wenn es selbstähnlich ist, und wenn der Rand unendlich zerklüftet ist. Mit anderen Worten heißt dieses, daß man jedes Gebilde oder Teilgebilde an beliebigen Stellen unendlich oft wiederfindet, jedesmal noch schöner und reizvoller. An keinem Stück des Randes wird man ein glattes Stück finden, immer ergeben sich neue Randformen. Es sieht chaotisch und geordnet zugleich aus. Gerade diese beiden Eigenschaften machen der Reiz der Fractals aus!
Hinter den Begriffen Mandelbrot-Menge, Julia-Menge und Apfelmännchen steckt ein und dieselbe Formel. Fangen wir mit der Geschichte an. Die Mandelbrot-Menge wurde nach Benoit B. Mandelbrot, einem aus Polen stammenden Mathematiker, benannt. Gefunden wurde sie erst im Jahre 1980. Seitdem wird ununterbrochen nach weiteren Ablegern gesucht, hier bei uns etwa von einer Bremer Forschungsgruppe. Diese Forschungsgruppe gab den Mandelbrot-Mengen einen Spitznamen: Apfelmännchen. Der Rand der Mandelbrot-Menge hat wieder einen besonderen Namen: Julia-Menge. Die Julia-Mengen, die ihren Namen em französischen Mathematiker Gaston Julia verdanken, haben einen zum Apfelmännchen analogen Aufbau, mit einer klitzekleinen Veränderung. Zu dieser Veränderung kommen wir später.
Ein Apfelmännchen ist ein ebenes Gebilde. Die Ebene, auf der es entsteht, heißt Zahlenebene oder komplexe Zahlenebene. Im Gegensatz zu den schon meist aus der Schule bekannten reellen Zahlen, die auf einer Zahlengeraden dargestellt werden, werden diese Zahlen in der Ebene dargestellt.
Neben der waagerechten Komponente, dem Realteil, hat eine komplexe Zahl noch eine senkrechte Komponente, den Imaginärteil. Um die Zahl leichter darstellen zu können, teilt man sie in die beiden Komponenten auf: z = (a,b). Die komplexe Zahl z hat den Realteil a und den Imaginärteil b. Diese Darstellung ist ähnlich einer gewöhnlichen Ebenendarstellung. Es gibt aber noch eine zweite Schreibweise: z = a+ib. Die Zahl i hat die ganz besondere Eigenschaft i2 = -1, sie ist also die Quadratwurzel aus -1! Im Bild 1 ist eine graphische Darstellung der komplexen Zahlen zu sehen.
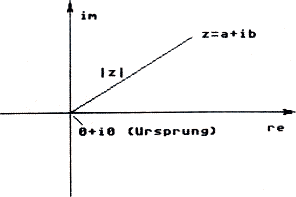
Jetzt, wo wir die komplexen Zahlen kennengelernt haben, merken wir schon, daß man wohl gewohnt addieren und subtrahieren, nicht jedoch multiplizieren und dividieren kann.
Es wird eine neue Multiplikation eingeführt:
yz = ac-bd+i(ad+bc),
wobei y = a+ib, z = c+id komplexe Zahlen sind.
Ein Beispiel:
(5+3i)*(-3+4i) = 5*(-3)-3*4+i* (5*4+3*(-3)) = -27+11i
Eine Division direkt ist nicht möglich. Dazu wird das komplex Konjugierte der komplexen Zahl benötigt. Da wir die Division zweier komplexer Zahlen für unsere Betrachtungen nicht brauchen, wird hier nicht weiter darauf eingegangen.
Der Betrag einer komplexen Zahl z=a+ib berechnet sich folgendermaßen: |z| = (a2+b2)0,5. Der Betrag ist anschaulich gesehen die Länge der Strecke vom Ebenen-Ursprung zur Zahl a+ib.
Bevor wir nun wieder auf die Apfelmännchen zurückkommen, brauchen wir noch ein wenig Mathematik. Eine Folge von Zahlen entsteht mit Hilfe einer bestimmten Vorschrift, einer Iterationsvorschrift. Hierbei können Zahlen als Folgenglieder unter Benutzung einer festen Vorschrift entstehen, die von nichts weiter abhängt, als von der zugrundegelegten Zahl. Die Folge der Stammbrüche (Berechnungsformel 1/n, n ist eine natürliche Zahl, also 1, 2, 3, ...) ist eine solche Folge. Es entstehen hier die Zahlen 1, 1/2, 1/3, .... Bei solchen Folgen kann man relativ leicht Vorhersagen, ob sie sich einer festen Zahl beliebig nähern, man spricht von “konvergieren”, oder eben nicht, was mit “divergieren” bezeichnet wird.
Eine andere Art von Folgen entsteht, wenn vorige Folgenglieder benutzt werden, um ein neues zu bestimmen. Diese Folgen heißen rekursive Folgen. Und gerade dieser Typ von Folgen liegt unseren Apfelmännchen zugrunde. Es wird eine Zahl vorgegeben und die nächste wird aus der vorherigen berechnet, indem man sie quadriert und eine Konstante addiert:
zn+1=zn2+c
Das einzige Problem hierbei ist, daß unsere Zahlen komplex sind und wir die komplexe Multiplikation und Addition bemühen müssen. Nehmen wir einmal an, zn sei gleich x+iy und c sei a+ib. Dann berechnet sich der Realteil des neuen Folgengliedes als xx-yy+a und der Imaginärteil als 2xy+b. Diese Formel werden wir benutzen, um die Apfelmännchen zu berechnen.
An dieser Stelle ist der mathematische Exkurs beendet, wir gehen zur Umsetzung in ein Programm über. Es soll hier allerdings kein vollständiges Programm dargelegt werden, sondern nur einzelne Routinen, die man selbst zusammenfassen kann.
Welche komplexen Zahlen sind überhaupt passend? Grob gesagt, alle um den Ursprung in der komplexen Zahlenebene. Genauer ausgedrückt sollte der Realteil und der Imaginärteil jeweils etwa zwischen -2 und 2 liegen. Neben den Koordinaten aus der komplexen Zahlenebene werden natürlich auch noch Bildschirmkoordinaten gebraucht. Diese Koordinaten beziehen sich auf unsere Pixel. Gleichzeitig muß man also mit zwei verschiedenen Koordinatenpaaren rechnen.
Um es einmal graphisch zu veranschaulichen, betrachten wir Bild 2, wo ein kleines Übertragungsbeispiel zu erkennen ist.
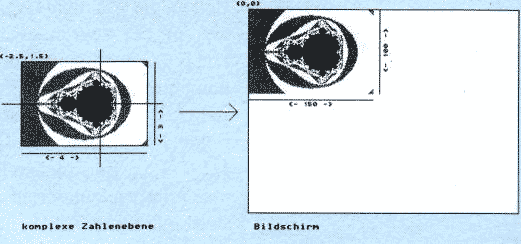
Die Beispiele sind übrigens in GFA-Basic geschrieben, allerdings sind die Routinen so allgemein gehalten, daß man auch jede andere Programmiersprache verwenden kann. Geschwindigkeit ist jedoch Trumpf, da für ein Bild viele tausend Berechnungen durchgeführt werden müssen, was bei ausreichender Rechengenauigkeit mitunter Stunden dauern kann.
Die in eine Prozedur umgesetzte Koordinatenberechnung ist im Listing 1 zu finden.
Der Prozedur FRACTAL werden folgende Werte übergeben:
x% : die x-Koordinate der oberen linken Bildecke auf dem Bildschirm
y% : die y-Koordinate dazu
w%: die Breite des Bildes auf dem Bildschirm
h%: die Höhe dazu
xk: die x-Koordinate der oberen linken Ecke eines Ausschnittes auf der komplexen Zahlenebene
yk: die dazugehörige y-Koordinate
wk: die Breite des Ausschnittes auf der komplexen Zahlenebene
hk : die Höhe dazu
Max_iter% : Obergrenze für die Iteration
A,B: Konstanten
V_... : variierende Werte
Die Iteration kann natürlich nicht unbeschränkt ausgeführt werden, daher beschränken wir uns auf dem Rechner auf höchstens Max_iter% Werte und schätzen dann die Konvergenz ab: Wird Max_iter% erreicht, ohne daß die Folgenglieder eine bestimmte Schranke überschreiten, nehmen wir an, daß die Folge mit den vorgegebenen Startwerten konvergent ist, sonst eben divergent.
Da bei Divergenz die magische Obergrenze Max_iter% nicht erreicht wird, findet diese Abbruchzahl auch noch Verwendung. Das sehen wir allerdings erst später.
Die beiden angesprochenen Prozeduren MANDELBROT und JULIA enthalten die eigentliche Konvergenzbestimmung. Beide Prozeduren sind recht ähnlich, und doch unterscheiden sie sich.
Für die altbekannte Mandelbrotmenge wird der z-Wert konstant gehalten. Hier bringen zwar unterschiedliche Konstanten auch unterschiedliche Graphiken, der Unterschied ist aber nicht so berauschend wie bei den Julia-Mengen. Eine Veränderung der Konstanten lohnt sich also nur für die Julia-Mengen. Konstant gehalten werden natürlich nur die Startwerte! Die Iteration, getrennt nach Real- und Imaginärteil, befindet sich in der While-Schleife.
Die Prozeduren MANDEFBROT und JULIA sind in den Listing 2 und 3 aufgeführt.
Die Variablen, die mit Z_ beginnen, sind die z-Werte aus der Iterationsvorschrift, die mit C_ die c-Werte. “re” steht für Real-Teil und “im” für Imaginärteil.
Der Grundalgorithmus läßt sich in dem in Bild 3 zu sehenden Struktogramm darstellen.
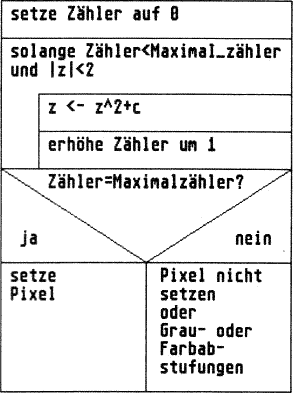
Der jeweils resultierende Wert für Zähler ist für die Pixel ausgabe wich-ng. Eine einfache Umsetzung könnte so erfolgen:
Setze Pixel,
falls Zaehler%>=Max_iter%,
sonst nicht.
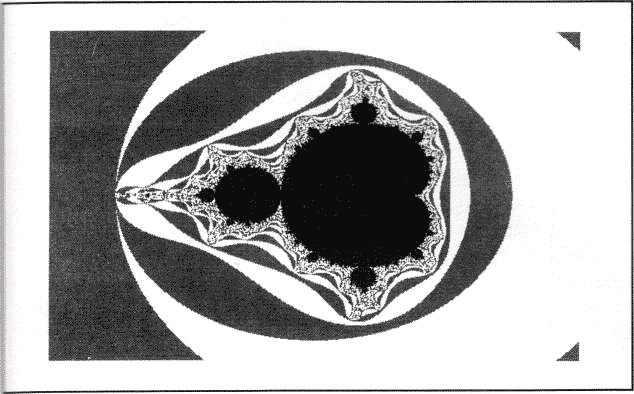
Wer allerdings eine schönere Ausgabe wünscht, der bezieht noch die Punkte der Divergenz mit ein. Erst durch diese Punkte ergibt sich ein (fast) vollendetes Formen- und Farbenspiel. Beispielsweise können graue Bereiche eingeführt werden, wie es in dem Ausgabebeispiel der Fall ist. Ebenso könnte man aber auch je nach Wert die Pixel in einer anderen Farbe setzen. Es gilt aber nicht unbedingt, daß viele Farben auch ein besonders tolles Bild ergeben. Weniger ist oft mehr!
Eine Beispielausgabe ist im Listing 4 zu betrachten. Die vier vorgestellten Prozeduren kann man auch gut zu ziner relativ kompakten zusammenfassen, was auch der Geschwindigkeit zugute kommt. Eine Zusammenfassung für die Mandelbrot-Mengen ist im Listing 5 zu erkennen. Dieses Listing enthält im Gegensatz zu den anderen ein lauffähiges Programm! Bei welchen Koordinaten das "Grund”-Apfelmännchen zu finden ist, wurde schon angesprochen. Besonders schöne Ableger gibt’s beispielsweise an den Stellen, wo zwei größere Teile des Apfelmännchens zusammenliegen. Auch kleine Flecke, die recht unscheinbar irgendwo liegen, sollte man nicht verachten, denn gerade dort könnte sich ja eine Selbstabbildung der Mandelbrot-Menge befinden.
Die kompaktere Fractal-Routine aus Listing 5 ist zum “Zoomen” geeignet, d.h. man kann sie gut benutzen, um Ausschnitte aus der Mandelbrot (oder Julia-) Menge zu vergrößern. Die Vergrößerungsmöglichkeit wird ja dringend benötigt, da unsere Monitore und auch unser Auge nur ein begrenztes Auflösungsvermögen haben. Den Rand zoomen wir uns heran, damit er klar genug wird. Als Koordinaten auf der reellen und der imaginären Achse beginnen wir mit etwa -2 und 2, also einem Bereich von 4. Bei starken Vergrößerungen kann es aber leicht passieren, daß man sich nur noch im Bereich von 0.01 oder noch weniger bewegt. Wenn man Pech hat, verliert man den Rand aus den Augen. Daher sollte man sich die Koordinaten der Bilder immer notieren (Koordinaten auf der reellen und der imaginären Achse, übergebene Konstanten und natürlich den Wert für die maximale Iterationsanzahl). Die Koordinaten könnten beispielsweise für die linke obere Ecke 0.7453444,0.1130534, für die Breite 0.0005516 und die Höhe 0.0000994 lauten. Die Konstanten sind einfach 0, gerechnet wird bis 400! Bei dieser Rechnung sollte man schon etwas Zeit mitbringen. Meine Empfehlung: Rechner abends anschalten und Programm starten und über Nacht laufen lassen.
Für Julia-Mengen wählt man ähnliche Koordinaten wie für die Mandelbrot-Mengen. Zusammenhängende Julia-Mengen erhält man, wenn man für den konstanten Wert c Werte aus dem Inneren der Mandelbrot-Menge wählt.
Wie weit soll die Iteration fortgeführt werden, um eine Aussage über die Konvergenz zu wagen? Diese Frage ist gamicht so leicht zu beantworten. Je kleiner der Ausschnitt ist, desto größer sollte man Max_iter% wählen. Das können ohne weiteres Werte von 100 und mehr sein. Für gröbere Ausschnitte kann man notfalls auch bis etwa 20 heruntergehen, wodurch aber der fraktale Rand schon leiden könnte.
Ist nun schon Schluß? Nein, jetzt geht’s erst richtig los. Fractals ergeben sich nicht nur mit der Iterationsvorschrift zn+1 = z2+c. Wie wäre es mit zn+1= zn3+c? Oder eine etwas kompliziertere Iteration zn+1=(z2+1)/zn (zn+12-1)? Eine Grenze fürs Experimentieren ist nicht gesetzt.
Nach diesem kleinen Ausflug in das Land der Fractals sind auch sicher Sie so begeistert, daß Sie sich Ihren Rechner schnappen und sich ein eigenes Fractal-Programm schreiben. Oder lesen Sie den Artikel schon nicht mehr und sitzen bereits am Rechner?
Dietmar Rabich
Literatur:
[1] Spektrum der Wissenschaft 2/88, Computer-Kurzweil, A. K. Dewdney
[2] The Beauty of Fractals, H.-O. Peitgen/ P. H. Richter, Springer-Verlag
[3] Computer grafische Experimente mit Pascal, K.-H. Becker! M. Dörfler, Vieweg-Verlag
'
' (c) MAXON Computer 1989
'
' Fractal: Koordinatenberechnung
PROCEDURE fractal(x%,y%,w%,h%,xk,yk,wk,hk,max_iter%,a,b)
LOCAL v_re_schritt,v_im_schritt ! Schrittweiten für
LOCAL i%,j% ! Pixelkoordinaten
'
v_re_schritt=wk/w% ! Schrittweite horizontal
v_im_schritt=-hk/h% ! Schrittweite vertikal
'
v_im=yk ! Startwert vertikal/oben
FOR j%=y% TO y%+h%
v_re=xk ! Startwert horizontal/links
FOR i%=x% TO x%+w%
GOSUB mandelbrot ! Iteration
GOSUB plot_pixel(i%,j%,zaehler%) ! Ausgabe
ADD v_re,v_re_schritt
NEXT i%
ADD v_im,v_im_schritt
NEXT j%
RETURN
Listing 1: Procedure Fractal
'
' (c) MAXON Computer 1989
'
' Fractal: Iteration Mandelbrot-Menge
PROCEDURE mandelbrot
LOCAL z_re_h
LOCAL z_re_m,z_im_m
LOCAL c_re_m,c_im_m
'
z_re_m=a ! z-Werte konstant
z_im_m=b
c_re_m=v_re ! c-Werte variabel
c_im_m=v_im
'
zaehler%=0
WHILE zaehler%<max_iter% AND z_re_m*z_re_m+z_im_m*z_im_m<4
z_re_h=z_re_m
z_re_m=z_re_m*z_re_m-z_im_m*z_im_m+c_re_m
z_im_m=2*z_re_h*z_im_m+c_im_m
INC zaehler%
WEND
RETURN
Listing 2: Iteration Mandelbrot-Menge
'
' (c) MAXON Computer 1989
'
' Fractal: Iteration Julia-Menge
PROCEDURE julia
LOCAL z_re_h
LOCAL z_re_m,z_im_m
LOCAL c_re_m,c_im_m
'
z_re_m=v_re ! z-Werte variabel
z_im_m=v_im
c_re_m=a ! c-Werte konstant
c_im_m=b
'
zaehler%=0
WHILE zaehler%<max_iter% AND z_re_m*z_re_m+z_im_m*z_im_m<4
z_re_h=z_re_m
z_re_m=z_re_m*z_re_m-z_im_m*z_im_m+c_re_m
z_im_m=2*z_re_h*z_im_m+c_im_m
INC zaehler%
WEND
RETURN

Listing 3: Iteration Julia-Menge
' Kompakter Fraktal-Generator
' (Entw. mit GFA-Basic.)
' D. Rabich, 2.2.1988
'
' (c) MAXON Computer 1989
'
GOSUB fractal(0,0,639,399,-2.5,1.5,4,3,75,0,0) ! zum Fractal-Generator
OPEN "O",#1,"FRACTAL.DOO" ! Bildausgabe
GET 0,0,639,399,bild$
PRINT #1,MID$(bild$,7);
CLOSE #1
END
'
' Fractal-Generator
PROCEDURE fractal(x%,y%,w%,h%,xk,yk,wk,hk,max_iter%,a,b)
LOCAL v_re_schritt,v_im_schritt ! Schrittweiten
LOCAL i%,j% ! für Pixelkoordinaten
LOCAL z_re_h ! für Iteration
LOCAL z_re_m,z_im_m
v_re_schritt=wk/w% ! Schrittweite horizontal
v_im_schritt=-hk/h% ! Schrittweite vertikal
v_im=yk ! Startwert vertikal/oben
FOR j%=y% TO y%+h%
v_re=xk ! Startwert horizontal/links
FOR i%=x% TO x%+w%
z_re_m=a ! Iteration Mandelbrot
z_im_m=b ! z-Werte konstant
zaehler%=0
WHILE zaehler%<max_iter% AND z_re_m*z_re_m+z_im_m*z_im_m<4
z_re_h=z_re_m
z_re_m=z_re_m*z_re_m-z_im_m*z_im_m+v_re
z_im_m=2*z_re_h*z_im_m+v_im
INC zaehler%
WEND
' Die folgende Farbbestimmung könnte man auch
' in einer Zeile zusammenfassen, aber das würde
' geringfügig komplizierter.
IF zaehler%>=max_iter%
COLOR 1
ELSE
COLOR -((zaehler%<=max_iter% DIV 2) AND (zaehler% MOD 2=1) AND ((i%+j%) MOD 2=1))
ENDIF
' Ohne Grauabstufung:
COLOR -(zaehler%>=max_iter%)
' Für Farbe (Bsp.: 8 Farben) :
' If Zaehler%>=Max_iter%
' Color=0
' Else
' Color (Zaehler% Mod 7)+1
' Endif
PLOT i%,j% ! Ausgabe
ADD v_re,v_re_schritt
NEXT i%
ADD v_im,v_im_schritt
NEXT j%
RETURN
' Ende
Listing 5: Der komplette Fractal-Generator
'
' (c) MAXON Computer 1989
'
' Fractal: Pixelausgabe
PROCEDURE plot_pixel(xp%,yp%,it%)
' Konvergenzgebiet (schwarz/weiß):
' If It%>=Max_iter%
' Plot Xp%,Yp%
' Endif
' Konvergenzgebiet (schwarz/grau/weiß):
IF it%>=max_iter%
PLOT xp%,yp%
ELSE
IF (it%<=max_iter% DIV 2) AND (it% MOD 2=1) AND ((xp%+yp%) MOD 2=1)
PLOT xp%,yp%
ENDIF
ENDIF
RETURN
Listing 4: Pixelausgabe