Da wir uns dem Ende dieser Serie nähern, wird es Zeit, sich mit den neueren Methoden der KI und damit auch den Grundlagen menschlicher Intelligenz zu beschäftigen. Denn wie jeder weiß, ist das menschliche Gehirn jedem Computer auf der Welt überlegen, wenn es um sensorische Fähigkeiten und die Fähigkeit zur Abstraktion und Assoziation geht. In diesem Teil möchte ich Sie deshalb mit dem elementaren Aufbau des Gehirns vertraut machen. Und natürlich soll ein Programm die praktische Nutzanwendung (oder einen allerersten Versuch dazu) demonstrieren.
Das Neuron: Das Gatter des biologischen Computers
Basis jeglicher nervlicher Aktivität im menschlichen Körper ist eine spezialisierte Form von Körperzellen, dem Neuron. Abb. 1 zeigt eine schematische Darstellung eines Neurons. Die eigentliche Zelle enthält eine Vielzahl dünner, verästelter Ausläufer, die sogenannten Dendriten. Diese stellen den Kontakt zu benachbarten Neuronen her. Auffällig ist der lange Fortsatz der Zelle, das sogenannte Axon. Dieses bis zu einem Meter lange Axon leitet einen Impuls der Neuronenzelle an die Dendriten benachbarter Neuronen weiter. Uber dieses lange Axon (auch unter dem Begriff Nervenfaser bekannt), erfolgt beispielsweise die Mitteilung an das Schmerzzentrum im Gehirn. Uns interessiert hier natürlich weniger die Nervenleitung, als die Wirkung eine? neuralen Netzes, eines Ganglions. Wer sich näher für die Funktionsweise eines Neurons interessiert, findet in [1] und [2] leicht verständliche Darstellungen.
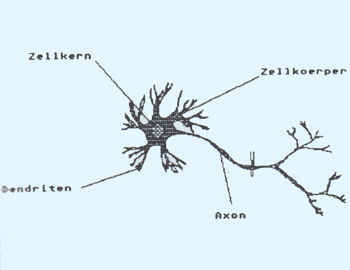 Abb. 1: Schematische Darstellung eines Neurons
Abb. 1: Schematische Darstellung eines Neurons
Diese Neuronen bilden Netzwerke Normalerweise herrscht an der Zellmembran ein Potential von -70mV. D. h., das Innere der Zelle ist negativ geladen gegenüber dem äußeren Teil der Membran. Dies rührt daher, daß in der Membran befindliche Proteine Na+-Ionen aus der Zelle herauspumpen. An den Enden der Dendriten befinden sich Kanäle, die in der Regel geschlossen sind, unter Umständen aber geöffnet werden können und durch die Na +-Ionen im geöffneten Zustand nahezu mühelos in die Zelle gelangen können. Dann steigt das Potential im Innern der Zelle wieder an. Überschreitet das Potential einen bestimmten Grenzwert (ca. +20mV), dann bricht ein Chaos aus! Das Neuron pumpt Na+-Ionen in das Axon, so daß sich über die Membran des Axons eine Depolarisierung ausbreitet. Das Neuron feuert einen Impuls ab. Der zeitliche Verlauf dieses Aktionspotentials ist in Abb. 2 dargestellt. Kurz nach dem Feuern des Neurons braucht es eine Ruhephase, in der kein weiterer Impuls abgefeuert werden kann (absolute Ruhephase).
Daran schließt sich eine relative Ruhephase an, in der eine Anregung manchmal zum Abfeuern führt, manchmal aber auch nicht (relative Ruhephase). Erst danach hat sich das Neuron erholt und reagiert wie gewohnt. Am Ende des Axons befindet sich wieder ein Dendrit eines Neurons, das wiederum angeregt wird. Manchmal gelangen Substanzen durch die Kanäle der Synapsen (Stelle an der Axon des anregenden Neurons und Dendrit des angeregten Neurons Zusammentreffen), die das Potential im Innern der Zelle noch negativer werden lassen. In diesem Fall wirkt das Neuron beim Feuern nicht anregend (excitatorisch), sondern verhindernd (inhibitorisch). Weiterhin ist interessant, wo das Neuron angeregt wird.
Je näher der Dendrit am Axon sitzt, desto stärker wirkt sich das Einströmen von K+-Ionen auf das Axon aus, d. h. das Neuron erfährt einen stärkeren Potentialanstieg. Außerdem können sich benachbarte Neuronen bei Anregung gegenseitig verstärken, da im gleichen Raumgebiet eine lokale Erhöhung der Na+-Konzentration erfolgt. In Wirklichkeit laufen diese Vorgänge natürlich sehr komplex ab. Erstens hat ein Neuron hunderte von Dendriten, zweitens kann sich ein Neuron auch selbst erregen (über einen Ausläufer des Axons an einen eigenen Dendriten). Um aber einen Einblick in den Mechanismus eines Ganglions zu bekommen, habe ich das Programm GANGLION in die PD gegeben. Es ist in C geschrieben (Megamax) und simuliert ein Ganglion, bestehend aus 8 peripheren Neuronen und einem Zentralneuron. Beim Starten des Programms werden die Neuronen per Zufallsgenerator auf Excitatorisch oder Inhibitorisch eingestellt. Abb. 3 zeigt das Bild nach dem Einschalten. Die Wirkung eines Neurons kann mit Hilfe des Menüpunktes ’Wir-kung’ der Menüleiste geändert werden. Man klickt den Menüpunkt an und anschließend das Neuron, dessen Wirkung geändert werden soll. Ansonsten klickt man das Neuron an, das gezündet werden soll. Hat das Neuron gezündet, erkennt man das einerseits daran, daß der Inhalt invertiert wird, andererseits steigt das Potential im Innern des Neurons. Wird ein ’excitatives Neuron’ dicht am Axon gezündet, wird das Neurons sofort feuern. Ist die Wirkung des Neurons ’inhibitorisch’, fällt das Potential unter -70mV und verhindert damit ein Zünden bei der nächsten ’excitatorischen’ Anregung. Das gezündete Neuron bleibt für die Dauer der absoluten Erholungsphase invertiert dargestellt. Der Leser möge mit dem Programm spielen und die Zusammenhänge, die (unendlich komplexe) Grundlage unseres Denkens darstellen und auf sich wirken lassen.
 Abb. 2: Der zeitliche Verlauf eines Aktionspotentials
Abb. 2: Der zeitliche Verlauf eines Aktionspotentials
Die Matrix: Das biologische Speichermedium mit mathematischen Hintergrund
Nachdem sie nun gesehen haben, wie ein Netzwerk von Neuronen zusammenwirkt, bleibt die Frage, wie dieser physiologische Aufbau zum Denken, d. h. zum Lernen und Speichern von Informationen benutzt werden kann. Fassen wir das Ergebnis des vorigen Abschnitts nochmals in Abb. 4 zusammen. Die Synapsen an den Dendriten eines Neurons erhalten Signale von dem Axon eines verbundenen Neurons. Im Innern der Zelle werden die Signale der Neuronen addiert. Das Neuron feuert, wenn ein Schwellwert überschritten wird. Die miteinander verbundenen Neuronen bilden ein Netzwerk, wie es in sehr einfacher Form Abb. 5 zeigt.
Gestrichelt sind dort die inhibitorisch wirkenden Verbindungen eingezeichnet und solide die exhibitorisch wirkenden Verbindungen. Wie man sieht, läßt sich das gleiche Netzwerk in graphischer und in Matrizenform darstellen. In der Letzteren wird eine exhibi-torische Verbindung als +1 an der entsprechenden Stelle eingetragen, eine inhibitorische Verbindung als -1 und keine Verbindung als 0. Mit Hilfe solch einer Matrix ließe sich das Verhalten eines einfachen Neuronenkomplexes bereits simulieren. Aber wo steckt die Information?
Digitale Mustererkennung
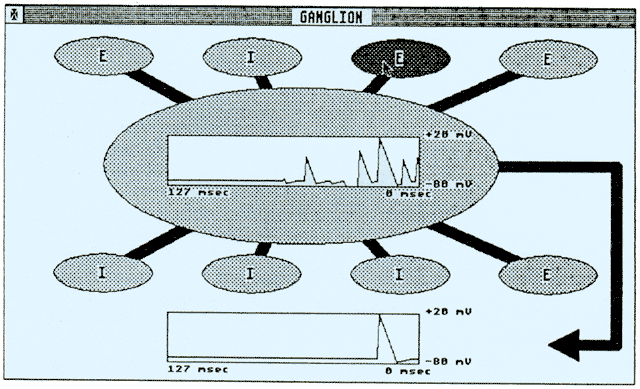 Abb. 4
Abb. 4
Besonders anschaulich ist der Prozeß des Lernens und Erinnerns von Informationen am Beispiel der Mustererkennung. Bekanntlich erhalten wir unser Sehvermögen durch eine Vielzahl von Sehnerven, die in der Netzhaut ausliegen und durch Licht angeregt werden. In unserem einfachen Neuronenmodell entspricht das einer rechteckigen Anordnung von Neuronen.
In Abb. 6 sind neun Neuronen gezeigt, die ein Bild des Buchstabens I erhalten. Für eine brauchbare Mustererkennung sind mehr als nur 9 Neuronen erforderlich, aber es wird auch so schon kompliziert genug. Die Information ob ein Neuron belichtet wird oder nicht, ist in dem Zustandsvektor V gespeichert. Eine 1 bedeutet, daß ein Teil des Buchstabens über dem Neuron liegt. Eine 0 bedeutet kein Signal für das Neuron. Wenn nun ein Bildwechsel erfolgt, soll sich das Gedächtnis wieder erinnern, wenn erneut ein I als Eingangssignal vorliegt, d. h. der Zustandsvektor identisch ist.
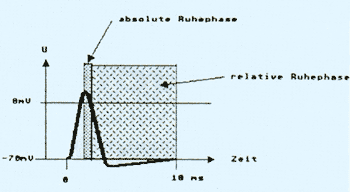 Abb. 3: Potentialverlauf nach dem Einschalten
Abb. 3: Potentialverlauf nach dem Einschalten
Wie wir aus dem oberen Abschnitt noch wissen, ist ein Neuron auf Grund seiner Dendriten und axonalen Verzweigungen in der Lage, mit jedem anderen Neuron eine Verbindung herzustellen. Die Information, wie eine Verbindung wirkt, stellen wir wieder als 1 (excitatorisch) oder -1 (inhibitorisch) dar. Und wie die Wirkung sein soll, bestimmen wir aus dem Zustandsvektor in der Lernphase. Es gibt verschiedene Lernregeln, nach denen der Wert der Lemmatrix berechnet werden kann. Wir verwenden in dem Programm NEURAL.PAS (Listing 1) ausschließlich die Hopfieldschen Lernregel. Wer sich stärker für dieses Thema interessiert und einen einführenden Ubersichtsartikel über Wissensspeicherung in neuralen Netzen sucht, sei an [3] und [4] verwiesen.
Nach der Hopfieldschen Lernregel berechnet sich die Zustandsmatrix aus deren vorliegendem Wert und dem Zustandsvektor:
Gl.1
Wij = Wij + (2*Vi-1)*(2*Vj-1)
Mit anderen Worten sagt Gl.1: der neue Wert der Matrix in der Spalte i und der Zeile j ist gleich dem alten Wert zuzüglich +1 oder —1. Und zwar wird 1 addiert, wenn die i-te Stelle und die j-te Stelle des Zustandsvektors V entweder beide 0 oder beide 1 sind. Haben beide Stellen des Zustandsvektors verschiedene Werte, so wird 1 subtrahiert. Damit ist klar, daß die Matrixelemente dort betragsmäßig erhöht werden, wo oft dasselbe Muster erscheint. Das Muster prägt sich der Matrix langsam ein, der Lernprozeß hat begonnen.
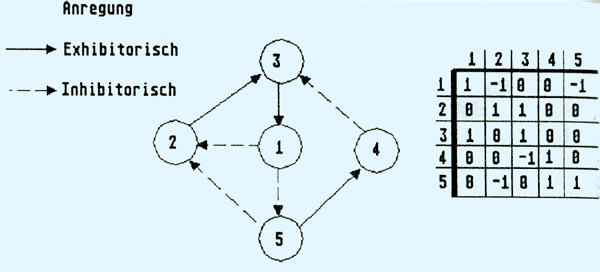 Abb. 5
Abb. 5
Erinnerung an Gelerntes
Nachdem der Matrixspeicher genügend Gelegenheit zum Lernen hatte, überlegen wir uns nun, wie man seine Erinnerung wecken kann. Dazu müssen wir den momentan vorliegenden Zustandsvektor mit der Lernmatrix verknüpfen:
Gl.2 V’ = V * W
In dieser einfachen Form ist auf die Berücksichtigung eines konstanten Eingangssignals und des Schwellwertes der Einfachheit halber verzichtet worden. Hierin bedeutet V’ den Ausgangszustandsvektor, V den Eingangszustandsvektor und W die Lernmatrix. Nach den Regeln der Multiplikation einer Matrix mit einem Vektor errechnet sich somit die i-te Komponente des Ausgangszustandsvektors V’ zu:
Gl.3
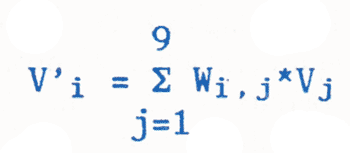
In Abb. 6 ist die Lernmatrix W nach einmaligem Lernvorgang für 9 Neuronen, sowie der sich daraus ergebene Zustandsvektor und das entsprechende Muster dargestellt.
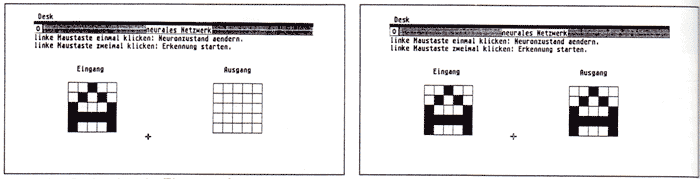
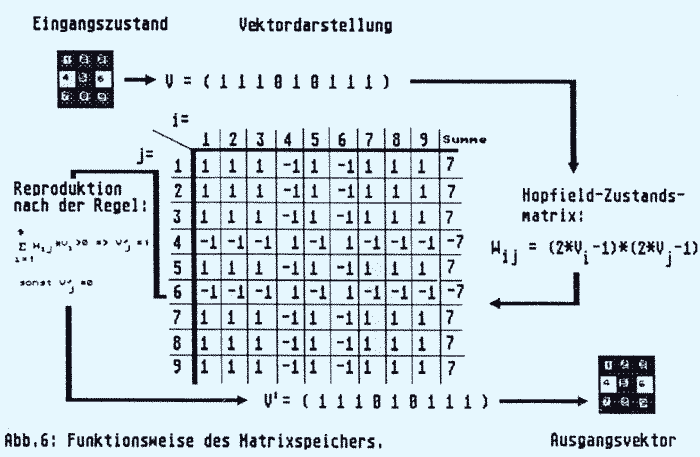 Abb. 7: Der Buchstabe A im Eingangsvektor. / Abb. 8: Der Eingangszustand wurde gelernt.
Abb. 7: Der Buchstabe A im Eingangsvektor. / Abb. 8: Der Eingangszustand wurde gelernt.
Lohnt sich der Aufwand?
Um selbst Erfahrung mit dem Matrixgedächtnis sammeln zu können, habe ich das Programm NEURAL.PAS geschrieben (Listing 1). Es ist mit ALICE Pascal entwickelt, da es so schneller läuft. Für Benutzer anderer Pascal Versionen sollte die Umsetzung keine Schwierigkeiten bereiten. Interessierte ohne Pascal Interpreter oder Compiler finden auf der Programmdiskette dieses Heftes den Run-Only-Interpreter APRUN, mit dessen Hilfe das Programm gestartet werden kann.
Abb. 7 zeigt den Bildschirm nach dem Start des Programms und einer kleinen Copyright Nachricht. Der Fadenkreuzcursor kann jetzt in das Eingabefeld bewegt werden. Durch Anklicken eines Feldes wird das Feld (entspricht einem Neuronenmodell) schwarz dargestellt (Neuron aktiv). Abb. 8 zeigt den Bildschirm nach der Eingabe des Buchstabens A. Natürlich erscheint nun auch das gleiche Muster in der Ausgabe. Wir lassen mit Hilfe mehrerer Doppelklicks die Matrix den Buchstaben lernen. Anschließend geben wir ein verrauschtes Exemplar desselben Buchstabens ein und lassen die Ausgabe berechnen.. Wie Abb. 9 eindeutig zeigt, erhält man ein fehlerfreies Ergebnis.
Heureka. Ist es nicht gerade diese Eigenschaft, die menschliches Erkennen auszeichnet? Das Erkennen von undeutlichen oder mehrdeutigen Signalen? Es scheint, als wäre man mit dem Matrixgedächtnis dem Geheimnis natürlicher Intelligenz ein ganz klein wenig näher gekommen. Noch etwas ist phantastisch an diesem primitiven Matrixspeicher. Als nächstes geben wir (ohne das Programm zwischendurch gestoppt zu haben) den Buchstaben X ein. Abb. 10 zeigt, daß die Matrix den Buchstaben X zusätzlich gelernt hat. Überprüfen Sie das gerne, indem Sie nacheinander X, A, X etc. eingeben. Immer erhalten Sie die richtige Antwort. Wenn nicht, haben Sie einfach nicht lange genug gelernt (wie menschlich!!). Aber Halt! Nicht gleich übermütig werden! Falls Sie versucht haben sollten, mehr als zwei Buchstaben zu lernen, wird die kleine Matrix Sie leider mit einem wirren Muster enttäuschen müssen (oder nennt man das vielleicht Kreativität?).
Weiterführende Anwendungen
Natürlich läßt sich das Verfahren noch erheblich verbessern. So fehlt beispielsweise ein Eichfaktor, der mit dem Eingangssignal des Neurons multipliziert, die Position der Synapse berücksichtigt. Und auch die Schwellwertfunktion wurde vernachlässigt. Und selbstverständlich ist es nicht der Sinn der Matrixspeicherung, das Bild des Eingangsvektors zu reproduzieren. Vielmehr soll mit dem Vektor anschließend etwas gemacht werden. Beispielsweise die Zuordnung des ASCI Zeichens an das gelesene Muster. Oder im Bereich der Spracherkennung denke man sich das Sprachsignal einer Fourieranalyse unterzogen, und die daraus resultierende Frequenz-Zeit-Matrix wird in einem Matrixspeicher gespeichert und der gesprochene Satz niedergeschrieben. Vielleicht ist dir der Weg zur vollautomatischen Schreibmaschine? Wer sich näher für das assoziative Gedächtnis interessiert, sollte bei [5] nachlesen.
Dr. Sarnow
 Abb. 9: Erkennung einer unvollständigen Eingabe. / Abb. 10: Die gleiche Matrix kann noch einen weiteren Eingangszustand lernen.
Abb. 9: Erkennung einer unvollständigen Eingabe. / Abb. 10: Die gleiche Matrix kann noch einen weiteren Eingangszustand lernen.
Literatur
[1] B. Douglass, 80 Microcomputing April 1982, Copernicae Mathema-ticae, p. 382.
[2] Spektrum der Wissenschaft, Sonderband Gehirn und Nervensystem Heidelberg 1987.
[3] C. Jorgensen, C. Matheus: Catching Knowledge in Neural Nets. AI Expert, December 1986, p. 30 ff
[4] S. B. Schreiber, Großer Auftritt für eine kleine Matrix, c’t, Jul: 1987, p. 106 ff.
[5] T. Kohonen: Self-organisation and associative memory. Springer Verlag, Berlin, 1984.
program netzwerk(input, output);
{Simulation eines neuralen Netzwerkes}
{ ALICE Benutzer MERGEen hier die Bibliothek GRAPHLIB.AP }
{ Benutzer anderer PASCAL Versionen Includen hier die GEMLIB }
const
anzahl = 25; {Anzahl Neuronen im Netzwerk}
zeile = 5; {Anzahl Neuronen pro Zeile}
py = 100; {y-koordinate der Rechteckfelder}
pxe = 70; {x-koordinate des Eingangsfeldes}
pxa = 350; {x-Koordinate des Ausgangsfeldes}
breite = 20; {Breite eines Feldes}
type
zustand = array [1..anzahl] of integer; {Zustaende der einzel nen Neuronen}
matrix = array [1..anzahl] of array [1..anzahl] of integer; { Relationsmatrix}
var
eingang, ausgang : zustand; {
EingangsSignal des neuralen Netzwerkes und Ausgang auf Grund d es neuralen Lemvorganges}
w : matrix; {Die Relationsmatrix der neuralen Zustaende}
i, j, ereignis, mx, my, neuron_nr : integer;
fenster : text;
menueleiste : Pointer;
procedure hopfield(eingang: zustand; var w: matrix);
{Hopfield’sehe Lemregel}
var
i, j : integer;
begin
for i := 1 to anzahl - 1 do begin
for j := i + 1 to anzahl do begin
w[i][j] := w[i][j] + (2*eingang[i] - 1)*(2*eingang[j] -1 );
w[j][i] := w[i][j];
end;
end;
end;
procedure zeige_neuron(n: integer);
{Zeigt den Zustand des n-ten Neurons}
var
i, j, k : integer;
punkte : array [1..4] of record
x, y : integer;
end;
begin
i := (n - 1) mod 5;
j := (n - 1) div 5;
if eingang[n] > 0 then begin
FillPattern(1);
end
else begin
FillPattern(O);
end;
for k := 1 to 4 do begin
with punkte[k] do begin
x := pxe + i*breite + ((k - 1) mod 2)*breite;
y := py + j*breite + (k mod 2)*breite;
end;
end;
w_bar(punkte);
end;
procedure zeig_zustand ;
{Zeigt den Zustand des Eingangs- und Ausgangsfeldes an}
var
i, j, k : integer;
punkte : array [1..4] of record
x, y : integer;
end;
begin
for i := 1 to zeile do begin
for j := 1 to zeile do begin
zeige_neuron(i + (j - 1)*5);
if ausgang[i + (j - 1)*5] > 0 then begin
FillPattern(1);
end
else begin
FillPattern(0);
end;
for k := 1 to 4 do begin
with punkte[k] do begin
x := pxa + i*breite + ((k - 1) mod 2)*breite;
y := py + (j - 1)*breite + (k mod 2)*breite;
end;
end;
w_bar(punkte);
end;
end;
end;
procedure neuer_ausgang(var ausgang: zustand; w: matrix);
{
Berechnet den neuen Ausgangszustand aus der gelernten Matrix
und den Eingangszustand}
var
zwischen : zustand;
i, j, summe : integer;
begin
for i := 1 to anzahl do begin
summe := 0;
for j := 1 to anzahl do begin
summe := summe + w[i][j]*eingang[j];
end;
if sumne > 0 then begin
ausgang[i] := 1;
end
else begin
ausgang[i] := 0;
end;
end;
end;
function finde_neuron(mx, my: integer) : integer;
{
Diese Funktion gibt die Nummer des Neurons (1..25) zurueck, welches von der Maus angeklickt wurde}
var
i, j : integer;
begin
if ((mx < pxe + 5*breite) and (mx > pxe) and (my > py) and (my < py + 5*breite)) then begin
i := (mx - pxe) div breite;
j := (my - py) div breite;
finde_neuron := j*zeile + i + 1;
end
else begin
finde_neuron := 0;
end;
end;
{Hauptprogramm}
begin
RemoveEditWindows;
Close(output);
GemStart ;
menueleiste := NewMenuBar ;
DisplayMenuBar(menueleiste);
Assign(fenster, 'neurales Netzwerk');
QuickWindow(fenster, WOtitle or WOclose or WOclicks, 0);
GraphicsWindow(fenster);
writeln(fenster, 'linke Maustaste einmal klicken: Neuronzustacd aendern.');
writeln(fenster, 'linke Maustaste zweimal klicken: Erkennung starten.');
writeln(fenster);
writeln(fenster);
writeln(fenster, ' Eingang Ausgang');
for i := 1 to anzahl do begin
eingang[i] := 0;
ausgang[i] := 0;
for j := i to anzahl do begin
w[i][j] := 0;
w[j][i] := 0;
end;
end;
i := Alert(1, '[1][<c> Dr. Samow|geschrieben in|ALICE-Pascal][Alles klar?]’);
zeig_zustand ;
MouseType(7);
repeat
ereignis := GetEvent(true);
if ereignis = Eclick then begin
if EventParameter(0) = 1 then begin
mx := EventParameter(1);
my := EventParameter(2);
neuron_nr := finde_neuron(mx, my);
if neuron_nr > 0 then begin
if eingang[neuronnr] = 0 then begin
eingang[neuron_nr] := 1;
end
else begin
eingang[neuron_nr] := 0;
end;
zeige_neuron(neuron_nr);
end;
end;
if EventParameter(0) = 2 then begin
MouseType(2);
hopfield(eingang, w);
neuer_ausgang(ausgang, w);
zeig_zustand ;
MouseType(7);
end;
end;
until ereignis = Eclose;
MouseType(0);
GemFinish ;
end.
Listing 1: Simulation eines neuralen Netzwerks