Bilderspiele: Faszination Computergrafik (2)

Der zweite Teil unserer Grafikserie hat sich wegen einer ausgedehnten Urlaubsreise des Autors leider etwas verzögert. Nachdem jetzt aber die gesamte Urlaubsfaulheit abgeschüttelt wurde, geht es weiter (und richtig los).
In der letzten Folge hatten wir uns mit dem Unterschied zwischen raster- und objektorientierten Grafiksystemen beschäftigt. Um diese Unterschiede noch einmal kurz zusammenzufassen: Ein rasterorientiertes System weiß nicht was es tut, es dient lediglich dazu, Werkzeuge, die direkt ein Raster, wie zum Beispiel den Bildschirm, mit Werten füllen, zur Verfügung zu stellen. Diese Methode hat den Nachteil, daß sie Informationen über die Beschaffenheit des Rasters voraussetzt und außerdem nicht ohne weiteres Änderungen an Einzelteilen der Darstellung erlaubt, da es ja nicht weiß, was überhaupt dargestellt ist.
Im Gegensatz dazu basiert ein objektorientiertes System darauf, daß vom Anwender die Objekte, die dargestellt werden sollen, beschrieben werden. Die Darstellung des Objektes, das heißt, die Umsetzung in das für das jeweilige Ausgabegerät geeignete Rasteroder Vektorformat übernimmt dann das System. Um ein einzelnes Objekt der Zeichnung zu verändern, genügt es, seine Beschreibung zu editieren, das System kann dann eine neue Zeichnung anfertigen.
Daraus folgt, daß auch für ein objektorientiertes System Zeichenroutinen erforderlich sind, die ein Objekt auf dem Bildschirm darstellen. Um diesen Kern herum müssen aber Routinen liegen, die 1. die Objekte verwalten, 2. die Transformierung in ein für die Malroutinen geeignetes Format erledigen.
Im Betriebssystem des ST sind eine ganze Reihe von Zeichenroutinen bereits vorhanden, mit deren Hilfe es eigentlich nicht sehr schwierig ist, ein rasterorientiertes Grafikprogramm zu schreiben. Das beweist auch die Flut von Malprogrammen für den ST.

Wie sehen aber nun grafische Objekte aus, wie kann man sie darstellen und manipulieren?
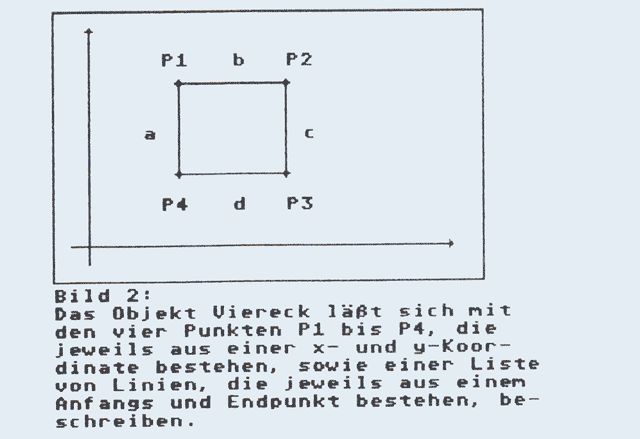
Das einfachste aller Objekte ist mit Sicherheit der Punkt. Um einen Punkt zu beschreiben, verwendet man ein Koordinatensystem (Bild 1). Die Koordinaten eines Punktes beschreiben seine Lage in bezug auf einen Ausgangspunkt, den Koordinatenursprung. Kompliziertere Objekte beschreibt man im einfachsten Fall als eine Menge von miteinander durch Linien verbundenen Punkten (Bild 2).
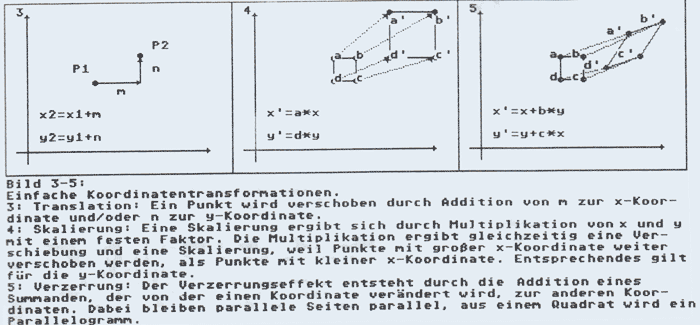
In den Bildern 3-6 sehen Sie einige Möglichkeiten, mit denen man Punkte oder Objekte aus Punkten und Linien im Koordinatensystem manipulieren kann. Es läßt sich leicht nachweisen, daß es völlig genügt, die Endpunkte einer Linie zu manipulieren, um damit die ganze Linie analog mitzuverändern. Es ist also nicht nötig, alle Punkte einer Linie zu bearbeiten. In einer realen Welt wäre es auch unmöglich, besteht doch eine Linie aus unendlich vielen Punkten.
Wie man in den Bildern sieht, gibt es eine ganze Menge von Möglichkeiten, einen Punkt zu manipulieren. Es wäre natürlich schön, wenn es für alle diese Möglichkeiten eine geeignete mathematische Methode gäbe, die es erlaubte, alle Operationen 1. einheitlich und 2. auf einmal zu erledigen. Glücklicherweise gibt es tatsächlich eine solche Möglichkeit. Bitte haben Sie Verständnis dafür, daß die folgenden Erklärungen aus Platzmangel nicht dafür gedacht sind, das Rechnen mit Vektoren und Matrizen lückenlos zu erklären. Es gibt eine Menge Mathebücher, die sozusagen sehnsüchtig auf diese Gelegenheit gewartet haben. Im folgenden soll nur kurz die Praxis erläutert werden.
Fassen wir doch einmal die Gleichungen aus den obigen Bildern zusammen. Für die Bilder 3-5 ergibt sich:
(1) xneu = ax + by + m und
(2) yneu = cx + dy + n
Dabei sind die Variablen a und d für eine Skalierung, b und c für eine Verzerrung und m und n für eine Verschiebung verantwortlich. Es ist leicht ersichtlich, daß eine Rotation dann entsteht, wenn in der ersten Gleichung
a = cos(phi) und b = -sin(phi) ist und in der Zweiten c= sin(phi) und d = -cos(phi).
Offensichtlich ist also eine Rotation um den Ursprung bereits eine kombinierte Operation, die aus einer Skalierung und einer Verzerrung besteht.
Die beiden Gleichungen (1) und (2) bilden zusammen eine Einheit, die man ein lineares Gleichungssystem nennt. Ein lineares Gleichungssystem kann man aber auch anders formulieren:
(3) P2 = T*P1 mit P1=(x,y),P2 = (xneu,yneu), T = a b / c d
In dieser Schreibweise sind P2 und P1 Vektoren und T eine Matrix, die die nötigen Parameter enthält. Eigentlich ist dies nichts weiter als eine Kompaktschreibweise für ein lineares Gleichungssystem. Ihnen wird sicherlich auffallen, daß die Parameter für die Translation in der Matrix T fehlen. In einer Matrix aus 2 * 2 Elementen gibt es leider keine Möglichkeit, Translationen einzubauen. Dieses Problem ist aber leicht lösbar, doch dazu später mehr.
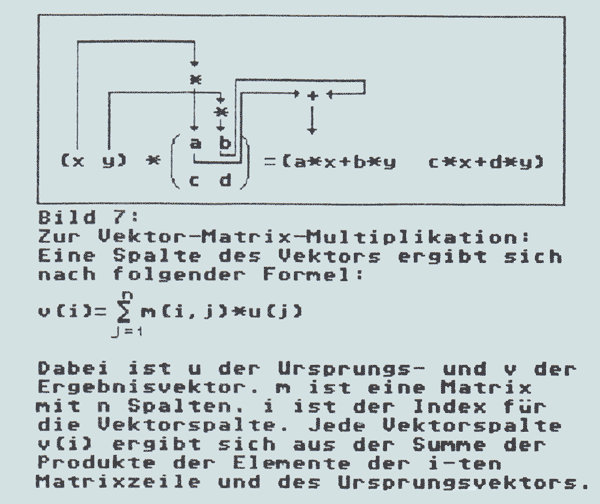
Zur Erklärung der Multiplikation einer Matrix mit einem Vektor betrachten Sie bitte Bild 7. Das wirklich praktische an einer Matrix ist aber, daß man sie nicht nur mit Vektoren, sondern auch mit anderen Matrizen multiplizieren kann (Bild 8). Wollen Sie also verschiedene Transformationen kombinieren, brauchen Sie nur die entsprechenden. Matrizen zu basteln (indem Sie für eine Skalierung z. B. die entsprechenden Werte für a und d ein-setzen). Für eine einfache Transformation ist das ganz einfach. Um jetzt alle gewünschten Transformationen auf einmal durchzuführen, brauchen Sie nur die Matrizen zu multiplizieren und dann ihre Punkte der Reihe nach mit dem Ergebnis zu multiplizieren. Einfach, nicht?
Nun aber zurück zur Translation. Um eine Verschiebung zu ermöglichen, fügen wir dem Punktvektor P einfach eine dritte Komponente, die den Wert h haben soll, und der Matrix T eine dritte Reihe und Spalte von Parametern zu:
Ausmultipliziert ergibt das:
xneu = ax + by + m
yneu = cx + dy + n
h =0 + 0 + 1
Da die dritte Zeile sich nicht verändert hat, können wir sie ignorieren. Diese Art der Darstellung von zweidimensionalen Koordinaten mit einer dritten Hilfskoordinaten nennt man homogene Koordinaten. Wenn der Wert s in Gleichung 4 einen anderen Wert annimmt, ergibt sich eine globale Skalierung: Die tatsächlichen Werte für xneu und yneu erhält man erst nach Division durch s.
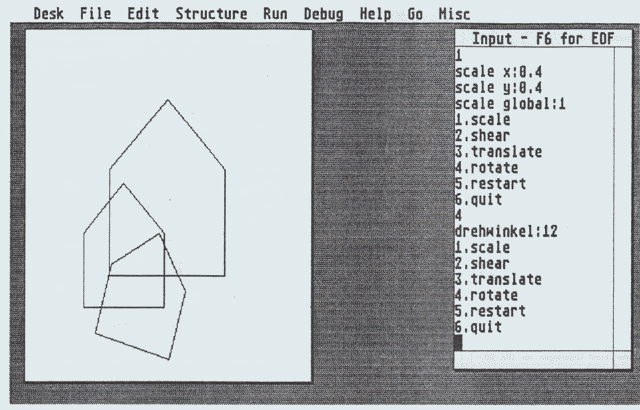
Diese Folge der Grafikserie möchte ich mit einem Programm abschließen, daß zum Ausprobieren der Transformationsmatrix dient. Es ist in Pascal geschrieben, verwendet aber keine Funktionen, die man nicht in GfA-oder Omikron-Basic simulieren könnte. Auch die Übersetzung nach C dürfte kein Problem sein.
Das Programm benutzt eine Technik, die in großen Grafiksystemen üblich ist, weil die Ausgabe der Grafiken auf verschiedenen Geräten möglich sein muß: Die Speicherung und Transformierung des Beispielobjektes erfolgt in einem sogenannten normalisierten Koordinatensystem, das so auf dem Bildschirm nicht darstellbar ist. Erst zum Zeitpunkt der Ausgabe werden die Bildpunkte in das Bildschirmkoordinatensystem übersetzt. Damit ist das Programm extrem leicht an verschiedene Ausgabegeräte und -auflösungen anpaßbar. Das verwendete System reicht auf beiden Koordinatenachsen von 0 bis 1. Einzelne Punktkoordinaten müssen also dazwischen liegen.
Das Programm enthält einige allgemeine Routinen zur Bearbeitung von Matrizen:
Die Prozedur null_mat2dh füllt eine aus 3-*3 Elementen (Die Abkürzung 2dh am Ende ihres Namens bedeutet ’2-Dimensional, homogen’ - das wird sich noch ändern, wenn der Raum dazukommt!) bestehende Matrix mit Nullen. Eine Nullmatrix verhält sich wie eine Null beim normalen Rechnen: Alles was damit multipliziert wird, ergibt Null.
ident_mat2dh macht aus einer Matrix eine Einheitsmatrix. Das ist eine Matrix, die sich wie die 1 bei der normalen Multiplikation verhält. Frage: Wie muß eine solche Matrix aussehen? (Folgen Sie den Rechenregeln!)
null_vec2dh - das gleiche für einen Vektor, was null_mat2dh für eine Matrix ist.
matmul2dh: Multipliziert zwei Matrizen.
vecmat2dh: Multipliziert einen Vektor mit einer Matrix.
Wie funktioniert dieses primitive Grafiksystem? Zuerst einmal wird, wie immer, alles initialisiert. Dabei wird die Transformationsmatrix t mit den Werten der Einheitsmatrix aufgefüllt.
Dann wird das Originalbild gezeichnet. In einer Schleife kann jetzt die Matrix t mit den wildesten Transformationen gefüllt und das Ergebnis angezeigt werden. Dabei wird immer wieder das Original transformiert, nicht eine Transformation nach der anderen mit dem bereits transformierten Bild ausgeführt. Mit der ’restart’-Option kann die Matrix t wieder initialisiert werden.
Der Ablauf der Transformationen ist der folgende: Zuerst füllt jede der Routinen set_scale, set_trans, set_rot und set_shear eine eigene Matrix mit den eingegebenen Werten. Diese Matrix wird dann mit t multipliziert und das Ergebnis in t zurückgeschrieben. Damit enthält t nach dem Aufruf einer der set_Prozeduren eine neue Kombination von Transformationen.
Dann wird die Prozedur do_transform aufgerufen. Sie multipliziert jeden der Punkte des Objektes mit t. Danach wird noch die Korrektur für den globalen Scaling-Faktor s durchgeführt. Das Ergebnis ist das manipulierte Objekt, das sich allerdings immer noch im normalisierten Koordinatensystem befindet.

Deshalb wird die Prozedur do_view aufgerufen. Von hier aus wird die view_trans-Funktion aufgerufen, die die normalisierten Koordinaten in Bildschirmkoordinaten übersetzt. Am Anfang des Programmes befinden sich die Konstanten, die die dafür notwendigen Werte des Bildschirmkoordinatensystems enthalten. Danach wird das Objekt gezeichnet.
Dieses Verfahren der aufeinanderfolgenden Transformationen ist wichtig. Um das Programm an 3D-Transformationen anzupassen, muß nur eine Transformation eingefügt werden, die die dreidimensionalen Koordinaten auf eine Fläche projeziert. Natürlich müssen auch die Datentypen geändert werden. Aber der prinzipielle Aufbau bleibt gleich. Hier sieht man auch den großen Vorteil von Matrizen-Mathematik noch einmal sehr deutlich: Für die Anpassung an drei Dimensionen muß ich nur die Größe der Matrizen und der Vektoren ändern. Die Routinen sehen ansonsten völlig gleich aus.
Für eine Anpassung an andere Auflösungen müssen also nur die Parameter für eine Prozedur geändert werden. Eventuell muß auch die Formel in dieser Prozedur geändert werden, aber nur dann, wenn sich das Koordinatensystem des Ausgabegerätes erheblich von dem des Bildschirmes unterscheidet.
Drei weitere Prozeduren sind systemabhängig: Im Hauptteil des Programmes wird eine Routine zum Löschen des Bildschirms aufgerufen. Die do_view-Routine zeichnet Linien mit Hilfe einer Funktion draw. Schließlich wird in der Prozedur init die Grafikausgabe des verwendeten Pascal-Systems initialisiert. Dabei handelt es sich um Alice, einen Pascal-Interpreter, den ich zum Testen von Algorithmen nur empfehlen kann.
Im folgenden die Änderungen für CCD-Pascal, die ich aus Zeitmangel allerdings nicht mehr testen konnte (Weitere Hinweise in den Kommentaren im Programm):
- Koordinaten-Konstanten: xmax:639; ymax:399; xstart:0; ystart:399
- ClrScr(Fenster) ersetzen durch Clear_Screen
- Draw(x1,y1,x2,y2) ersetzen durch line(x1,y1,x2,y2,1,0,0,0,lmode,0).
’lmode’ muß vorher als $FFFF definiert werden.
Das Programm als ’TOS’ compilieren. Das war’s.
Zum allerletzten Schluß noch ein paar Aufgaben:
- Wie sieht die Matrix für eine Spiegelung eines Punktes an der x- oder y-Achse des Koordinatensystems aus?
- Welchen geometrischen Sinn könnten die Parameter der Matrix aus Gleichung 4 haben, die dort den Wert 0 besitzen?
- Schreiben Sie eine Routine, die ein Objekt um seinen Mittelpunkt und nicht um den Nullpunkt rotieren läßt. Lösen Sie das Problem allgemein, also: Wie kann man ein Objekt um einen beliebigen Punkt rotieren lassen?
- Ändern Sie das normalisierte Koordinatensystem des Beispielprogramms so, daß die Werte von -1 bis +1 reichen und der Nullpunkt in der Bildschirmmitte liegt. Schauen Sie sich dazu die Formeln in der view_trans-Prozedur an und ändern Sie sie.
In der nächsten Folge werden wir uns mit der dritten Dimension und möglichen Strukturen von Objekten befassen. Es wäre ja langweilig, immer nur das gleiche Haus zu verwenden...

program transform(input, output);
{Programm zum Test von Transformationen mit homogenen Koordinaten}
{----------------------------------------------------------------}
{Das Programm verwendet für alle Berechnungen ein normalisiertes }
{Koordinatensystem, das in beiden Richtungen von 0 bis 1 reicht }
{Vor der Ausgabe werden die Bildpunkte dann in Bildschirmkoordinaten}
{uebersetzt. Zur Anpassung an andere Grafikaufloesungen muss daher }
{fast nichts geaendert werden. }
{----------------------------------------------------------------}
{Dieses Programm wurde mit ALICE geschrieben und für CCD-Pascal }
{angepaßt (Aus Zeitmangel: Nicht schön, aber es läuft). }
{ Achtung: Kein Clipping !!! Die Anpassung der }
{Grafikroutinen an eine andere Ausgabeeinheit ist extrem einfach}
{1. Setzen Sie die Aufloesungswerte ihres Bildschirms oder Grafikfenster}
{bei xmax und ymax ein. Den Abstand der linken unteren Ecke vom absoluten }
{Bildschirmursprung setzen Sie bei xstart und ystart ein. Achtung: die in}
{der Routine View_trans verwendete Formel geht davon aus, dass das System}
{Ihres Bildschirms seinen Ursprung in der linken oberen Ecke hat, wie auf}
{dem ST ueblich.Ist dies nicht der Fall, muss die Formel geaendert werden}
{2. Die Routine do_view benutzt eine procedure line, die Linien von x1,y1}
{zu x2,y2 zieht. Der Aufruf ist der komplette Line-A-Aufruf, die meisten}
{anderen Sprachen bieten einfachere Aufrufe (z.B: Draw(x1,y1,x2,y2) }
{Setzen Sie einfach die entsprechende Funktion ihrer Programier-}
{sprache ein.}
{3. Im Hauptprogramm und an anderen Stellen wird eine Escape-Sequenz }
{ verwendet, um den Bildschirm zu löschen.}
{Auch hier die entsprechende Routine fuer Ihre Sprache einsetzen.}
{------------------------------------------------------------------}
{Auch eine Umsetzung in GfA- oder Omikron-Basic ist kein Problem;}
{Es wurden keine Pascal-Spezialitaeten benutzt.}
{------------------------------------------------------------------}
{ALICE verlangt die Initialisierung aller Variablen vor der ersten}
{Benutzung. In Basic oder anderen Pascal-Dialekten kann auf einige der}
{Initialisierungen (z.B. die Routine init_bild) verzichtet werden}
{------------------------------------------------------------------}
const
xmax = 639; {Diese Zahlen sind die Aufloesung des monochromen}
ymax = 399: {Bildschirms. Hier einfach die Werte}
xstart = 0; {fuer das Zielfenster einsetzen.}
ystart = 399;
type
mat2dh = array {1 .. 3} of array {1..3} of real;
vec2dh = array {1..3} of real;
data = array {1..5} of vec2dh:
var
original : data;
bild : data;
t : mat2dh ; {t ist die Transformationsmatrix}
fenster : text;
g : char;
ende : Boolean;
l_style: integer; {Für CCD-Pascal}
procedure init ;
{Diese Routine oeffnet ein Grafikfenster und leitet alle Grafik-}
{ausgaben dorthin um. Dieses Fenster simuliert dabei den ganzen}
{Atari-Schirm in mittlerer Aufloesung. In der CCD-Version sind}
{diese Befehle auskommentiert. Der Write-Befehl löscht den}
{Bildschirm mit einer Escape-Sequenz}
{und l_style erhält das linienmuster für die line-a-Grafik }
begin
{SetCoordinate(4);}
{Koordinatensystem 640*200. Ursprung oben links}
{page :}
{loescht den Textbildschirm}
{QuickWindow(fenster, 0, 3);}
Write(chr(27),'E');
l_Style: = $FFFF;
end;
procedure init_original ;
{Hier wird ein Bild initialisiert}
begin
original[1][1] := 0.3;
original[1][2] := 0.3;
original[1][3] := 1;
original[2][1] := 0.3;
original[2][2] := 0.6;
original[2][3] := 1;
original[3][1] := 0.5;
original[3][2] := 0.8;
original[3][3] := 1,
original[4][1] := 0.7;
original[4][2] := 0.6;
original[4][3] ;= 1;
original[5][1] := 0.7;
original[5][2] := 0.3;
original[5][3] := 1;
end;
procedure init_bild ;
{initialisierung-s.o.}
begin
bild[1][1] := 1;
bild[1][2] := 1;
bild[1][3] := 1;
bild[2][1] := 1;
bild[2][2] := 1;
bild[2][3] := 1:
bild[3][1] := 1;
bild[3][2] := 1;
bild[3][3] := 1:
bild[4][1] := 1;
bild[4][2] := 1:
bild[4][3] := 1;
bild[5][1] := 1;
bild[5][2] := 1;
bild[5][3] := 1;
end;
procedure ident_mat(var matrix: mat2dh);
{Diese Routine erzeugt eine Einheitsmatrix }
var
i, j : integer;
begin
for i := 1 to 3 do begin
for j := 1 to 3 do begin
if i = j then begin
matrix[i][j] := 1;
end
else begin
matrix[i][j] := 0;
end;
end;
end;
end;
procedure null_mat(var matrix: mat2dh);
{Erzeugt eine Nullmatrix-ist wahrscheinlich nur in ALICE erforderlich}
var
i, j : integer;
begin
for i := 1 to 3 do begin
for j := 1 to 3 do begin
matrix[i][j] := 0;
end;
end;
end;
procedure null_vec(var v: vec2dh);
{Auch hier: Alice verlangt Initialisierung; Nullvektor}
var
i : integer;
begin
for i := 1 to 3 do begin
v[i] := 0;
end;
end;
procedure matmul2dh (m1 , m2: mat2dh; var m3: mat2dh);
{Multipliziert die 3*3 Matrizen m1 und m2; Ergebnis in m3}
var
i, j, k : integer;
begin
for i := 1 to 3 do begin
for k := 1 to 3 do begin
for j := 1 to 3 do begin
m3[i][k] := m3[i][k] + m1[i][j]*m2[j][k];
end;
end;
end;
end:
procedure vecmat2dh(v: vec2dh; m: mat2dh; var w: vec2dh);
{Multipliziert den Vektor v mit der Matrix m, Ergebnis in w}
var
j : integer;
begin
for j := 1 to 3 do begin
w[j] := v[i]*m[i][j] + v[2]*m[2][j] + v[3]*m[3][j];
end;
end;
procedure do_transform(m: mat2dh);
{Multipliziert die Punkte des Originals mit der Transformations-}
{matrix t und verwandelt die homogenen in normale Koordinaten}
var
i, j : integer;
begin
for i := 1 to 5 do begin
vecmat2dh (orig1nal[i], m, bild[i]);
for j := 1 to 2 do begin
bi1d[i][j] := bild[i][j] / bild[i][3];
end;
end;
end;
procedure view_trans(var v: vec2dh; var x1, y1: integer);
{Rechnet die normalisierten Koordinaten (x und y von 0 bis 1) in} {Bildschirmkoordinaten um}
{-----------------------------------------------------------}
{Diese Routine muss zur Anpassung an andere Grafik geaendert werden}
{wenn der Ursprung nicht in der linken oberen Ecke liegt}
begin
x1 := round(v[1]*xmax + xstart);
{Hier werden die Weltkoordinaten in Bildschirmkoordinaten uebersetzt}
y1 := -round(v[2]*ymax - ystart);
{Die Formel fuer y ist so fuer den Nullpunkt in der oberen linken Ecke}
{gedacht. In normalen Systemen analog zur x-Forme! setzen}
end;
procedure do_view;
{Gibt das von do_transform erzeugte Bild auf dem Schirm aus. Benutzt}
{view_trans zur Uebersetzung der normalisierten Koordinaten}
var
i, k : integer;
x1, x2, y1, y2 : integer;
begin
for i := 1 to 5 do begin
if i = 5 then begin
k := -4;
end
else begin
k := 1;
end;
view_trans(bild[i], x1, y1);
view_trans(bild[i + k], x2, y2);
1ine(x1, y1, x2, y2, 1,0,0,0, l_style, 1);
{line zieht eine Linie von x1,y1 zu x2,y2 und muss zur Anpassung}
{durch eine entsprechende Routine ersetzt werden - Hier ist es }
{ein direktes line-a-Binding, deswegen die zusätzlichen Parameter}
end;
end;
procedure set_scale ;
{Eingabe eines Skalierungswertes; dann Berechnung von t}
var
x, y, s : real;
m : mat2dh;
begin
ident_mat(m);
write('scale x:');
readln(x);
m[1][1] := m[1][1]*x;
write('scale y:');
readln(y);
m{2][2] := m{2][2]*y;
write('scale global:');
readln(s);
m[3][3] := m[3][3]*s;
matmul2dh(t, m, t);
end;
procedure set_shear ;
{Eingabe von Verzerrungswerten und Berechnung von t}
var
m : mat2dh;
x, y : real;
begin
ident_mat(m);
write('shear x:');
readln(x);
m[1][2] := m[1][2] + x;
write('shear y:');
readln( y);
m[2][1] := m[2][1] + y;
matmul2dh(t, m, t);
end;
procedure set_trans;
{Verschiebungseingabe und Berechnung von t}
var
m : mat2dh;
x, y : real;
begin
ident_mat(m);
write('trans. x:');
readln( x);
m[3][1] := m[3][1] + x;
write('trans.y:');
readln( y);
m[3][2] := m[3][2] + y;
matmul2dh(t, m, t);
end;
procedure set_rot ;
{Und schliesslich Drehungen; Berechnung von t}
var
m : mat2dh;
a : real;
c, s : real;
n : real;
i : integer;
begin
ident_mat(m);
write('dreh Winkel:');
readln( a);
c := cos(a);
s := sin(a);
for i := 1 to 3 do begin
n := m[i][1]*c - m[i][2]*s;
m[i][1] := m[i][1]*s + m[i][2]*c;
m[i][1] := n;
end;
matmul2dh(t, m, t);
end;
begin
ende := false;
ident_mat(t);
init ;
init_original ;
init_bild ;
{Anzeige des Originalbildes}
do_transform(t);
do_view ;
{In dieser Schleife koennen verschiedene Transformationen ausprobiert}
{werden. Kombinationen sind moeglich - erst ’restart" loescht t}
repeat
write(chr(27),'H'); (Escape-Sequenz für CCD-Pascal-Cursor Home}
writeln('1.scale');
writeln('2.shear');
writeln('3.translate');
writeln('4.rotate');
writeln('5.restart');
writeln('6.quit');
readln(g);
case g of
'1': begin
set_scale ;
end;
'2': begin
set_shear ;
end;
’3': begin
set_trans ;
end;
'4': begin
set_rot ;
end;
'5': begin
ident_mat(t);
Write(chr(27),'E');
{ loescht den Bildschirm - hier also entsprechende }
{Routine aufrufen}
end;
'6': begin
ende := true;
end;
end;
do_transform(t);
do_view ;
until ende = true;
end.