
Bilderspiele: Faszination Computergrafik

Wer hat noch nicht über Musikvideos oder Werbefilme gestaunt, die mit verblüffenden, ja manchmal überraschend realistischen, aber offensichtlich künstlichen Bildern produziert waren? Wer hat noch nie vor Schaufenstern gestanden und die Demografiken der ausgestellten Computer betrachtet? Jedem Manager ist Computergrafik als Business-Grafik bekannt, fast allen Ingenieuren und Architekten ist sie in CAD-Systemen vertraut. Die Flut der erhältlichen Malprogramme für fast alle Computer beweist, wie groß das Interesse an Grafik ist und wieviele Programmierer sich damit auseinandersetzen. Darum wollen wir in dieser Serie versuchen, unseren geschätzten Lesern einen Überblick über die drei großen Ws der Computergrafik zu verschaffen: Das Wofür, das Was und das Wie. Wir hoffen, Ihnen damit einen Einblick in eines der aktivsten Gebiete der modernen Computertechnik zu verschaffen. Die kaum zu überblickenden Aktivitäten in dieser Sparte bringen leider auch eine ungeheure Fülle von Material mit sich, über das berichtet werden soll. Und da wir nicht ausschließlich an der Oberfläche der Techniken bleiben, sondern Ihnen auch einiges an Knowhow vermitteln wollen, wird es leider nicht ohne eine gehörige Portion Mathematik gehen. Auch diese mathematischen Werkzeuge sollen jedoch möglichst verständlich beschrieben werden. Ausführlich werden wir auf wichtige Literatur eingehen, damit auch die interessierten Spezialisten Lösungen für mögliche Probleme finden - denn unsere Serie kann von dem riesigen Gebiet natürlich nur Ausschnitte zeigen.
In dieser ersten Folge wird es zunächst um verschiedene Anwendungsgebiete und die daraus resultierenden, sehr unterschiedlichen Grafiksysteme gehen.
I. Anwendungen der Computergrafik
Es ist keine neue Erkenntnis, daß das Auge von allen menschlichen Sinnen die größte Bandbreite besitzt, also die meisten Informationen innerhalb einer bestimmten Zeit verarbeiten kann. Sehr früh begannen darum die Versuche, auch Ergebnisse von Computerrechnungen grafisch darzustellen. Lange Zeit waren alle Anwendungen in dieser Richtung ausschließlich Großanwendern Vorbehalten, da die Kosten für grafikfähige Peripheriegeräte in astronomischen Höhen lagen. Von der allgemeinen technischen Entwicklung der Computer profitierte aber natürlich auch dieser Anwendungsbereich.
Ein besonderes Beispiel für Anwendungen von Computergrafik, deren Konzept auf der großen Bandbreite des Auges beruht, ist das Xerox-Betriebssystem Smalltalk, das der Urvater fast aller mausorientierten, menügesteuerten Betriebssysteme ist. Man denke etwa an GEM von Digital Research oder an das MacIntosh-Betriebssystem; das Amiga-Konzept ist indes etwas anders. Icons, Fenster, Menüleisten und andere grafische Objekte -all dies sind Versuche, Informationen in leicht erfaßbarer, also grafischer Form auf dem Bildschirm darzustellen.

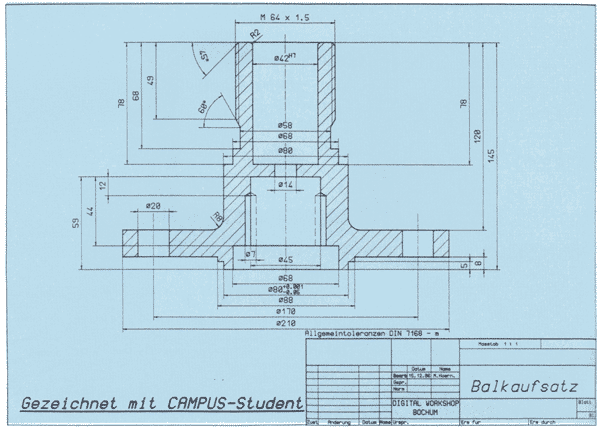
Die 'klassischen’ Anwendungen der Computergrafik sind allerdings CAD-Systeme. CAD ist eine Abkürzung für 'Chip Aided Design’, was etwa ’rechnerunterstützter Entwurf bedeutet. Das ist ein weitreichender Begriff. Es gibt Systeme zum Entwurf der verschiedensten Dinge, von Maschinen bis hin zu VLSI-Schaltungen oder Platinenlayouts. Sinn der Sache ist es, Entwürfe jeder Art zu vereinfachen. Damit soll es möglich sein, technische Zeichnungen maßstabsgetreu mit Computerhilfe zu erstellen und zu modifizieren. Dabei ist der Computer im einfachsten Fall lediglich Zeichenhilfe, also Zeichenbrettersatz. Andere Funktionen, die z. B. automatische Bemaßung erlauben, können hinzukommen. Grosse Systeme können das Gezeichnete auch dreidimensional darstellen und Berechnungen durchführen, die die Funktion der zu entwerfenden Technik betreffen. Ein Schaltungsentwurfssystem kann zum Beispiel vor dem Berechnen des Platinenlayouts eine Schaltungssimulation durchführen. Diese Dinge gehören allerdings nicht in den Bereich der Grafik.
Eine weitere Anwendung, die in der letzten Zeit für professionelle Video-und Grafik-Designer wichtig geworden ist, sind Malprogramme, die auf dem Bildschirm mehr oder weniger gut die traditionellen Werkzeuge des Grafikers simulieren. Im allgemeinen sind solche Programme zusätzlich um sehr leistungsfähige Funktionen erweitert, die ohne Computer kaum realisierbar wären. Haupteinsatzgebiet solcher Programme ist die nachträgliche Bearbeitung digitalisierter Videobilder. Jedem Anwender eines Atari, Amiga oder Macintosh sind derartige Malprogramme wohl ein Begriff. Die professionellen Ausführungen bieten im allgemeinen auch nicht erheblich mehr Funktionen als Deluxe Paint auf dem Amiga oder der Art Director auf dem Atari. Sie arbeiten aber natürlich normalerweise auf Computern, die erheblich höhere Auflösungen und vor allem weitaus mehr Farben (typischerweise zwischen 65 000 und 16 Millionen verschiedene Farbtöne) bieten.
Zwischen diesen beiden Arten von Grafikanwendungen gibt es einen grundlegenden Unterschied, der deshalb so wichtig ist, weil er die gesamte Computergrafik in zwei Welten teilt. CAD-Programme arbeiten objektorientiert, während Malprogramme im Gegensatz dazu pixelorientiert funktionieren. Was bedeuten diese Begriffe? Ein objektorientiertes Grafikprogramm erzeugt, gleichgültig was seine spezielle Aufgabe ist, grafische Objekte, die als solche im Speicher gehalten werden und erst in einem zweiten Arbeitsschritt auf ein grafisches Ausgabemedium (siehe Info-Kasten) ausgegeben werden. Will man zum Beispiel einen Kreis zeichnen, so speichert der Rechner intern die Beschreibung dieses Kreises, also seinen Mittelpunkt und seinen Radius. Eine eigene Zeichenroutine zeichnet diesen Kreis. Weil die Beschreibungen aller grafischen Objekte gespeichert sind, ist es kein Problem, Teile eines Bildes zu verändern. Um z. B. den oben erwähnten Kreis zu ändern, braucht man nur entweder seinen Radius oder seinen Mittelpunkt zu verändern, muß dann aber leider das ganze Bild löschen und alle Objekte neu zeichnen. Das Programm weiß ja nicht, welche Pixel auf dem Bildschirm zu dem Objekt gehören, oder welche anderen Objekte von dieser Änderung betroffen sind. Es wäre auch sehr aufwendig, dies festzustellen. Daher wird bei einer Änderung im allgemeinen das ganze Bild neu aufgebaut. Sollen dreidimensionale Objekte konstruiert werden, ist diese Art der Objektspeicherung unbedingt erforderlich, weil das Objekt, um auf einem zweidimensionalen Bildschirm dargestellt zu werden, erst einmal auf mathematischem Wege auf diesen Bildschirm projiziert werden muß. Im Gegensatz dazu bearbeiten die Funktionen eines Malprogramms direkt die Pixel des Bildschirms. Wenn etwas mit einem Malprogramm dargestellt wurde, kann es nachträglich nicht mehr modifiziert werden, es kann also nicht mehr unabhängig von seinem Hintergrund und seiner näheren Umgebung bearbeitet werden. Das ist wie beim Malen auf einem Stück Papier: Wenn Sie einen Kreis in ein Bild hineinmalen, dann können Sie ihn nur mit einem Radiergummi entfernen - wobei auch der Hintergrund verschwindet. Im Gegensatz dazu entspricht objektorientiertes Arbeiten mehr einer Collagetechnik: Sie fertigen die einzelnen Objekte einzeln an und legen sie in die richtige Anordnung. Jetzt können Sie natürlich einzelne Objekte wieder wegnehmen und verändern, ohne damit die anderen Objekte zu beeinflussen.

Die Anwendung von pixelorientierten Programmen ist daher tatsächlich im wesentlichen auf grafische Arbeit im traditionellen Sinn beschränkt, wenn auch häufig mit zahlreichen zusätzlichen Möglichkeiten. Eine Anwendung ist zum Beispiel die Nachbearbeitung von Videobildern oder von Bildern objektorientierter Systeme. Häufig werden solche Systeme auch zur Titel-und Textgenerierung im Fernsehbereich oder eben tatsächlich als Malprogramm eingesetzt.
In dieser Serie soll es uns aber vor allem um objektorientiertes Arbeiten gehen. Uns soll interessieren, wie man Objekte im Rechner speichert und wie man sie auf dem Bildschirm darstellt. Dann wird die dritte Dimension im Mittelpunkt stehen. Wie bekommt man räumliche Objekte auf den flachen, zweidimensionalen Bildschirm?
Schließlich werden wir uns mit denjenigen Verfahren befassen, die es ermöglichen, mehr oder weniger natürliche Bilder mit dem Computer zu generieren und darzustellen. Licht, Schatten und Farben werden unsere Themen sein. Wie gesagt, all dies erfordert eine Menge Mathematik. Erwarten Sie daher bitte keine abtippfertigen Anwendungsprogramme. Wir möchten Ihnen die mathematischen Verfahren grob erläutern und kleine Beispielalgorithmen angeben. Außerdem werden wir Literatur vorstellen, die Ihnen bei näherem Interesse weiterhelfen kann. Doch nun weiter zum eigentlichen Thema dieses Kapitels: Wofür - außer die rein technisch orientierten CAD-Anwendungen - braucht man Verfahren, die der Generierung natürlich aussehender Bilder imaginärer Welten dienen, und die dazu auch noch Techniken und Geräte erfordern, die ungeheuer teuer sind?

Denken Sie einmal an alle Arten von Simulatoren. Der Versuch, Kosten und Risiken von Testflügen neuer Flugzeugtypen zu vermeiden, führte zur Entwicklung von Flugsimulatoren, die die Bewegungen eines Cockpits recht gut Vortäuschen können und über aufwendige Rechenverfahren auch das Verhalten des geplanten Flugzeuges. Dabei zeigte es sich rasch, daß eine für den Piloten ausreichende Simulation nicht nur künstliche Bewegungen des Cockpits erfordert, sondern auch die Erzeugung einer optischen Reaktion auf die Bewegungen des Flugzeuges, also die halbwegs realistische Simulation einer Landschaft, in der das Flugzeug sich bewegt.
Inzwischen ist man so weit, daß man bei einer simulierten Landung zum Beispiel auf einem Flugzeugträger sogar die Bremsspuren auf dem Deck erkennen kann und die Wellen im umgebenden Ozean oder die Wolken am Himmel erstaunlich realistisch wiedergegeben werden können. Bei solchen Simulationen ist es besonders wichtig, zu beachten, daß die Bilder dabei in Real-Time, für eine halbwegs gute Filmwirkung mit einer Rate von mindestens 20 Bildern pro Sekunde berechnet und dargestellt werden müssen. Eine andere Anwendung sind Filmproduktionen. In dieser Sparte sind auch Musikvideos und Werbefilme enthalten. Hier bieten sich über Computeranimation Spezialeffekte an, die auf diese Weise oft billiger zu erstellen sind als mit den traditionellen Techniken. Ein Beispiel für einen solchen Film ist die Walt-Disney-Produktion „Tron“, bei der der größte Teil des Films komplett vom Computer gezeichnet wurde. Selbst die Kostüme wurden den Darstellern vom Computer auf den Feib gerechnet. Für Animationsfilme mit Computerunterstützung wurden spezielle Animationssprachen und Programmpakete entwickelt. Viele dieser Systeme simulieren die tatsächliche Arbeit einer Kamera: Der Regisseur kann den Kamerastandpunkt ebenso bestimmen wie Blickrichtung, Bildauschnitt, Objektivbrennweite und Szenenbeleuchtung. Kamerafahrten und Bewegungen von Teilobjekten können programmiert werden. Aus diesen Angaben des Regisseurs, die häufig interaktiv an einem einfachen, vom Computer errechneten Drahtmodell eingegeben werden können, werden dann die einzelnen Bilder errechnet.
Architekten können mit computergenerierten Filmen zukünftigen Auftraggebern eine realistischere Vision eines geplanten Gebäudes geben, als dies mit den üblichen Modellbautechniken möglich ist. Selbst einen Rundgang durch das fertiggestellte Gebäude samt Aussicht kann der Computer berechnen. Natürlich ist so etwas sehr aufwendig und heute noch sehr teuer. Die Kosten für derartige Produktionen fallen aber gemeinsam mit den Computerpreisen rasant.
Weitere wichtige Anwendungen für Computergrafik liegen im Business- und Präsentationsbereich. Statistische Daten lassen sich erheblich einprägsamer in grafisch gestalteter Form präsentieren. Die große Arbeit, mit der das Erstellen solcher Grafiken verbunden ist, kann der Computer übernehmen. Schließlich ist auch das in letzter Zeit vielgerühmte Desktop Publishing eine Form der objektorientierten Grafikanwendung. Auch Buchstaben werden dabei als grafische Objekte aufgefaßt und mit Spezialprogrammen für ihre Gestaltung bearbeitet.
II. Was ist machbar? Die Möglichkeiten der Computergrafik
Auch hier ist es wieder notwendig, sich die verschiedenen Arten der Computergrafik bewußt zu machen. Werfen wir zunächst einen Blick auf zweidimensionale Malprogramme: Um hier die Entwicklung zu sehen, genügt es, auf der einen Seite einfache, aber dennoch zu ihrer Zeit revolutionäre Programme wie MacPaint auf dem Macintosh zu betrachten. Diese Programme erlauben es, schnell und problemlos einfache geometrische Formen zu zeichnen und Flächen mit Mustern zu füllen. Außerdem ist es möglich, mit einer simulierten Sprühdose oder verschiedenen Pinseln zu arbeiten und auf dem Bildschirm zu zeichnen wie auf einem Block. Kopieren oder Verschieben von Bildausschnitten ist genauso möglich wie die grafische Darstellung von Text. Neuere Programme, wie zum Beispiel der Art Director auf dem Atari, bieten da einiges mehr. Zum Beispiel kann man Bilder oder Bildausschnitte auf alle denkbaren Arten verzerren, drehen oder spiegeln. Andere Programme erlauben auch die Darstellung von Splines, also beliebig verformbaren Kurven. Zusätzliche Features betreffen die Farbdarstellung und Bearbeitung. Besonders bei den professionellen Programmen, die über große Farbauswahl verfügen, sind diese Möglichkeiten zur Farbbearbeitung ausgeprägt. So gibt es zum Beispiel Pinselmodi, in denen sich der Computerpinsel verhält wie ein Pinsel und Ölfarben; man kann auf diese Weise Farben beliebig verschmieren und malen wie auf Leinwand. Im Grunde sind die Möglichkeiten von Malprogrammen aber wohl ziemlich ausgereizt; die Simulation der klassischen Malwerkzeuge ist inzwischen bei den meisten Programmen recht ausgereift, Erweiterungen bei neueren Programmen enthalten meist nur neue Spezialeffekte, die bei der täglichen Arbeit, wie sie auf dem Profi-Sektor vorkommt, wohl selten benötigt werden. Zum Spielen zu Hause werden diese Features aber immer beliebter.

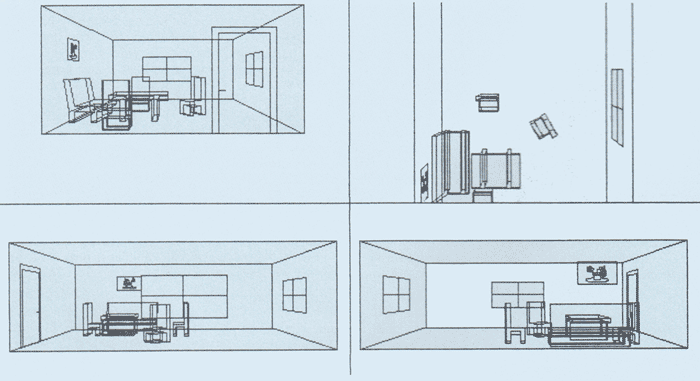
Objektorientierte Zeichenprogramme sind immer stärker 3D-orientiert. Die Zeit, in der sich die Ausgabe der typischen Konstruktionsprogramme im wesentlichen an der Arbeit des technischen Zeichners orientierte, ist im professionellen Bereich längst vorbei. Es werden also nicht nur Pläne von Objekten gezeichnet, der Computer wird auch Werkzeug zur räumlichen Darstellung der konstruierten Objekte und ermöglicht dem Benutzer so eine genauere Vorstellung des Objekts. Dabei ist es wichtig, daß ein Konstruktionsprogramm nicht nur Linien darstellen kann, die die einzelnen Eckpunkte einer Zeichnung verbinden; im Gegenteil, bei der räumlichen Darstellung werden Objekte zumindest aus Flächen, wenn nicht gar aus Volumen zusammengesetzt betrachtet. Wenn ein Körper als Fläche bekannt ist, können Linien, die durch weiter vorne befindliche Objektteile verdeckt werden, ausgeblendet werden; Volumenmodelle erlauben sogar Schnitte durch den Körper. Mit Hilfe der Darstellung von Objekten als räumliche Flächen oder Volumen wird auch die Erzeugung von Licht- und Schatteneffekten auf den Oberflächen des Objektes möglich. Auf diese Art können recht realistische Bilder der konstruierten Objekte erzeugt werden. Einige der dafür erforderlichen Techniken sollen in weiteren Folgen erläutert werden.
Inzwischen ist die Entwicklung so weit, daß selbst mathematisch extrem schwierig zu beschreibende, völlig unregelmäßige Formen wie Wellen oder Wolken realistisch darstellbar sind. Man kann Oberflächenstrukturen von Gegenständen erzeugen und verändern, selbst die Lichtbrechung in transparenten Materialien kann täuschend echt simuliert werden. Die Fortschritte der Computergrafiker sind enorm. Die Verfahren werden immer komplizierter und besser, in höherem Maße, als es die Geschwindigkeit der für die Bilderzeugung notwendigen Rechner vermuten läßt. Auch die Techniken, die für realistische Bilder verwendet werden, wollen wir in dieser Serie ansprechen und beschreiben. Es wird uns allerdings nicht möglich sein, dieses ungeheuer umfangreiche Thema vollständig abzuhandeln. Deswegen sollen im Schluß-Kapitel dieser Folge für besonders Interessierte schon einmal einige wichtige Bücher zur Einarbeitung vorgestellt werden.

III. Nun zur Sache
Leider ist es uns aus Platzgründen unmöglich, hier auf die absoluten Grundlagen der Matrix- und Vektorrechnung und ihrer graphischen Interpretatation einzugehen. Wer sich jedoch darüber genau informieren möchte, dem seien nachdrücklich die Bücher 'Graphische Datenverarbeitung’ oder ’Mathematical Elements for Computer Graphics’ empfohlen. Näheres über beide Bücher im nächsten Kapitel.
Als Beispiel stellen wir uns zunächst einen Kubus vor, der irgendwo im Raum herumschwebt. Dieser Kubus läßt sich jetzt beschreiben:
- Durch seine Eckpunkte.
- Durch Nennung der Eckpunkte, die durch Linien verbunden sind.
- Falls der Kubus massiv sein soll, müssen auch noch die Linien oder Ecken, die die Flächen umschließen, genannt werden.
- Falls die Flächen eine Struktur haben oder auf andere Weise realistisch aussehen sollen, müssen noch andere Daten zusätzlich zur Verfügung stehen, z. B. Brechungsindizes usw. der Oberfläche.
Im Moment sollen uns allerdings nur die Eckpunkte interessieren. Denn es ist offensichtlich, daß nur die Position dieser Punkte im Raum Aussehen und Lage des Kubus bestimmt (alle anderen Angaben sind auf die Position dieser Punkte bezogen, eine Linie kann ja in der Art 'von Punkt A nach Punkt B’ beschrieben werden.
Was könnte man mit einem Kubus im Raum, also mit seinen Eckpunkten, tun? Zuerst einmal könnte man den ganzen Kubus durch den Raum bewegen, entweder entlang einer Linie oder auch um einen Punkt rotierend. Weiterhin könnte man den Kubus vergrößern und verkleinern, entweder insgesamt oder teilweise. 'Teilweise’ soll in diesem Zusammenhang heißen, daß nur ein Teil der Koordinaten der Punkte verändert wird. Aus einem Kubus könnte also ein Schuhkarton werden oder etwas noch viel flacheres. Zuletzt könnte man natürlich noch jeden Punkt des Kubus einzeln bearbeiten. Dabei würde natürlich etwas herauskommen, was nicht mehr sehr viel mit einem Kubus zu tun hätte. Nur eines fehlt noch: Um den Kubus anzuschauen, wenn wir ihn zum Beispiel im Speicher eines Rechners haben, müssen wir einen Weg finden, den Kubus zweidimensional zu machen - leider gibt es ja noch keine 3D-Bildschirme. Der Kubus muß also auf eine Fläche projiziert werden.
Alle diese Operationen haben den grossen Vorteil, daß sie sich mit einer einzigen mathematischen Methode elegant erledigen lassen: Es sind nämlich ausnahmslos Koordinatentransformationen. Um die Möglichkeiten solcher Transformationen und ihre Ausführung zu erklären, gehen wir erst einmal einen Schritt zurück, nämlich ins Zweidimensionale.
Alle aufgeführten Operationen haben gemeinsam, daß sie sich als lineares Gleichungssystem schreiben lassen. Ein solches lineares Gleichungssystem läßt sich auf einfache Weise mit einer Matrix schreiben. In dieser Matrix haben nun verschiedene Elemente ganz einfache geometrische Auswirkungen. Für jede der oben angeführten Operationen gibt es ein Element in der Matrix, das genau die gewünschten Auswirkungen hat, und es ist möglich, mit dem Produkt mehrerer Matrizen beliebig komplexe Transformationen in einem Rutsch durchzuführen. Mehr soll in dieser ersten Folge noch nicht verraten werden; in der nächsten Folge werden wir solche Matrizen genauer betrachten.
So vielseitig eine Matrix ist, es gibt auch Probleme der Computergrafik, die nicht mit einfachen Matrixoperationen gelöst werden können. Denken Sie noch einmal an den Kubus im Raum. Wenn Sie irgendeinen Schuhkarton betrachten, wird Ihnen auffallen, daß Sie nicht alle Flächen und Kanten des Kartons gleichzeitig sehen können. Natürlich nicht, die hinteren Teile werden ja durch die vorderen verdeckt. Dummerweise ist es gar nicht so einfach, festzustellen, welche Teile eines Objektes für einen Betrachter von einer bestimmten Position aus verdeckt sind. Um diese Teile zu finden und bei Bedarf auszublenden, sind weitaus komplexere Verfahren notwendig, die auch nicht mehr rein mathematischer, sondern eher algorithmischer Struktur sind. Aber auch hiermit werden wir uns noch befassen.
IV. Literatur
Gute und billige Einführungen und Lehrbücher gibt es im Verlag McGraw-Hill. Vier Bücher aus diesem Verlag seien besonders empfohlen: Wer eine allgemeine Einführung wünscht, die sich nicht allzusehr an mathematischen Details festhält, dafür aber umfassend informiert, sollte sich 'Prinzipien der interaktiven Computergrafik’ von Newman/Sproull näher ansehen. In diesem Buch, das sogar in deutscher Übersetzung vorliegt, findet man fast alles, was das Grafik-Herz begehrt - nur leider nicht die Details und mathematischen Methoden, die man selbst zum Programmieren braucht.
Doch diese Lücke füllen drei andere Bücher aus dem gleichen Verlag vollständig. Die wichtigsten mathematischen Grundlagen der Computergrafik enthält 'Mathematical Elements for Computer Graphics’ von David F. Rogers und J. Alan Adams. Leider ist dieses sehr empfehlenswerte Buch nur auf Englisch erhältlich. Es enthält aber, relativ verständlich formuliert, alle wichtigen mathematischen Werkzeuge, die für Computergrafik benötigt werden. Wichtig ist dabei vor allem, daß die Darstellung einheitlich und konsequent ist; man muß sich also nicht immer wieder an neue Schreibweisen gewöhnen, was fast unumgänglich ist, wenn man sich den Inhalt dieses Buches aus verschiedenen anderen Darstellungen zusammensuchen muß.
Wie bereits im letzten Abschnitt erwähnt, es gibt eine ganze Reihe von Problemen (sozusagen die höhere Schule der Computergrafik), die algorithmische Lösungsverfahren erfordern. Eine großangelegte Sammlung wichtiger Algorithmen gibt David F. Rogers in seinem zweiten Grafikbuch ’Procedural Elements for Computer Graphics’. Dieser Band erfordert allerdings schon recht ausführliche Kenntnisse in Vektor- und Matrixrechnung. Jedem, der sich wirklich intensiv mit der Materie beschäftigen will, sei er jedoch empfohlen.
Wer vor allem an praktischen Problemlösungen interessiert ist und von Theorie nur das unbedingt notwendige Mindestmaß wissen möchte, findet in dem Buch 'Computer Graphics -A Programming Approach’ von Steven Harrington (auch dieses Buch ist leider nur Englisch erhältlich) einen systematischen Kurs, in dessen Verlauf eine komplette 3D-Grafik-Bibliothek programmiert wird. Die notwendige Mathematik wird recht gut erklärt, man kann also sehr gut verstehen, was in den einzelnen Modulen passiert. Vor allem ist keine intelligente Grafikhardware notwendig. Begonnen wird in dem Buch mit Routinen zum Linienziehen, Mindestvoraussetzung ist also lediglich ein Terminal oder Drucker mit positionierbarem Cursor bzw. eine Funktion, mit der sich ein Bildschirmpunkt löschen oder setzen läßt. Alle Algorithmen sind in einer Pseudosprache geschrieben, die sich leicht in Pascal, Modula II oder GFA-Basic oder jede andere Sprache, die Prozeduraufrufe zuläßt, übersetzen läßt.
Im Hanser-Verlag gibt es ein Buch mit dem Titel 'Grafische Datenverarbeitung’ (von Ian O. Angell). Wer eine Einführung in Mathematik und Algorithmen sucht und kein Englisch kann, ist mit diesem Buch sicher sehr gut beraten. Die Erklärungen sind gut verständlich, allerdings sind die Prograrrtm-beispiele in Fortran geschrieben, so daß Vorkenntnisse in dieser Sprache geraten scheinen.
Im Springer-Verlag Berlin (nicht Axel) erscheinen Serien von Büchern, die sich mit den Fortschritten und Entwicklungen der Computergrafik beschäftigen. Ein solches, zweibändiges Werk sei hier herausgegriffen: Serie ’Eurographic Seminars’, ’Advances in Computer Graphics’, herausgegeben von G. Enderle, M. Grave und F. Lillehagen. Eine ganze Reihe von Autoren berichtet hier in ausführlichen Aufsätzen über neue Entwicklungen der Computergrafik. Außerdem enthält der erste Band sehr gute Zusammenfassungen von Grundlagenwissen. Die Beiträge sind in Englisch, allerdings ist auch ein französischer Artikel von kanadischen Autoren darunter. Besonders interessant an diesen Bücherserien von Springer ist, daß sie einen Einblick in aktuelle Themen und Entwicklungen geben, der in Zeitungsartikeln in dieser Ausführlichkeit nicht möglich ist. Leider sind diese Bücher auch sehr teuer. So, das war’s für diese Folge. In einer der nächsten Ausgaben geht es dann weiter. Wer Lust hat: Unbedingt mit Vektoren und Matrizen beschäftigen, es lohnt sich! (CS)
Info-Kasten 1
Es gibt sehr unterschiedliche grafische Ausgabemedien, zum Beispiel Drucker, Plotter oder Bildschirme. Dabei gibt es zwei Typen von Geräten: Raster- und vektororientierte.
Rasterorientierte Geräte bauen ihr Bild aus einzelnen Punkten auf, vektororientierte Geräte aus Linien. Ein Matrixdrucker muß zum Beispiel eine schräge Linie aus einzelnen Punkten zusammenbauen, was zu Treppchen führt. Ein Plotter dagegen kann direkt eine schräge Linie zeichnen. Rasterorientierte Systeme haben den Vorteil, daß es erheblich einfacher ist, flächige Bilder zu erzeugen.
Auch bei Bildschirmen gibt es vektororientierte Geräte. Diese haben für die Computergrafik aber nicht mehr die Bedeutung, die heute Rasterbildschirme haben. Daher werden wir uns in dieser Serie auf rasterorientierte Ausgabegeräte beschränken. Alle Verfahren, die wir beschreiben, können daher ohne Probleme auf Matrixdruckern oder 'normalen* Computerbildschirmen verwendet werden.