
Fractals IV - Fraktale Zeiten
Um uns herum regiert das Chaos! Damit wir uns recht verstehen, hier verbreitet keiner Endzeitstimmung oder käut Stammtischparolen über Politik und Wirtschaft wieder. Vielmehr ist hier die Rede von der Faszination des mathematischen Chaos. Auch ohne theoretisches Grundwissen zaubern Sie mit Fractals IV Apfelmännchen, Juliamengen, Biomorphe und Hüpfer-Diagramme von atemberaubender Schönheit.
Nicht schon wieder", so stöhnen jetzt einige Leser. „Apfelmännchengeneratoren in allen Variationen überschwemmen nun doch wirklich den Markt." Das mag stimmen, allerdings vermag Fractals IV von Harald & Martin Hansen erheblich mehr, als nur langsam Mandelbrotmengen zu berechnen. Daß in dem Programm mehr steckt, zeigt allein schon das knapp einhundertseitige Handbuch, in dem auch Nichtmathematiker die wichtigsten Grundlagen und Formeln für die Berechnung des Chaos finden.
Hardwarepower? Ja und nein!
Fractals in der Version 4.30 berechnet auf jedem beliebigen ATARI-Rechner die auch als Apfelmännchen bekannten Mandelbrot- und Juliamengen. Daneben lassen sich auch Biomorphe, eine Art Abkömmling der Mandelbrotmengen, und neuerdings auch Hüpfer-Diagramme ausgeben. Der Fraktalgenerator unterstützt jede Monitorauflösung ab 640 x 400 Bildpunkte. Das heißt, neben der monochromen Darstellung benötigen Sie für die maximal 256 Farben entweder die hohe TT-Auflösung, die VGA-Standardauflösung des Falcon oder eine Grafikkarte. Mit diesen Erweiterungen verträgt sich der fraktale Zauberer übrigens aufgrund seiner sauberen GEM-Programmierung hervorragend. Damit Sie auch die niedrigeren Auflösungen der kleinen ST(E)s nutzen können, empfehlen die Programmautoren den Einsatz von Julian Reschkes „Big-Screen 2.0".
Natürlich erfordern die komplexen Berechnungen jede Menge Rechen-Power. Der 68030-Prozessor eines TT und ein mathematischer Coprozessor sind durchaus empfehlenswert und für einige Iterationsformeln unabdingbar. Wer ohne diese Rechenkünstler auskommen muß, braucht jedoch nicht zu verzweifeln. Fractals verfügt in diesem Falle über optimierte Assembler-Codes, die einen Großteil der Formeln trotzdem in annehmbarer Zeit durchlaufen lassen. Es mag an dieser Stelle gleich erwähnt sein, das Fractals IV auch im Multitasking-Betrieb arbeitet, wenn auch mit kleinen Einschränkungen. Ob dies aufgrund der äußerst rechenintensiven Abläufe sinnvoll ist, muß jeder Anwender selbst entscheiden.
Bevor das Programm jetzt seine Muskeln spielen läßt, noch ein paar grundsätzliche Anmerkungen für diejenigen, die mit Begriffen wie Fraktale, Chaos und dergleichen nichts anfangen können. Wie schon eingangs bemerkt, herrscht in unserer Umgebung das Chaos und das Unberechenbare. Wenn Sie nun meinen, mit Ihrem Computer oder noch leistungsfähigeren Geräten lasse sich alles und jedes exakt berechnen, dann irren Sie sich. Versuchen Sie nur einmal, den Verlauf eines Wassertropfens auf einer senkrechten Glasscheibe oder die Fallrichtung der Schneeflocken exakt vorherzusagen. Selbst unter Laborbedingungen, mit standardisierten Voraussetzungen, erhalten Sie nie ein gleiches Ergebnis. Kaum spürbare Einflüsse, die nicht vorhersehbar sind, beeinflussen alle Abläufe, also zum Beispiel den Verlauf des Regentropfens auf der Fensterscheibe. Der Mensch wäre nicht Mensch, wenn er nicht trotzdem versuchen wollte, diese Unwägbarkeiten mit Formeln und Theorien in den Griff zu kriegen. Wie schwierig zu erhalten und wie ungenau das Ergebnis sein kann, führt Ihnen die allabendliche Wetterkarte vor.
Die Grundlage all dieser Theorien bildet die fraktale Mathematik mit ihren komplexen Zahlen. Ich will Sie jetzt nicht mit der Auflistung undHerleitung solcher Zahlenreihen langweilen; wer es genauer nachlesen will, kann sich das Kapitel „Mathematische Grundlagen" im Fractals-IV-Handbuch anschauen. Mit der Untersuch-nung von komplexen Zahlen und deren Anwendung beschäftigen sich viele Mathematiker, so auch vor 70 Jahren der Franzose Gaston Julia oder 50 Jahre später Benoit Mandelbrot. Deren mühseliege Berechnungen ohne Computer spiegeln sich heute in den fraktalen Grafiken wider. Kehren wir zurück zu Fractals IV. Um an eines dieser phantasie vollen Gebilde zu gelangen, stehen Ihnen mehrere Möglichkeiten offen. Die simpelste Methode: Sie laden von der Bilder-Disk bereits ein fertig berechnetes Fraktal, ändern eventuell einzelne Parameter und starten die Neuberechnung. Sie verändern nur die einzelnen Farbwerte, laden eine zusätzliche Farbtabelle oder geben in der monochromen Darstellung das Bild mit maximal 64 Graustufen aus.
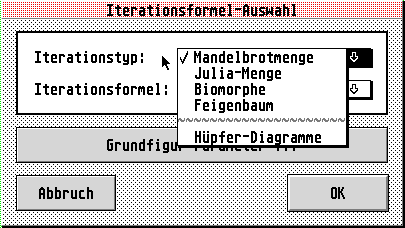
Oder Sie wählen eine der über 20 verschiedenen Iterationsformeln und einen der vier Iterationstypen, also beispielsweise die Juliamengen, aus. Neben der bekannten Apfelmännchenformel „z2+c" finden Sie auch komplexere, wie zum Beispiel „cos(z)*c", deren Berechnung, vor allem in Farbe, sich auch schon mal über Stunden hinzieht. Wie bei fast allen Einstellungen und Menüvorgaben verwendet der Generator auch hierfür modale Fensterdialoge. Weitere Menüebenen erreichen Sie dann entweder über Pop-Up-Menüs innerhalb der Dialoge oder über ein weiteres Dialogfenster. Die klare Gliederung und Übersichtlichkeit der Programmführung ist dabei eine gute Hilfe. Zusätzlich legen Sie alle wichtigen Bildparameter der Grundfiguren fest. Das sind Bildkoordinaten und -große und die Anzahl der Rechendurchläufe. Ein Klick auf den Menüpunkt „Iteration/Grundfigur" startet dann die Berechnung des Fraktals.
Tor zur neuen Welt
Während der Berechnung baut sich im Grafikfenster allmählich das Fraktal auf. Das heißt, bei einigen Formeln sehen Sie eine ganze Zeitlang überhaupt nichts, da sich der Computer erst schwindelig rechnet, bevor er die ersten Zeilen des Bildes ausgibt. Wesentlichen Einfluß auf Rechenzeit und Darstellung hat unter anderem die Wahl des „Interpolationsverfahrens". Der Clou bei der Interpolation ist, daß der Rechner nicht mehr jeden einzelnen Bildpunkt eines Fraktals berechnet. Mit Hilfe ausgeklügelter Verfahren vergleicht Frac-tals die Färb- und Tiefenwerte benachbarter Pixel und fügt einen geschätzten Mittelwert ein. Diese Methode beschleunigt den Rechenvorgang, führt jedoch zu kleinen, vernachlässigbaren Fehlern. Stellen Sie die Interpolation aus, dann erhalten Sie ein fehlerfreies Ergebnis, müssen aber unter Umständen mal eine Nacht auf das Ergebnis waren. Besser ist es, die Interpolation beizubehalten und zwischen Punkt-, Zeilen- oder Flächeninterpolation zu wählen. Diese Modi bestimmen im Prinzip, nach welchen Gesetzmäßigkeiten Bildpunkte berechnet (iteriert) oder geschätzt (interpoliert) werden, und beeinflussen somit das Arbeitstempo.
Das fertige Kunstwerk sollten Sie vor der weiteren Bearbeitung erst in einen der 20 Bildspeicher ablegen. Der Name des Bildes erscheint dann in der Funktionsleiste am unteren Bildschirmrand und läßt sich jederzeit durch einen Mausklick wieder anzeigen. Möchten Sie dem Fraktal so richtig auf den Grund gehen, dann zoomen Sie sich in die Tiefe. In einem Dialog geben Sie alphanumerisch die neuen Bild-koordinalten ein, beziehungsweise Sie makieren mit der Maus den gewünschten Ausschnitt. Falls nötig, passen Sie die Bildausmaße nochmals an, bestimmen die neue Rechentiefe und bringen anschließend CPU und FPU zum Rauchen. Wer will, kann auch Bildfamilien anlegen, bei denen eine Verkettung von Ursprungsbild und nachfolgenden Zoomausschnitten zu einer Bildfolge führen. Hierfür ist eine komfortable Bildfamilienverwaltung vorhanden. Übrigens stoppen Sie die Berechnung eines Fraktals jederzeit durch den Druck auf „ESC". Der Generator rechnet in diesem Fall die jeweilige Bildzeile zu Ende. Eine Fortsetzung der Iteration zu einem späteren Zeitpunkt ist dann kein Problem. Vorausgesetzt, Sie speichern den Tiefenwert des Fraktals. Dieser Wert enthält unter anderem die Anzahl der Rechenschritte mit den zugeordneten Farbwerten.
Film ab!
Ausführliche Informationen über ein Fraktal, wie Bildparameter, Iterationsmodus und -zeit, Rechentiefe, erhalten Sie mit Bild-Info. Anstatt hierfür die Menüleiste zu bemühen, reicht auch ein Mausklick in das Fenster, und ein Pop-Up mit den wichtigsten Funktionen erscheint. Natürlich lassen sich auch explizit Werte eingeben, beispielsweise, um ein fertiges Fraktal neu zu berechnen oder um Formeln und Werte aus anderen Quellen zu verwenden. Mögliche Fehler bei der Eingabe meldet Fractals sofort. Zudem erlaubt das Programm die Definition einer speziellen Bildfolge. Sie definieren, passend zum aktuellen Bild, ein sogenanntes Zielbild. Das ist ein gezoomter Ausschnitt oder ein, den Koordinaten und dem Iterationstyp entsprechendes, bereits fertiges Fraktal. Das Programm berechnet daraufhin bis zu 4095 (!) einzelne Zwischenbilder. Lassen Sie doch einmal die fertige Bilderfolge mit dem beiliegenden Tool „Fractalshow" als Filmsequenz abspielen. Ich verspreche Ihnen einen atemberaubenden Flug in bis dato unbekannte Welten. Insbesondere die bizarren Biomorphe und Juliamengen geben dafür jede Menge Stoff her. Allerdings geht es bei der Kino Vorführung schon hart an die Ressourcen des Rechners und Anwenders.
Mandelbrot- und Juliamenge einmal bildlich gesehen
Kommen wir noch einmal zurück auf die schon erwähnte Tiefenwert-Datei. Mit ihrer Hilfe hält Fractals IV noch ein paar äußerst interessante Spielereien bereit. Im unteren Teil des Menüs „Iteration" finden Sie einige Funktion zur nachträglichen Bearbeitung eines Fraktals. Die schon eingangs erwähnte Graustufenrasterung erlaubt die unterschiedliche Zuordnung von Graurastern und Tiefen werten. Am besten, Sie probieren einmal die verschiedenen Einstellungen: Sägezahn, Dreieck, Sinus und Wurzel aus. Verschiedene Start-und Endwerte geben zusätzliche Gestaltungsmöglichkeiten. Fünf Seiten Graustufenbehandlung im Handbuch geben den „monochromen ATARIanern" genügend Tips für kreative Eigenschöpfungen. Was dem einen die Grauraster, das sind dem anderen die Farbeinstellungen. Auch hier lohnt sich das Experimentieren. Nicht nur einfaches Tauschen von Paletten, sondern auch Neuverteilen von Farbwerten oder Umfärben von Schwarzweiß in Farbe gehört hier zu den Pflichtübungen. Jedem Bild des Bildspeiches läßt sich, nebenbei bemerkt, eine eigene, lokale Farbpalette zuordnen. Den Statistikern unter den frakta-len Freaks gibt das Verteilungsdiagramm der Tiefen werte genaueren Aufschluß über die Struktur des Fraktals. Sie erhalten unter anderem genaue Informationen über das Verhältnis von Tiefenwert und Graustufen-/Farbzuordnung .
Ganz neue Perspektiven
Ein ganz unerwartetes Feature ist die dreidimensionale Darstellung eines Fraktals. Sie bestimmen Dreh- und Neigungswinkel, Bildgröße und die Überhöhung des Fraktals in der räumlichen Projektion. Natürlich erhalten Sie das Ganze wieder als S/W-, Graustufen- oder Farbdarstellung. Vielfältig wie alle Funktionen sind auch die Möglichkeiten der Druckausgabe. Wie es sich für ein ordentliches GEM-Programm gehört, unterstützt Fractals die Ausgabe via GDOS. Da das aber, besonders für Neulinge, nicht ganz unproblematisch ist, besteht noch eine weitere Möglichkeit. Die Druckroutinen unterstützen grundsätzlich alle EPSON-FX-kompatiblen 9-Nadler, die 24-Nadler mit NEC-P6-Emulation und schließlich alle HP-Laser-Kompatiblen. Die genaue Konfiguration müssen Sie über hexadezimale Druckercodes vornehmen. HP-500C- und 550-C-Besitzer gelangen in den Genuß eines farbigen(!) Auszuges. Gewissermaßen als Entschädigung läßt sich die S/W-Kopie auch in Graustufen umrechnen. Wer qualitativ hochwertige Ausgaben in Händen halten möchte und über ausreichend Geduld verfügt, probiert die Superformat-Option. In diesem Falle iteriert Fractals die Bilder direkt für den Druck und sorgt damit für eine optimale Auflösung.
Was bleibt...
... ist ein bekehrter Tester. Bislang hatte ich bei Apfelmännchen & Co allenfalls ungute Erinnerungen an den Matheunterricht. Fractals IV ist jedoch der ideale Grund, sich näher mit der Materie zu beschäftigen. Wer Spaß am Experimentieren hat und die höhere Mathematik kunstgerecht aufbereiten möchte, sollte die 69 Mark für Fractals IV ausgeben.
Bezugsquelle: Hansen Software Steinkopfstraße 22 6J169 Friedberg
Fractals IV
Positiv:
einfache Handhabung
Vielzahl von Iterationsformeln und -typen
tolle Ergebnisse
umfangreiche Nachbearbeitung möglich
Negativ:
etwas komplizierte Druckfunktion
Andreas Wischerhoff